Miroirs
Le miroir primaire est le ... premier miroir vu par les photons. Il présente généralement un profil parabolique. Le deuxième, s'il y en a un, est appelé ... secondaire.

Miroir de 8.2 m poli par la société SAGEM/REOSC, pour le télescope VLT de l'ESO.
Crédit :
REOSC
Miroirs segmentés
Les 2 télescopes Keck,
plus grands collecteurs dans le visible depuis le début des années 1990, ont des miroirs segmentés (càd en plusieurs morceaux), et illuminent les foyers Cassegrain
et Nasmyth. Ce dernier, après passage du faisceau sur l'axe en altitude, est découplé du télescope.
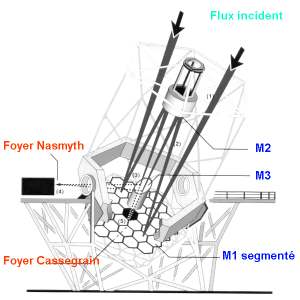
Miroir segmenté, foyers Cassegrain et Nasmyth d'un des 2 télescopes Keck.
Crédit :
Keck
Domaines visible, UV et IR
Une configuration classique est la combinaison de 2 miroirs, l'un parabolique, l'autre hyperbolique convexe, dans la configuration Cassegrain.
Les miroirs ne sont plus nécessairement monoblocs ; c'est le cas du télescope optique le plus grand en service actuellement, le télescope Keck.
Domaine radio
Dans le domaine radio, il est nécessaire d'avoir une antenne de grande taille :
- Pour collecter un grand nombre de photons, car l'énergie
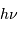 par photon est très faible dans le domaine radio.
par photon est très faible dans le domaine radio. - Afin d'améliorer la fonction de transfert, très étalée par la diffraction à grande longueur d'onde
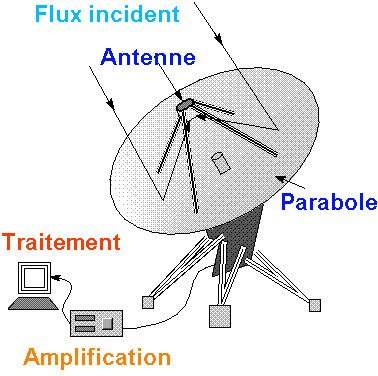
Les éléments de collecte du signal d'un radiotélescope.
Crédit :
ASM
Domaine X
Le domaine des courtes longueurs d'onde présente de nombreuses particularités. Entre autres :
- Seules les observations dans l'espace sont possibles, l'atmosphère étant opaque aux rayonnements X et
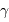 .
. - Il est difficile de focaliser efficacement un rayonnement très énergétique. Pour y parvenir, les miroirs des collecteurs X travaillent en incidence rasante.
- L'imagerie X nécessite un grand nombre de surfaces collectrices.

Télescope XMM de l'agence spatiale européenne, lancé fin 1999 pour une mission de 6 ans.
Crédit :
ESA

Télescope X : principe. Pour assurer un bon coefficient de réflexion dans ce domaine de longueur d'onde, les miroirs sont attaqués en incidence rasante.
Crédit :
ESA

Paraboloïdes chargés de recueillir le flux X en incidence quasi rasante ; 58 paires de paraboloïdes et hyperboloïdes associés assurent les possibilités d'imagerie du collecteur du satellite XMM.
Crédit :
ESA
 Prérequis
Prérequis
Optique géométrique. Formation d'image au foyer primaire d'un télescope.
 Objectifs
Objectifs
Quelques notions sur les collecteurs de photons en astronomie.
Voir à l'infini
Le signal d'un objet très lointain, non résolu spatialement, est une onde plane. Observer cette onde plane, c'est la focaliser en un point. Une surface mathématique sait faire cette opération : le paraboloïde de révolution
(révolution d'une parabole autour de son axe).
La parabole
Mathématiquement, la parabole conjugue l'infini à un point ; optiquement, elle permet de transformer une onde plane en onde sphérique.
Ceci n'est rigoureusement vrai que pour un rayon parallèle à l'axe optique. L'aberration de sphéricité apparaît pour les rayons inclinés sur l'axe.
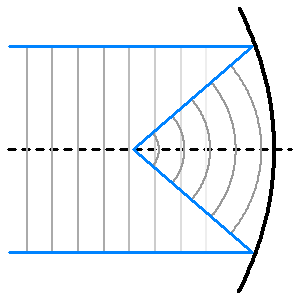
La parabole conjugue l'infini à un point, le foyer. Elle transforme une onde plane en onde sphérique.
Crédit :
ASM

Aberration de sphéricité pour tout objet paraxial, avec un collecteur parabolique.
Crédit :
ASM
Propriétés
Les lois de l'optique permettent de caractériser les qualités de la collecte.


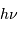 par photon est très faible dans le domaine radio.
par photon est très faible dans le domaine radio.
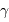 .
.



