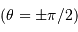 ou à l'équateur
ou à l'équateur 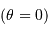 valent respectivement :
valent respectivement :
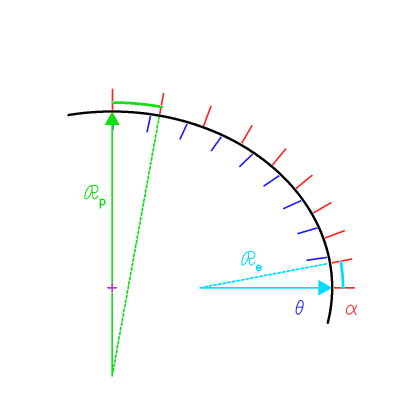
Les rayons de courbures aux pôles 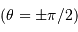 ou à l'équateur
ou à l'équateur  valent respectivement :
valent respectivement :
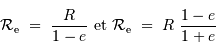
Avec l'hypothèse que 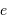 est petit, et les développements limités usuels, on trouve :
est petit, et les développements limités usuels, on trouve :
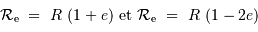
On en déduit que la différence relative des mesures, de l'ordre de 1.2%, correspond à 3 fois le paramètre 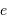 . En effet :
. En effet :
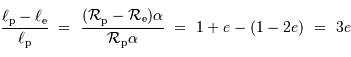
d'où l'aplatissement de la Terre, de l'ordre de 0.4%, cad 1/250.