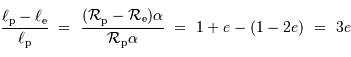Quelle référence pour les coordonnées angulaires ?
Les coordonnées polaires, c'est simple a priori. Sauf que faire les mesures à partir de la surface de la Terre, et non du centre, change le point de vue.
La Terre n'étant pas ronde, la définition des coordonnées angulaires par rapport à la verticale locale ne coincide pas avec une définition centrale.
Coordonnées géographique et géocentrique
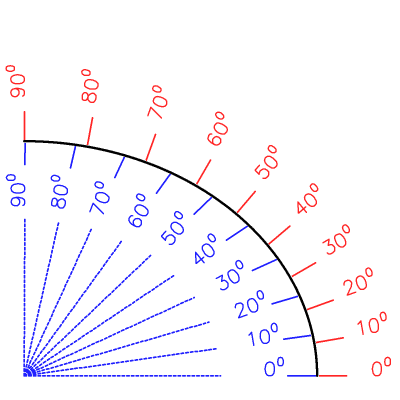
Double définition possible des coordonnées angulaires à la surface d'un objet en forme d'ellipsoïde aplati (tel que la Terre). Les coordonnées géocentriques (bleu) sont définies par rapport au centre de l'objet ; les coordonnées géographiques (rouge) par rapport à la verticale locale.
Crédit :
ASM
 La figure de la Terre
La figure de la Terre
Difficulté : ☆☆
Temps : 30 min
Au milieu du XVIIIe siècle, les missions de La Condamine au Pérou et de Maupertuis au Laponie ont conduit à la mesure de la longueur d'un degré du méridien en Laponie (aux alentours de la latitude 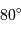 ) ainsi qu'au Pérou (vers
) ainsi qu'au Pérou (vers 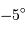 ). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
Question 1)
Expliquer pourquoi la longueur d'un degré le long du méridien diffère entre ces 2 régions. Faire un schéma.
Réfléchir au système de coordonnées utilisé.
Question 2)
La Terre étant aplatie aux pôles, le rayon de courbure local est-il plus important au pôle ou à l'équateur ? Quel degré de méridien correspond à la plus grande longueur ?
Voir la figure de la question précédente.
Question 3)
La longueur 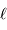 d'un arc de méridien d'ouverture
d'un arc de méridien d'ouverture 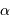 s'écrit en fonction du rayon de courbure
s'écrit en fonction du rayon de courbure 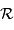 :
:
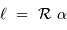
En représentation paramétrique, on repère un point de l'ellipse de révolution par
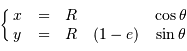
avec 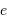 le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en
le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en 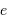 :
:
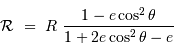
[on peut retrouver ce résultat en appliquant la définition : 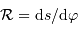 , avec
, avec 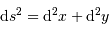 et
et 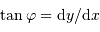 ].
].
Les mesures pour tourner de 1 degré donnant respectivement 57395 toises en Laponie, et 56735 toises au Pérou (57097 au sud de Paris), en déduire
un ordre de grandeur de l'aplatissement de la Terre, exprimé comme la différence relative entre les rayons au pôle et à l'équateur.
Identifier 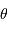 au pôle et à l'équateur, et y calculer
au pôle et à l'équateur, et y calculer 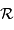 .
.
- Question 1
Aide :
Réfléchir au système de coordonnées utilisé.
Solution :
Les mesures sont effectuées en coordonnées géographiques, les observateurs pouvant p.ex. s'appuyer sur la verticale locale, et non sur une hypothétique et inconnue direction pointant le centre de la Terre.
En raison de la non sphéricité, le rayon de courbure local varie, et donc la mesure d'un arc d'ouverture fixée.
Angles de position géocentrique en bleu, géographique en rouge, repérés pour une équidistance de 10 degrés
Crédit :
ASM
- Question 2
Aide :
Voir la figure de la question précédente.
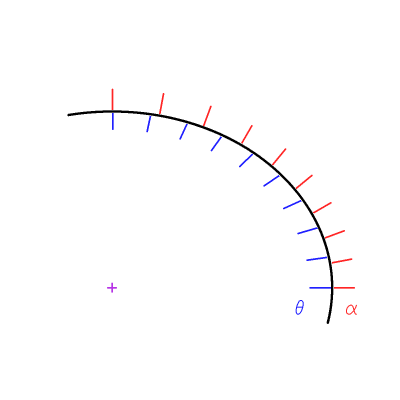
Solution :
Comme le rayon de courbure local est plus important au pôle, une rotation d'un angle géographique de 10 degré sera plus importante au pôle.
Crédit :
ASM
- Question 3
Aide :
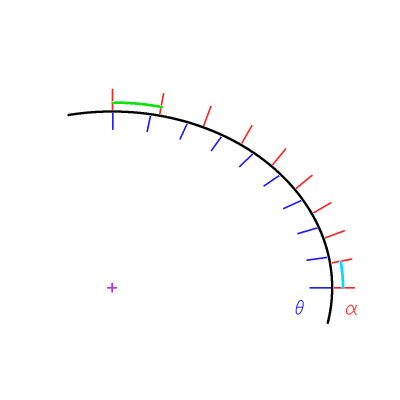
Identifier 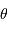 au pôle et à l'équateur, et y calculer
au pôle et à l'équateur, et y calculer 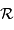 .
.
Solution :
Les rayons de courbures aux pôles 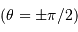 ou à l'équateur
ou à l'équateur 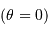 valent respectivement :
valent respectivement :
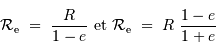
Avec l'hypothèse que 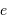 est petit, et les développements limités usuels, on trouve :
est petit, et les développements limités usuels, on trouve :
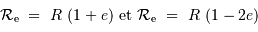
On en déduit que la différence relative des mesures, de l'ordre de 1.2%, correspond à 3 fois le paramètre 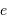 . En effet :
. En effet :
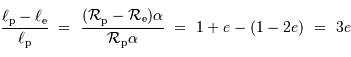
d'où l'aplatissement de la Terre, de l'ordre de 0.4%, cad 1/250.
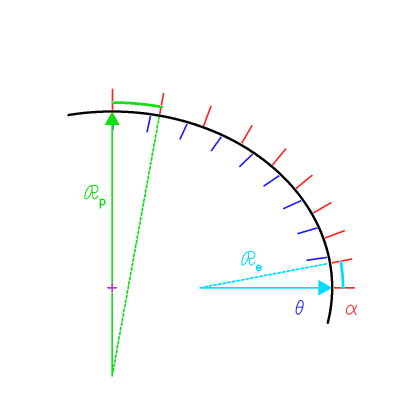
Rayons de courbure à l'équateur et au pôle
Crédit :
ASM

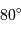 ) ainsi qu'au Pérou (vers
) ainsi qu'au Pérou (vers 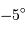 ). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
). Il s'agissait de lever une controverse concernant la "figure" de la Terre, c'est à dire sa forme : aplatie aux pôles, ou bien en forme de ballon de rugby ?
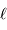 d'un arc de méridien d'ouverture
d'un arc de méridien d'ouverture 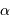 s'écrit en fonction du rayon de courbure
s'écrit en fonction du rayon de courbure 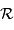 :
:
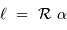
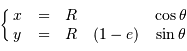
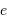 le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en
le paramètre marquant l'aplatissement.
Le rayon de courbure s'écrit, au 1er ordre en 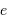 :
:
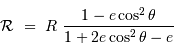
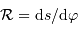 , avec
, avec 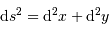 et
et 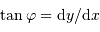 ].
].
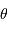 au pôle et à l'équateur, et y calculer
au pôle et à l'équateur, et y calculer 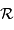 .
.


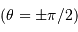 ou à l'équateur
ou à l'équateur 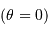 valent respectivement :
valent respectivement :
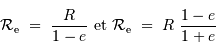
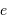 est petit, et les développements limités usuels, on trouve :
est petit, et les développements limités usuels, on trouve :
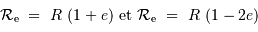
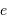 . En effet :
. En effet :