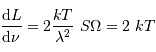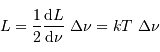Fond cosmologique
L'observation spectroscopique du rayonnement du fond cosmologique met en
évidence un rayonnement de corps noir, le corps noir cosmologique. Sa température
d'équilibre est de l'ordre de 3 K (2.728 K pour être très précis).
La loi de déplacement de Wien associe cette température à un maximum
d'émission dans les longueurs d'onde millimétrique.
Le corps noir cosmologique
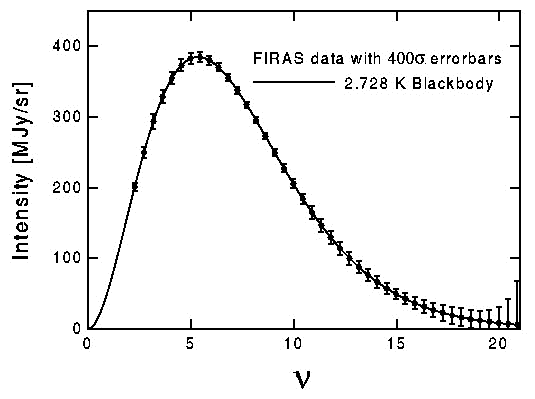
Le spectre du rayonnement du fond cosmologique est de type corps noir. Mesure de l'instrument FIRAS du satellite CoBE (Cosmic Background Explorer) de la NASA.
L'échelle spectrale est donnée en fréquence (unité =
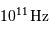
).
Crédit :
NASA
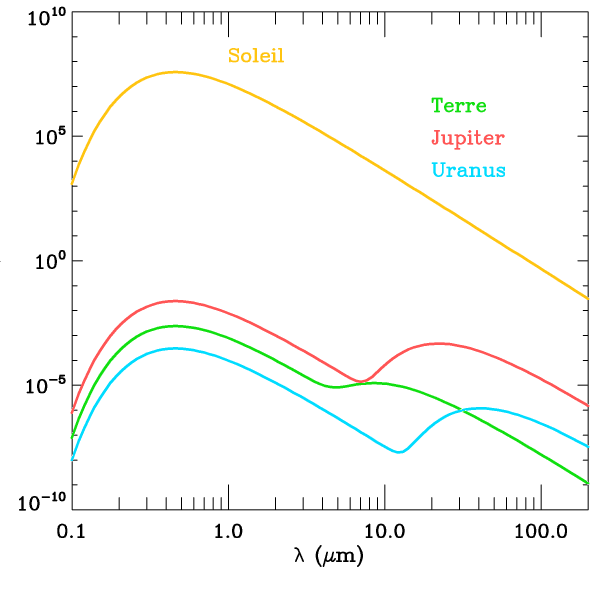
Spectre planétaire
L'allure d'un spectre
planétaire montre une courbe "à 2 bosses". Les 2 maximas locaux
piquent à 0.5 et 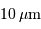 , soit à des températures effectives
de 6000 et 300 K approximativement.
, soit à des températures effectives
de 6000 et 300 K approximativement.
Les 2 contributions du spectre ont clairement 2 origines distinctes :
- La composante visible correspond à la réflexion du spectre
stellaire réfléchi par la planète
- La composante infrarouge rend compte du spectre de corps noir
planétaire. La planète est à l'équilibre thermique entre 2 sources :
l'apport énergétique de l'étoile (source chaude), et le rayonnement vers le ciel (source
froide).
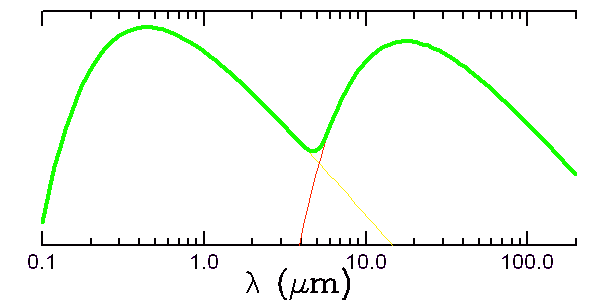
Spectre planétaire, à basse résolution
Deux composantes de type corps noir constituent le rayonnement des spectres planétaires à basse résolution spectrale : le spectre solaire réfléchi, et le spectre thermique.
Crédit :
ASM
Fond cosmologique
Dans le cadre de la théorie du big-bang, l'Univers est en expansion et se refroidit. Il est passé dans le passé par des phases plus chaudes, et a connu diverses étapes, correspondant à des ruptures d'équilibre.
Pour des température de plus 3000 K, la matière et le rayonnement était à l'équilibre, suite à l'interaction entre les électrons, libres, et les photons. Aux températures plus faibles, la recombinaison des électrons avec les protons pour former l'hydrogène atomique a occasionné le découplage de la matière et du rayonnement.
Ce dernier garde une distribution énergétique de corps noir, mais s'est refroidi suite à l'expansion de l'univers.
Il présente aujourd'hui une température, très homogène, de 2.728 K.
Spectres planétaires
En première approximation, on peut distinguer 2 composantes dans un spectre planétaire :
- Le spectre solaire directement réfléchi
- Le spectre infrarouge, rayonnée par la planète en fonction de sa température d'équilibre
Stricto sensu, le rayonnement n'est plus un rayonnement de corps noir. En fait, les 2 composantes sont proches de 2 corps noirs, l'un à la température du rayonnement stellaire, l'autre à la température d'équilibre planétaire.
Spectre planétaire, à basse résolution
Deux composantes de type corps noir constituent le rayonnement d'un spectre planétaire
observé à basse résolution spectrale.
Crédit :
ASM
 Température d'antenne
Température d'antenne
Difficulté : ☆☆☆
Temps : 45 min
Il a été vu que la luminance
spectrale du corps noir s'exprime,
en fonction de la fréquence
par :
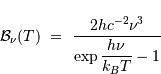
Dans cet exercice, on se propose de montrer comment cela conduit les
radio-astronomes à exprimer une luminosité radio comme une température, et donc
à l'exprimer en Kelvin.
Les conditions d'observation de l'image, définies par la
diffraction, énoncent
que le faisceau élémentaire observable a une étendue 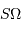 égale à
égale à 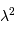 , et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur
, et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur 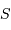 et sur
et sur 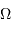 permet de passer de la luminance spectrale à la puissance spectrale.
permet de passer de la luminance spectrale à la puissance spectrale.
La surface 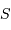 représente ici la
surface collectrice, et
représente ici la
surface collectrice, et 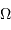 l'angle solide sous lequel est vue la
source élémentaire.
l'angle solide sous lequel est vue la
source élémentaire.
Question 1)
Montrer que, dans le domaine des radiofréquences, la fréquence
d'observation 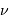 , typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
, typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
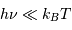
On donne 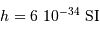 , et
, et 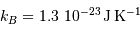 .
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
.
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
Ce n'est qu'une application numérique !
Question 2)
En déduire l'approximation de la loi de rayonnement dans le domaine
radio :
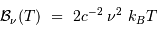
On rappelle le développement limité : 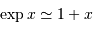 , pour
, pour 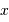 petit.
petit.
Question 3)
Montrer que l'intégration de la luminance spectrale 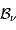 , vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
puissance égale à
, vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
puissance égale à
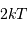
Faire le lien entre les termes de l'étendue de faisceau et les termes
énergétiques.
Question 4)
Déterminer alors la puissance reçue dans l'intervalle de fréquence
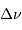 .
.
Il ne reste plus qu'à intégrer sur l'intervalle spectral, sans oublier
qu'une seule des deux polarisations est visible.
 Spectre d'une exoplanète
Spectre d'une exoplanète
Difficulté : ☆☆
Temps : 10 min
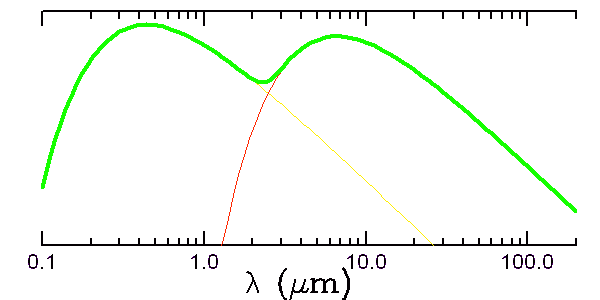
Spectre exoplanétaire simulé à basse résolution spectrale.
Crédit :
ASM
Question 1)
Interpréter la figure ci-jointe, simulant un spectre exoplanétaire.
[1 points]
Question 2)
Estimer les températures effectives associées à ce spectre.
[2 points]
Question 3)
Cette planète est supposée de type tellurique, de rayon égal à celui de
la Terre et située à 1 UA de son étoile, laquelle est de type à peu près
solaire. Comparer sa température d'équilibre à celle de la Terre.
Subit-elle un effet de serre important ?
[1 points]
- Question 1
Aide :
Ce n'est qu'une application numérique !
Solution :
L'énergie thermique est :
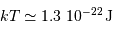
L'énergie d'un photon vaut 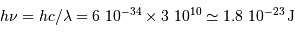 .
.
L'inégalité stricte demandée est bien vérifiée.
- Question 2
Aide :
On rappelle le développement limité : 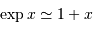 , pour
, pour 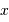 petit.
petit.
Solution :
Avec l'approximation 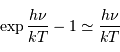 , valide vu l'hypothèse posée, on trouve :
, valide vu l'hypothèse posée, on trouve :
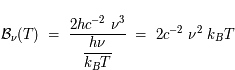
- Question 3
Aide :
Faire le lien entre les termes de l'étendue de faisceau et les termes
énergétiques.
Aide :
Intégrer simultanément la densité spectrale de luminance sur la surface collectrice
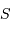 , et sur tout l'angle solide
, et sur tout l'angle solide 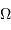 , avec la propriété admise :
, avec la propriété admise :
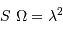 .
.
Solution :
La densité spectrale de luminance vaut :
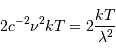
Intégrée sur la variable de surface 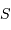 et celle d'angle solide
et celle d'angle solide 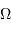 , on trouve, avec
, on trouve, avec 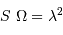 , une puissance monochromatique :
, une puissance monochromatique :
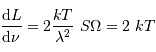
- Question 4
Aide :
Il ne reste plus qu'à intégrer sur l'intervalle spectral, sans oublier
qu'une seule des deux polarisations est visible.
Solution :
L'antenne n'est sensible qu'à une seule direction du champ électrique :
la moitié de l'énergie est donc perdue. En supposant la densité
spectrale de puissance uniforme sur l'intervalle de fréquence, on trouve
une puissance :
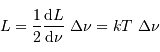
Cette valeur apparaît directement proportionnelle à la largeur de
l'intervalle spectral, fixée par la détection, et à la température de la
source.
C'est pourquoi les radioastronomes définissent la puissance
reçue par une température.
Cette température correspond directement à celle du corps s'il rayonne
comme un corps noir. Mais, toute énergie devenant ainsi une température
(température de bruit du
détecteur, ou de température d'antenne) par une simple règle de
proportionnalité, cette température ne peut pas être considérée, dans la
plupart des cas, comme une température thermodynamique.

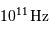 ).
).
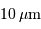 , soit à des températures effectives
de 6000 et 300 K approximativement.
, soit à des températures effectives
de 6000 et 300 K approximativement.


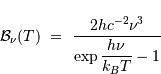
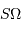 égale à
égale à 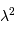 , et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur
, et que la mesure ne peut donner accès qu'à une
seule direction de polarisation. L'intégration sur 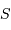 et sur
et sur 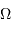 permet de passer de la luminance spectrale à la puissance spectrale.
permet de passer de la luminance spectrale à la puissance spectrale.
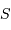 représente ici la
surface collectrice, et
représente ici la
surface collectrice, et 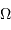 l'angle solide sous lequel est vue la
source élémentaire.
l'angle solide sous lequel est vue la
source élémentaire.
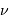 , typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
, typiquement de l'ordre du GHz, vérifie
pour les températures, même froides, rencontrées dans l'Univers :
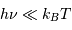
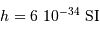 , et
, et 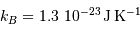 .
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
.
On considère comme
objet un nuage moléculaire à 10 K, et un rayonnement aux longueurs d'onde supérieures à 1 cm.
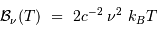
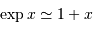 , pour
, pour 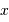 petit.
petit.
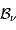 , vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
, vis à vis des variables angulaires et de surface, conduit à une densité spectrale de
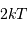
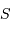 , et sur tout l'angle solide
, et sur tout l'angle solide 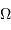 , avec la propriété admise :
, avec la propriété admise :
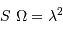 .
.
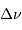 .
.

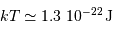
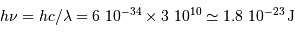 .
.
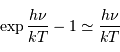 , valide vu l'hypothèse posée, on trouve :
, valide vu l'hypothèse posée, on trouve :
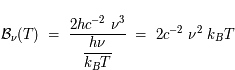
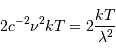
 et celle d'angle solide
et celle d'angle solide 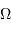 , on trouve, avec
, on trouve, avec 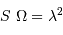 , une puissance monochromatique :
, une puissance monochromatique :