Applications liées au repère local-2
Auteur: Patrick Rocher
- Hauteur du plan équatorial au dessus de l'horizon
- Hauteur du plan équatorial au dessous de l'horizon
- Passage du Soleil au zénith entre les tropiques
- Exercice
- Trouver les limites des étoiles qui ne se lèvent pas
- Trouver les limites des étoiles qui ne se couchent pas
- Trouver les étoiles ayant une plus grande digression
- Distinction entre les étoiles circumpolaires et les étoiles ayant une plus grande digression
- Simulation
Hauteur du plan équatorial au dessus de l'horizon
Pour connaître l'angle entre le plan équatorial et le plan horizontal, on doit calculer l’intersection entre le plan équatorial et le méridien supérieur du lieu. Ce qui se traduit par une déclinaison nulle (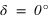 ) et le méridien supérieur => équation (1) ou (2) avec h positif.
) et le méridien supérieur => équation (1) ou (2) avec h positif.
La hauteur h obtenue avec l’équation (1) est positive (comprise entre 0° et 90°) si la latitude φ est comprise entre 0° et 90° donc dans l’hémisphère nord, la hauteur h de l’équateur sur l’horizon est égale à 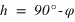 (colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
(colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
La hauteur h obtenue avec l’équation (2) est positive ou nulle (comprise entre 0° et 90°) si la latitude φ est comprise entre –90° et 0° donc dans l’hémisphère sud, la hauteur h de l’équateur sur l’horizon est égale à 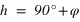 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie donc que la hauteur de l’équateur est bien le complémentaire de la latitude du lieu si le complémentaire est égal à 90° moins la valeur absolue de la latitude. De même la hauteur du pôle au-dessous de l’horizon, qui est le complémentaire de cet angle est égale à la valeur absolue de la latitude.
 Calcul de la hauteur de l'équateur
Calcul de la hauteur de l'équateur
Question 1)
Calculer la hauteur de l’équateur au méridien à Paris (latitude géographique : 48° 50' 11,2" N) et au Cap (latitude géographique : 33° 56' 0,0" S).
Hauteur du plan équatorial au dessous de l'horizon
Pour connaître l'angle entre l’équateur et le plan horizontal, on doit calculer l’intersection entre le plan équatorial et le méridien inférieur du lieu. Ce qui se traduit par une déclinaison nulle (φ = 0°) et le méridien inférieur => équation (3) ou (4) avec h négatif.
La hauteur h obtenue avec l’équation (3) est négative et comprise entre –90° et 0° si la latitude δ est comprise entre –90° et 0° donc dans l’hémisphère sud, la hauteur h de l’équateur sous l’horizon est égale à 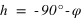 et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
La hauteur h obtenue avec l’équation (4) est négative et comprise entre -90° et 0° si la latitude δ est comprise entre 0° et 90° donc dans l’hémisphère nord, la hauteur h de l’équateur sous l’horizon est égale à 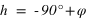 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
 Calcul de la hauteur du plan équatorial sous l'horizon
Calcul de la hauteur du plan équatorial sous l'horizon
Question 1)
Calculer la hauteur de l’équateur au dessous de l’horizon au méridien à Paris (latitude géographique : 48° 50' 11,2" N) et au Cap (latitude géographique : 33° 56' 0,0" S).
Passage du Soleil au zénith entre les tropiques
Exercice
 La déclinaison d'une étoile au zénith
La déclinaison d'une étoile au zénith
Question 1)
La direction du pôle Nord et l'équateur céleste nous fournissent des directions fixes pour toutes les sphères célestes liées aux observateurs individuels. Dans ce système de repérage, chaque étoile a sa propre déclinaison. Si, à un instant donné on voit une étoile au zénith d'un lieu particulier de latitude 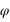 , quelle sera la déclinaison de cette étoile ?
, quelle sera la déclinaison de cette étoile ?
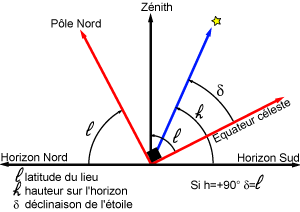
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
C'est la latitude du lieu ! Pourquoi ?
Trouver les limites des étoiles qui ne se lèvent pas
Pour un lieu quelconque de latitude φ, les étoiles qui ne se lèvent pas sont celles dont la hauteur du passage au méridien supérieur est toujours négative ou nulle.
- L’équation (1) donne
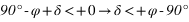
- L’équation (2) donne
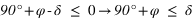
De plus la déclinaison doit toujours être comprise entre –90° et +90° donc la première inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 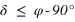 . De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant
. De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 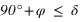 . Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
. Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
Auteur: P.Rocher
 Etoiles sous l'horizon
Etoiles sous l'horizon
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles qui ne se lèvent pas ?
Question 2)
Au Cap, en Afrique du sud (latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles qui ne se lèvent pas ?
Trouver les limites des étoiles qui ne se couchent pas
Pour qu'une étoile ne se couche pas, il faut que sa hauteur au passage au méridien inférieur soit positive ou nulle. On utilise donc les équations (3) et (4).
- L’équation (3) donne
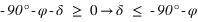
- L’équation (4) donne
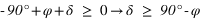
De nouveau, la déclinaison doit toujours être comprise entre –90° et +90° donc la première inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles circumpolaires doivent avoir une déclinaison vérifiant 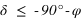 .
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant
.
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant 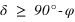 .
.
Cas particuliers : À l’équateur il n’y a aucune étoile circumpolaire. Au pôle Nord toutes les étoiles de déclinaisons positives sont circumpolaires et au pôle Sud toutes les étoiles de déclinaisons négatives sont circumpolaires.
Auteur: P. Rocher
 Exemples d'étoiles circumpolaires
Exemples d'étoiles circumpolaires
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles circumpolaires ?
Question 2)
Au Cap (Afrique du sud) (Latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles circumpolaires ?
Question 3)
Quelle est la latitude des lieux où le Soleil ne couche pas le jour du solstice d’été ? Quel est le nom de ce parallèle terrestre ? Montrer qu’en ces lieux le Soleil ne se lève pas le jour du solstice d’hiver.
Question 4)
Quels sont les lieux sur Terre où l’on voit, au cours de l’année, le plus d’étoiles ?
Question 5)
Quels sont les lieux sur Terre où l’on voit au cours de l’année le moins d’étoiles ?
Trouver les étoiles ayant une plus grande digression
On a vu que les étoiles qui ont une plus grande digression orientale ou occidentale sont les étoiles qui passent au méridien supérieur entre le zénith et le pôle.
Dans l’hémisphère nord : le passage au méridien supérieur doit se faire au nord (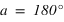 ) donc
) donc 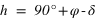 doit être inférieur à 90° donc
doit être inférieur à 90° donc 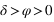 .
.
Dans l’hémisphère sud : le passage au méridien supérieur doit se faire au sud (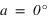 ) donc
) donc 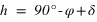 doit être inférieur à 90° donc
doit être inférieur à 90° donc 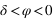 .
.
 Calcul des étoiles ayant une plus grande digression
Calcul des étoiles ayant une plus grande digression
Question 1)
À Paris (latitude géographique : 48° 50' 11,2" N) quelles sont les déclinaisons limites des étoiles qui ont une plus grande digression ?
Question 2)
Au Cap (Afrique du sud) (Latitude géographique : 33° 56' 0,0" S) quelles sont les déclinaisons limites des étoiles qui ont une plus grande digression ?
Distinction entre les étoiles circumpolaires et les étoiles ayant une plus grande digression
Il ne faut confondre étoiles circumpolaires et étoiles présentant une plus grande digression, c’est deux notions ne sont pas identiques. Par exemple dans l’hémisphère nord on a :
- Étoiles circumpolaires ⇔
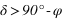 équation (1)
équation (1) - Plus grande digression ⇔
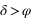 équation (2)
équation (2)
Si la latitude est supérieure à 45° la relation (2) implique (1), donc toutes les étoiles ayant une plus grande digression sont circumpolaires. Par contre, l’inverse n’est pas vrai (1) n’implique pas (2), donc toutes les circumpolaires n’ont pas forcément une plus grande digression. Par exemple pour une latitude de 50° nord, les étoiles ayant une déclinaison de 43° vérifient (1) (43°>40°), mais ne vérifient pas (2) (43°<50°).
Si la latitude est inférieure à 45°, c’est l’inverse : (1) implique (2), donc toutes les étoiles circumpolaires ont une plus grande digression, mais (2) n’implique pas (1) c’est-à-dire que toutes les étoiles ayant une plus grande digression ne sont pas forcément circumpolaires, par exemple pour une latitude de 30°, les étoiles ayant une déclinaison de 40° vérifient (2) (40°>30°), mais ne vérifient pas (1) (40°<60°).
Il y a identité entre les types d’étoiles que pour la latitude 45°.
Simulation
Pour bien comprendre les notions que nous venons de voir, on peut utliser la simulation suivante :
Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales 
Cette simulation affiche la sphère locale et la sphère équatoriale locale pour une latitude géographique φ et une longitude géographique L que l'on peut faire varier.
On peut choisir une position quelconque sur la sphère équatoriale (ascension droite α et déclinaison δ) et l'on peut faire évoluer la date et l'heure en temps universel (cela revient à faire tourner la Terre).
En bas de la simulation, on trouve les coordonnées calculées à partir des coordonnées équatoriales : angle horaire H, la hauteur h et l'azimut a.
Je vous propose de vérifier les points suivants :
- Placez-vous dans l'hémisphère nord en dehors de la bande intertropicale, à la longitude de Greenwich (L=0°,
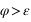 ) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.
) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h. - Placez-vous dans l'hémisphère sud en dehors de la bande intertropicale, à la longitude de Greenwich (L=0°,
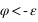 ), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.
), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h. - Pour une latitude nord proche de Paris (φ=49°), vérifier que les étoiles dont la déclinaison est supérieure à 90°-φ= 41° ne se couche pas. Vérifier que les étoiles dont la déclinaison est supérieure à 49° présentent une plus grande digression est et ouest et qu'elles passent au méridien supérieur (H=0°) et au méridien inférieur (H=12h) au nord (a=180°).Vérifier que les étoiles qui ont une déclinaison égale à la latitude du lieu passe au zénith du lieu.
- Faire la même chose avec un lieu de l'hémisphère sud.
Réponses aux exercices
pages_defrepere/mctc-exo-declinaison.html
Exercice
'La déclinaison d'une étoile au zénith'
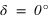 ) et le méridien supérieur => équation (1) ou (2) avec h positif.
) et le méridien supérieur => équation (1) ou (2) avec h positif.
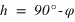 (colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
(colatitude du lieu) et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
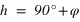 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
 Calcul de la hauteur de l'équateur
Calcul de la hauteur de l'équateur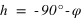 et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
et la direction de l’intersection de l’équateur avec le méridien est orientée au sud (a = 0°).
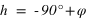 et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
et la direction de l’intersection de l’équateur avec le méridien est orientée au nord (a = 180°).
On vérifie bien que la hauteur de l’équateur sous l’horizon et l’opposée de la hauteur de l’équateur sur l’horizon.
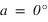 et
et 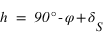 équation (1)
équation (1)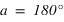 et
et 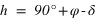 équation (2)
équation (2)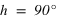 , alors a n’est plus défini, et :
, alors a n’est plus défini, et : 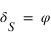
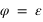 la solution est
la solution est 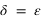 , donc le Soleil passe au zénith le jour du solstice d’été de juin. Un raisonnement identique pour le tropique du Capricorne montre que le Soleil passe au zénith uniquement le jour du solstice d’été de l’hémisphère sud. Sur l’équateur
, donc le Soleil passe au zénith le jour du solstice d’été de juin. Un raisonnement identique pour le tropique du Capricorne montre que le Soleil passe au zénith uniquement le jour du solstice d’été de l’hémisphère sud. Sur l’équateur 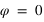 le Soleil passe au zénith deux fois par an lorsque sa déclinaison est nulle, c’est-à-dire aux équinoxes.
le Soleil passe au zénith deux fois par an lorsque sa déclinaison est nulle, c’est-à-dire aux équinoxes.
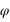 , quelle sera la déclinaison de cette étoile ?
, quelle sera la déclinaison de cette étoile ?

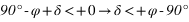
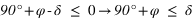
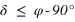 . De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant
. De même la seconde inéquation a des solutions que pour les latitudes négatives, donc dans l’hémisphère sud. On en conclut que dans l’hémisphère sud les étoiles qui ne se lèvent pas doivent avoir une déclinaison vérifiant 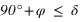 . Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
. Cas particulier à l’équateur aucune étoile ne se couche jamais, seules les étoiles qui ont une déclinaison de +/–90°, donc exactement aux pôles, sont en permanence sur l’horizon. Au pôle Nord on ne voit aucune des étoiles ayant une déclinaison négative et au pôle Sud on ne voit aucune des étoiles ayant une déclinaison positive. Ces remarques ne sont rigoureuses exactes qui si l’on néglige la réfraction atmosphérique.
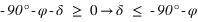
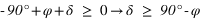
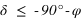 .
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant
.
De même la seconde inéquation a des solutions que pour les latitudes positives, donc dans l’hémisphère nord. On en conclut que dans l’hémisphère nord les étoiles circumpolaires doivent avoir une déclinaison vérifiant 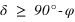 .
.
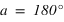 ) donc
) donc 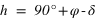 doit être inférieur à 90° donc
doit être inférieur à 90° donc 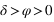 .
.
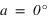 ) donc
) donc 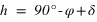 doit être inférieur à 90° donc
doit être inférieur à 90° donc 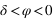 .
.
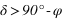 équation (1)
équation (1)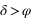 équation (2)
équation (2)
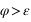 ) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.
) , prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire et l'azimut croissent avec le temps en faisant varier le temps de 0h à 23h.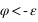 ), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.
), prennez un astre au-dessus de l'horizon et vérifier que l'angle horaire croît avec le temps alors que l'azimut décroît avec le temps, en faisant varier le temps de 0h à 23h.