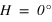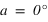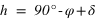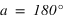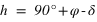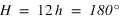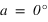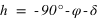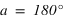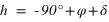Applications liées au repère local
Auteur: P. Rocher
- Introduction
- Quelques définitions supplémentaires
- Les astres circumpolaires
- Astres ayant une plus grande digression est et ouest
- Tracer de la sphère locale dans l'hémisphère sud
- Passage au méridien supérieur
- Exercice : Passage au méridien
- Passage d'un astre au méridien inférieur
- Conclusion
- QCM
Introduction
Tout ce que nous observons depuis la Terre se fait dans le repère local. Habitant dans l'hémisphère nord, nous sommes habitués à voir un ciel et des phénomènes liés à notre hémisphère. Nous allons dans les rubriques suivantes décrire des phénomènes pour un lieu quelconque de la Terre.
Quelques définitions supplémentaires
Un demi-cercle de la sphère céleste joignant le zénith au nadir porte le nom de demi-cercle d’égal azimut.
Le demi-cercle de la sphère céleste joignant le pôle céleste nord au pôle céleste sud et contenant le zénith porte le nom de méridien supérieur, par définition tous les points de ce demi-cercle ont un angle horaire nul (H = 0h = 0°), ce demi-cercle est toujours l’origine des angles horaires.
Le demi-cercle de la sphère céleste joignant le pôle céleste nord au pôle céleste sud et contenant le nadir porte le nom de méridien inférieur, par définition tous les points de ce demi-cercle ont un angle horaire de 12h (H = 12h = 180°).
Le demi-cercle d’égal azimut contenant le pôle céleste sud est souvent appelé méridien sud, c’est un abus de langage on devrait parler de demi-cercle d’azimut nul (a = 0°) ou d’azimut sud, ce demi-cercle est toujours l’origine des azimuts.
Le demi-cercle d’égal azimut contenant le pôle céleste nord est souvent appelé méridien nord, c’est également un abus de langage on devrait parler de demi-cercle d’azimut 180° (a = 180°) ou d’azimut nord.
Les astres circumpolaires
Suite à la rotation de la Terre autour de son axe, tous les astres passent au méridien inférieur et au méridien supérieur.
- Si les deux passages sont observables, l’astre est dit circumpolaire, il ne se couche pas.
- Si les deux passages sont inobservables, l’astre ne se lève pas.
- Si seul le passage supérieur est observable, l’astre se lève et se couche.
Par observable on entend que le passage serait visible en absence de Soleil c’est-à-dire qu’il n’aurait pas lieu sous l’horizon.
Astres circumpolaires
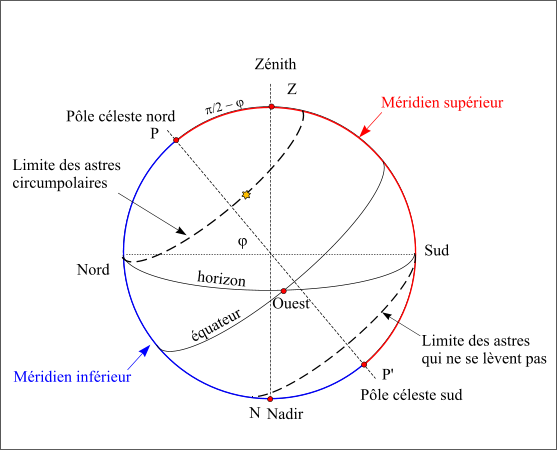
Figure 21 : Astres circumpolaires.
Crédit :
ASM/Patrick Rocher
Astres ayant une plus grande digression est et ouest
Par contre, tous les astres ne passent pas tous au méridien nord et au méridien sud, en effet certains astres passent deux fois dans le méridien nord (a = 180°) ou deux fois dans le méridien sud (a = 0°). Pour un lieu de l’hémisphère nord, ce sont les astres qui passent entre le zénith et le pôle céleste nord (observable) ou entre le nadir et le pôle céleste sud (inobservable, car toujours sous l’horizon). Comme l’azimut ne varie plus de 0° à 360°, il présente deux valeurs extrêmes (une entre 0° et 180° et l’autre entre 180° et 360°). C’est deux valeurs extrêmes correspondent aux plus grandes digressions ouest et est de l’astre.
Plus grande digression d'un astre.
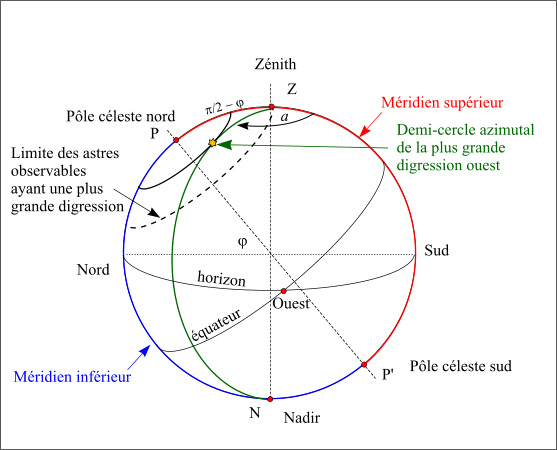
Figure 22 : Plus grande digression d'un astre.
Crédit :
ASM/Patrick Rocher
Tracer de la sphère locale dans l'hémisphère sud
On voit très souvent une représentation de la sphère céleste locale pour un lieu de l’hémisphère nord, il est intéressant de tracer également la sphère céleste locale pour un lieu de l’hémisphère sud.
Sphère locale dans l'hémisphère nord
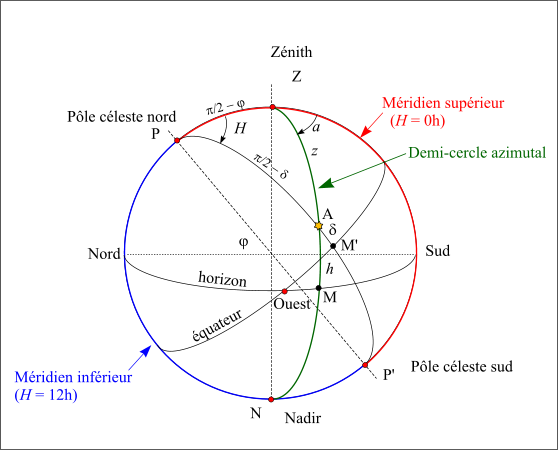
La sphère locale dans l'hémisphère nord.
Crédit :
ASM/Patrick Rocher
La sphère locale dans l'hémisphère sud
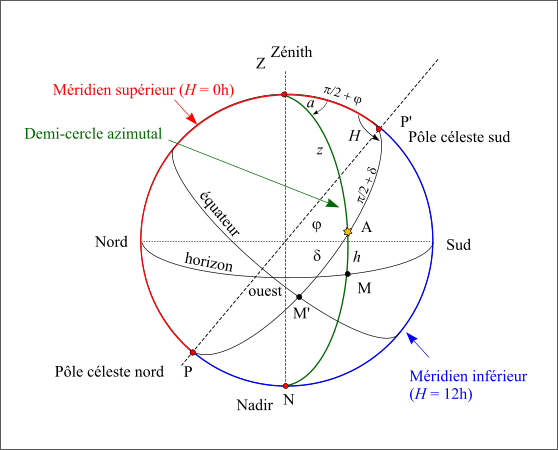
La sphère locale dans l'hémisphère sud.
Crédit :
ASM/Patrick Rocher
On remarque bien que l’angle horaire H d’un astre est croissant avec le temps que l’on soit dans l’hémisphère nord ou dans l’hémisphère sud, par contre l’azimut de l’astre (a) décroit avec le temps dans l’hémisphère sud alors qu’il croît avec le temps dans l’hémisphère nord. Ce choix de variables croissantes avec le temps est volontaire, il s'oppose à la logique mathématique qui favorise des repères directs.
Passage au méridien supérieur
Il y a deux méthodes pour étudier les conditions d’un passage au méridien supérieur, soit faire des dessins de chaque cas de figure en fonction de la latitude du lieu et déterminer les résultats par des raisonnements purement géométriques, soit utiliser une méthode analytique en regardant les résultats sur l’azimut obtenus en fixant la valeur de l’angle horaire lorsque l’astre est dans le méridien. C'est cette seconde méthode que nous allons utiliser.
Les équations ci-dessous montrent qu'on a alors deux solutions :
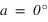 et
et 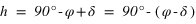 équation (1)
équation (1)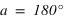 et
et 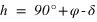 équation (2)
équation (2)
Avec la condition supplémentaire liée à la définition de la hauteur : 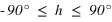 .
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si
.
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si 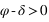 donc si
donc si 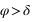 . Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si
. Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si 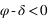 donc si
donc si 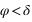 . Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors
. Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors 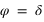 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.
Passage au méridien supérieur.
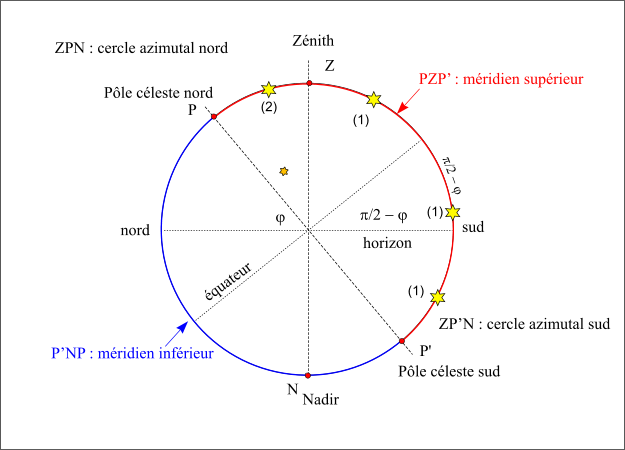
Figure 24 : Passage au méridien supérieur.
Crédit :
ASM/Patrick Rocher
Sur la figure, on a fait une coupe méridienne de la sphère céleste. Le méridien supérieur est représenté en rouge c’est le demi-cercle PZP’. L’étoile notée (2) passe au méridien supérieur avec un azimut nord (elle est sur l’arc ZPN), sa hauteur est comptée à partir de la direction nord de l’horizon.
Les autres étoiles, notées (1), passent au méridien supérieur avec un azimut sud (elles sont sur l’arc ZP’N) leurs hauteurs sont comptées à partir de la direction sud de l’horizon ; deux passent au-dessus de l’horizon, la troisième passe sous l’horizon, car une partie du méridien supérieur est sous l’horizon (sud-P’).
On remarquera aussi que la médiation de l’astre correspond à la longitude de l’écliptique qui passe au méridien en même temps que l’astre.
Exercice : Passage au méridien
Auteur: P. Rocher
 Passage du Soleil au méridien
Passage du Soleil au méridien
Difficulté : ☆☆☆
La déclinaison du Soleil varie au cours de l’année de –23° 26' 21" (au solstice d’hiver) à 23° 26' 21" (au solstice d’été) en passant par 0° (aux équinoxes).
Question 1)
Quelles sont les hauteurs du Soleil à son passage au méridien supérieur à Paris (latitude géographique : 48° 50' 11,2" N) au début de chaque saison astronomique.
On utilisera les deux solutions (1) et (2) avec la condition portant sur la hauteur, pour choisir la bonne solution.
Question 2)
Quelles sont les hauteurs du Soleil à son passage au méridien supérieur au Cap (latitude géographique : 33° 56' 0,0" S) au début de chaque saison.
Question 3)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour du solstice d’été ? Quel est le nom de ce parallèle terrestre ?
Question 4)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour du solstice d’hiver ? Quel est le nom de ce parallèle terrestre ?
Question 5)
Quelle est la latitude des lieux où le Soleil passe au zénith le jour des équinoxes ? Quel est le nom de ce parallèle terrestre ?
Passage d'un astre au méridien inférieur
Par définition, à l'instant du passage au méridien inférieur, l'angle horaire est égale à 180° (H = 180°).
Les équations ci-dessous montrent qu'on a donc deux solutions :
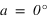 et
et 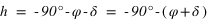 équation (3)
équation (3)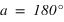 et
et 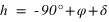 équation (4)
équation (4)
Avec toujours la condition supplémentaire : 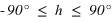 . On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si
. On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si 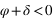 donc si
donc si 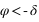 . Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si
. Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si 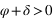 donc si
donc si 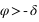 . Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors
. Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors 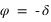 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.
Passage au méridien inférieur
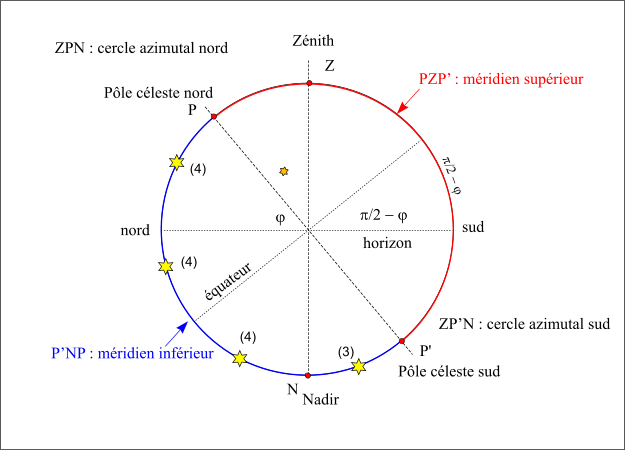
Figure 25 : Passage au méridien inférieur.
Crédit :
ASM/Patrick Rocher
Sur la figure, on a fait une coupe méridienne de la sphère céleste. Le méridien inférieur est représenté en bleu c’est le demi-cercle PNP’. L’étoile notée (3) passe au méridien inférieur avec un azimut nord (elle est sur l’arc ZP’N), sa hauteur est comptée à partir de la direction sud de l’horizon.
Les autres étoiles, notées (4), passent au méridien inférieur avec un azimut nord (elles sont sur l’arc ZPN) leurs hauteurs sont comptées à partir de la direction nord de l’horizon ; une passe au dessus de l’horizon, car une partie du méridien inférieur est au-dessus de l’horizon (nord -P), les deux autres passent sous l’horizon.
Conclusion
QCM
Réponses aux QCM
pages_applications/mctc-qcm-reperage.html
QCM
'QCM sur le repérage d'un astre'
- Question 1
Solution : réponse 2)
(
Les deux dernières réponses sont bonnes
)
Solution : réponse 3)
(
Les deux dernières réponses sont bonnes
)
- Question 2
Solution : réponse 1)
(
oui, l'angle horaire se compte à partir de la direction du Sud dans le repère équatorial local
)
- Question 3
Solution : réponse 3)
(
oui, c'est le moyen de trouver l'origine des ascensions droites dans le ciel : le temps sidéral n'est pas un temps mais un angle.
)
- Question 4
Solution : réponse 2)
- Question 5
Solution : réponse 2)
(
oui pour les astronomes (mais les géomètres mesurent les azimuts à partir du Nord)
)
- Question 6
Solution : réponse 1)
(
Avec un instrument méridien, l'angle horaire est nul: Le temps sidéral local est égal à l'ascension droite au moment du passage au méridien.
)
Solution : réponse 2)
(
Avec un instrument méridien, l'angle horaire est nul. L'instrument méridien observe exclusivement vers le Sud
)
Réponses aux exercices
pages_defrepere/exercice-meridien.html
Exercice
'Passage du Soleil au méridien'




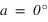 et
et 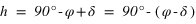 équation (1)
équation (1)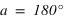 et
et 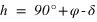 équation (2)
équation (2)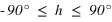 .
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si
.
On remarque qu’il y a toujours une seule solution qui réponde à ce système, en effet :
La hauteur issue de l’équation (1) est inférieure à 90° si 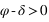 donc si
donc si 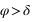 . Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si
. Dans ce cas le passage au méridien supérieur se fait au sud (a = 0°).
La hauteur issue de l’équation (2) est inférieure à 90° si 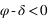 donc si
donc si 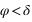 . Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors
. Dans ce cas le passage au méridien supérieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de 90°, donc si le corps passe au zénith, alors 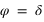 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.

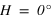 ) les équations de transformations de coordonnées donnent :
) les équations de transformations de coordonnées donnent :
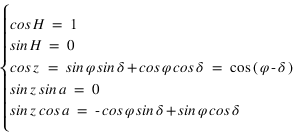
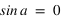 alors
alors 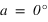 ou
ou 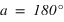 , si
, si 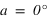 alors
alors 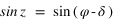 et si
et si 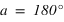 alors
alors 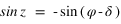 .
.
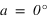 et
et 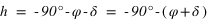 équation (3)
équation (3)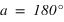 et
et 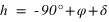 équation (4)
équation (4)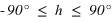 . On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si
. On remarque qu’il y a toujours une seule solution qui réponde à ce système.
La hauteur issue de l’équation (3) est supérieure à –90° si 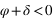 donc si
donc si 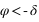 . Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si
. Dans ce cas le passage au méridien inférieur se fait au sud (a = 0°).
La hauteur issue de l’équation (4) est supérieure à –90° si 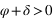 donc si
donc si 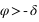 . Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors
. Dans ce cas le passage au méridien inférieur se fait au nord (a = 180°).
Cas particulier, si la hauteur est de –90°, donc si le corps passe au nadir, alors 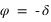 . Dans ce cas l’azimut n’est pas défini.
. Dans ce cas l’azimut n’est pas défini.

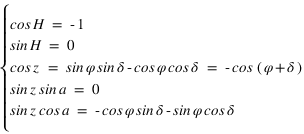
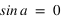 alors
alors 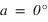 ou
ou 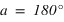 . Si
. Si 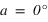 alors
alors 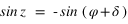 et si
et si 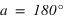 alors
alors 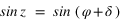 .
.