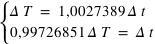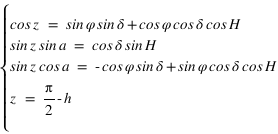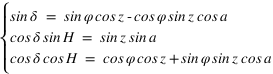Les repères locaux
Auteur: Patrick Rocher
- Introduction
- Le système de coordonnées équatoriales horaires
- Exercice
- Effet d'un changement de longitude terrestre
- La variation du temps sidéral
- Le repère local
- Quelques définitions supplémentaires
- Formulaires liant les coordonnées locales
- Remarque sur le repère local (alt-azimutal)
- Simulations
- Exercices d'utilisation des simulations
Introduction
Les deux repères écliptique et équatorial sont fixes pour une époque donnée, même centrés au centre de la Terre, ils ne tiennent pas compte du mouvement de l’observateur, ni de sa position. Nous allons décrire deux nouveaux repères qui vont être liés à un observateur sur la Terre. Ces repère vont donc tourner avec notre planète. Nous devons donc, dans un premier temps, exprimer la rotation de la Terre par rapport au répère équatorial terrestre.
Le système de coordonnées équatoriales horaires
Le temps sidéral
Ce système est un système intermédiaire dans lequel le repère équatorial est lié à la Terre, c’est-à-dire qu’il tourne avec elle. Il est caractérisé par un méridien origine (le méridien du lieu) et un angle qui donne la position du point vernal (direction de l’équinoxe de printemps) par rapport à ce méridien. Cet angle s’appelle le temps sidéral local (noté TL). Cet angle est exprimé en heures sexagésimales, il est compté positivement vers l’ouest (sens des aiguilles d’une montre) à partir du méridien local. Ainsi l’angle temps sidéral local croît avec le temps.
Le temps sidéral local à Greenwich
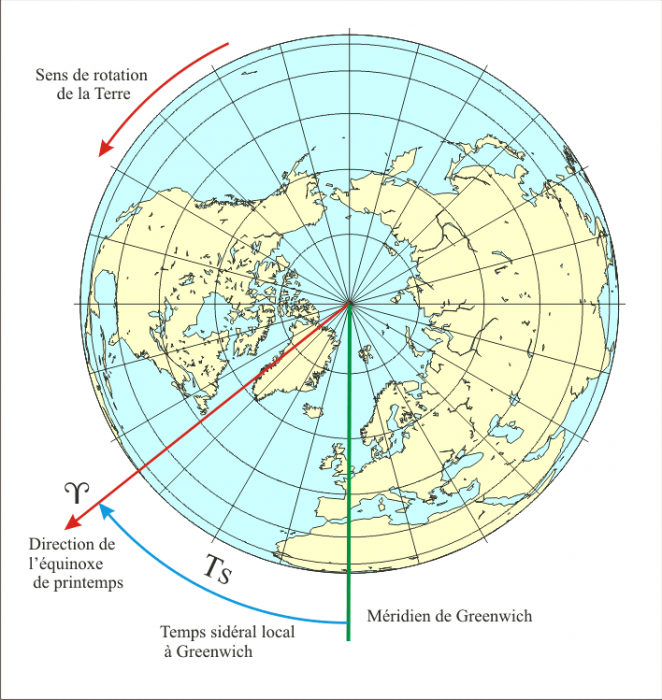
Figure 17 : Le temps sidéral local.
Crédit :
ASM/Patrick Rocher
Les coordonnées équatoriales horaires
Le système de coordonnées équatoriales horaires est un système polaire dont le plan de base (Oxy) est l’équateur céleste, Ox est la direction du méridien local, Oy est dans le sens indirect (90° vers l’ouest) et Oz est l’axe du pôle céleste. Le premier angle est l’angle horaire (noté H), compté positivement en heures sexagésimales de 0h à 24h vers l’ouest à partir du méridien du lieu, le second angle est la déclinaison (le même angle que celui du repère équatorial). L’angle horaire, comme le temps sidéral, croît avec le temps.
Les petits cercles parallèles à l’équateur portent le nom de parallèles célestes et les demi-grands cercles joignant les pôles célestes portent le nom de cercles horaires. Tous les astres qui ont une déclinaison constante décrivent dans le mouvement diurne un parallèle céleste. En particulier, l'étoile Polaire décrit actuellement un petit cercle dont le rayon est inférieur à 1° autour du pôle céleste, ce qui nous permet de situer le pôle céleste à un degré près. Cela n’a pas toujours été le cas. Ainsi au XIIIe siècle d’étoile polaire était à 4° du pôle céleste cela en raison de la précession des équinoxes.
Repère équatorial horaire
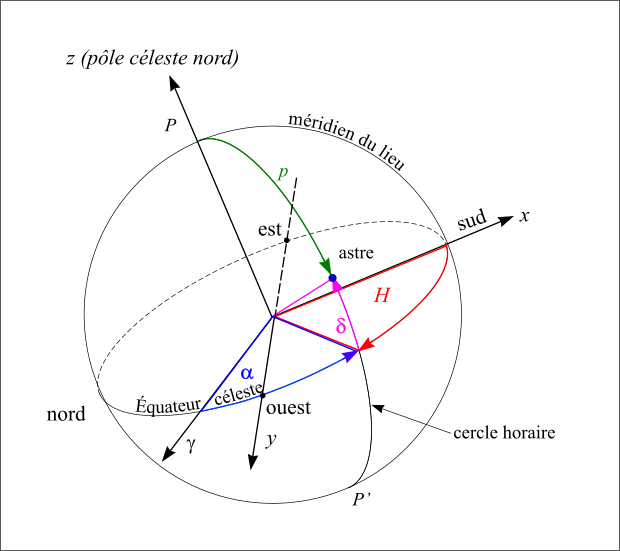
Figure 18 : Repère équatorial local.
Crédit :
ASM/Patrick Rocher
On a une relation simple entre l’ascension droite, l’angle horaire et le temps sidéral local :
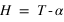
Attention dans les formules ces angles doivent être dans le même système d’unités.
On remarquera que l’angle horaire d’un astre est le même pour tous les lieux situés sur un même méridien terrestre.
Compte tenu de la définition de l’angle horaire, le temps sidéral local est l’angle horaire du point vernal.
Exercice
 Le temps sidéral
Le temps sidéral
Question 1)
Quelle est l'ascension droite α d'une étoile passant au méridien d'un lieu donné à un instant donné ?
Quelle est la valeur de l'angle horaire d'un astre qui passe au méridien? Quelle est la formule fondamentale liant l'ascension droite et l'angle horaire?
Effet d'un changement de longitude terrestre
Si l’on change de méridien, à un instant donné, le temps sidéral local du nouveau méridien est égal au temps sidéral de l’ancien méridien augmenté de la différence de longitude si le nouveau méridien est à l’est de l’ancien ou diminué de la différence de longitude si le nouveau méridien est à l’ouest de l’ancien. Attention les longitudes doivent être dans le même système d’unités que le temps sidéral (généralement en heures sexagésimales). Attention également aux conventions pour la notation des longitudes : dans le passé les longitudes étaient comptées négativement vers l’est (de 0° à -180° ou 0h à -12h) et positivement vers l’ouest (de 0° à 180° ou 0h 12h) à partir du méridien de Greenwich. La formule donnant le temps sidéral local TL en un lieu de longitude L par rapport au temps sidéral à Greenwich TG était donc :
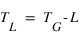
De nos jours les conventions sur la longitude ont changé, la longitude est comptée positivement vers l’est à partir du méridien de Greenwich de 0° à 360° (ou de 0h à 24h) la formule précédente se transforme donc en :
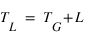
On trouve donc les deux formules dans la littérature et cela est la source de nombreuses erreurs de calcul. Pour les éviter, il suffit de se souvenir que le temps sidéral croît par rapport à Greenwich lorsque la longitude est vers l’est et décroit lorsque la longitude est vers l’ouest. N’oubliez pas non plus que certaines cartes donnent la longitude par rapport au méridien de Paris en grade !
La variation du temps sidéral
Le temps sidéral est l’angle horaire de la direction de l’équinoxe de printemps (le point gamma), il varie (en moyenne) de 24h (ou 360°) en 23h 56min 4s de temps moyen.
Cela permet de calculer le temps sidéral local en tout point de la Terre à un instant t à partir de la connaissance du temps sidéral au méridien de Greenwich à 0h. Le calcul se fait en deux étapes : on calcule le temps sidéral à Greenwich à l’instant t, puis le temps sidéral au lieu considéré en ajoutant ou en retranchant la longitude du lieu.
Relations entre la variation du temps moyen 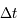 et la variation
et la variation 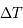 du temps sidéral :
du temps sidéral :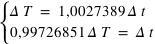
Nous sommes capables de construire une horloge de temps sidéral local. Sur ces horloges, l’aiguille des heures fait deux tours en 23h 56min 4s de notre échelle de temps. La connaissance du temps sidéral est importante, car elle permet de calculer l’angle horaire d’un astre (angle qu’il fait avec la direction du sud, lorsque l’on connaît son ascension droite. Inversement lorsque l’on connait le temps sidéral local d’un événement on peut en déduire :
- le temps moyen de l’événement si on connaît la longitude du lieu,
- la longitude du lieu si l’on connaît le temps moyen de l’événement.
Remarque : Comme ce repère local ne dépend que de la longitude, on peut le placer au centre de la Terre ou sur un lieu quelconque situé sur le méridien. Nous verrons que ce changement d’origine modifie la valeur des coordonnées pour des astres proches (parallaxe diurne).
Auteur: P. Rocher
 Calcul du temps sidéral local en un lieu donné
Calcul du temps sidéral local en un lieu donné
Difficulté : ☆☆☆
Question 1)
Déterminer le temps sidéral local à Paris le 30 mars 2010 à 18h 3m 42s UTC (l’heure UTC est le temps moyen de Greenwich) à Paris (longitude : 9min 21s est). Le temps sidéral à Greenwich à 0hUTC étant de 12h 29min 7s.
Faire une règle de trois en sachant qu'en 23h 56min 4s de temps moyen le temps sidéral varie de 24h ou utiliser directement les formules de conversions.
Le repère local
En un lieu donné, de latitude géographique φ et de longitude géographique L on peut définir un repère local dont le plan Oxy est par le plan horizontal tangent à l’ellipsoïde au lieu considéré et dont l’axe Oz est la normale à ce plan (direction du zénith). Comme dans le cas des coordonnées horaires, l’axe Ox est l’intersection du plan du méridien et du plan horizontal (direction du sud) et l’axe Oy est à 90° compté vers l’ouest dans le sens indirect (direction de l’ouest). On appelle premier vertical ouest le demi-plan vertical passant par la verticale du lieu et la direction de l’ouest. On définit de même le premier vertical est comme le demi-plan vertical passant par la direction de l’est.
Le premier angle est compté positivement à partir du sud vers l’ouest (sens indirect – sens des aiguilles d’une montre) de 0° à 360° et s’appelle l’azimut des astronomes (noté a). On a donc les relations suivantes :
sud ⇔ azimut = 0°, ouest ⇔ azimut = 90°, nord ⇔ azimut = 180° et est ⇔ azimut = 270°. La direction de la vertical, vers le haut, d'un lieu porte le nom de zénith, sa direction opposée, vers le bas, porte le nom de nadir.
Le second angle est compté positivement vers le zénith de 0° à 90°et négativement vers le nadir de 0° à –90°, il porte le nom de hauteur (noté h). À la place de la hauteur, on utilise parfois l’angle entre la direction du zénith et la direction de l’astre, cet angle est compté de 0° à 180° à partir du zénith et porte de nom de distance zénithale (notée z).
Repère local azimutal
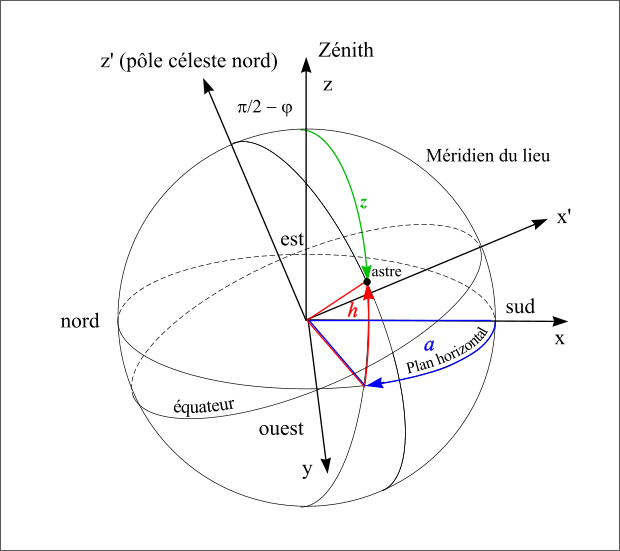
Figure 19 : Repère local azimutal.
Crédit :
ASM/Patrick Rocher
Quelques définitions supplémentaires
Lors du lever d’un astre, sa hauteur apparente est nulle (h = 0), on donne parfois l’angle entre la direction de l’est et la direction de l’astre à son lever, cet angle porte le nom d’amplitude ortive. De même lors du coucher d’un astre, on donne parfois l’angle entre la direction de l’ouest et la direction de l’astre à son coucher, cet angle porte le nom d’amplitude occase.
Enfin les cercles de hauteurs égales, petits cercles de la sphère céleste parallèles à l’horizon, portent le nom almicantarat.
Pour un lieu de l’hémisphère nord, l’angle entre le zénith et le pôle céleste nord est égal au complémentaire de la latitude du lieu (π/2 – φ). Le complémentaire de la latitude porte le nom de colatitude.
C’est aussi l’angle entre le plan équatorial céleste et le plan horizontal.
Formulaires liant les coordonnées locales
Le triangle sphérique construit avec le pôle céleste nord, le zénith du lieu et la direction d’un astre est le suivant :
triangle-local
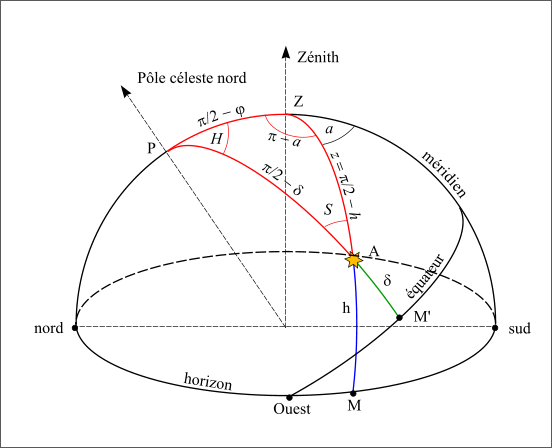
Figure 20 : Triangle sphèrique local.
Crédit :
ASM/Patrick Rocher
En utilisant les relations de trigonométrie sphérique sur les cinq angles connus, on démontre les relations suivantes :
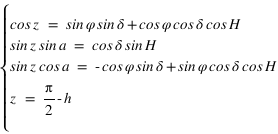
et inversement
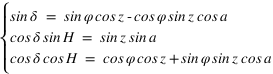
Le sixième angle, formé par les directions du zénith et du pôle céleste vues depuis l’astre porte le nom d’angle à l’astre (noté S).
Remarque sur le repère local (alt-azimutal)
Les géographes et les marins utilisent un azimut compté également dans le sens indirect, mais à partir du nord. L’azimut d’un astre pour un lieu de l’hémisphère nord croît avec le temps ainsi le Soleil se déplace d’est en ouest en passant vers le sud.
Inversement dans l’hémisphère sud l’azimut décroit avec le temps, ainsi le Soleil se déplace d’est en ouest en passant vers le nord.
Les montres ayant été inventées dans l’hémisphère nord, les aiguilles de la montre suivent le mouvement de l’ombre des cadrans solaires de l’hémisphère nord donc est-sud-ouest.
Dans l’hémisphère nord la hauteur du pôle céleste est égale à la latitude du lieu (en fait ce n’est pas tout à fait vrai en raison de la réfraction atmosphérique).
Simulations
Pour bien comprendre les systèmes de coordonnées, on peut utiliser les simulations suivantes.
 Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales
Coordonnées équatoriales et horizontales 
La première simulation affiche la position d'un astre sur la sphère céleste, en coordonnées équatoriales (α, δ) et en coordonnées horizontales (a, h). On y voit aussi le point vernal γ et l'angle horaire H. Z est le zénith et P est le pôle céleste.
Les paramètres de la simulation sont les suivants :
- Coordonnées équatoriales de l'astre, ascension droite α et déclinaison δ ;
- position sur Terre, latitude φ et longitude L ;
- date et heure en temps universel.
En bas de la simulation, on trouve les données calculées à partir des paramètres : angle horaire H, hauteur h et azimut a.
On peut trouver les coordonnées et le fuseau horaire d'une ville sur le web.
 Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique
Position du Soleil sur l'écliptique 
La deuxième simulation montre la position du Soleil sur l'écliptique à une date donnée. Cette simulation montre l'inclinaison de l'écliptique par rapport à l'équateur ε, la longitude écliptique λ, l'ascension droite α et la déclinaison δ. P est le pôle Nord céleste et K est le pôle Nord de l'écliptique. Les quantités calculées par rapport à la date et affichées en bas sont λ, α et δ.
Les coordonnées équatoriales du Soleil variant peu au court d'une journée, on peut les obtenir à partir de cette simulation pour une date donnée, et les utiliser dans la première simulation pour voir la position du Soleil en coordonnées horizontales pendant la journée.
Exercices d'utilisation des simulations
Auteur: Damien Guillaume
 Visibilité des étoiles
Visibilité des étoiles
Difficulté : ☆☆
Cet exercice propose d'utiliser l'applet Coordonnées équatoriales et horizontales pour déterminer la visibilité d'étoiles en différents endroits sur Terre.
Données
- Sirius : ascension droite α = 6h 45m, déclinaison δ = -16° 43'
- Dubhe : α = 11h 04m, δ = +61° 45'
- France (Paris) : latitude φ = +49°, longitude L = 2° E, fuseau horaire = UTC+1
- Afrique du Sud (Cape Town) : φ = -34°, L = 18° E, UTC+2
- Japon (Tokyo) : φ = 36° N, L = 140° E, UTC+9
Question 1)
A l'aide de l'applet, trouver les mois de l'année où Sirius est visible à minuit en France (à Paris), en Afrique du Sud (Cape Town) et au Japon (Tokyo).
Attention au décalage horaire !
Pour simplifier, on pourra prendre minuit heure locale sans tenir compte des différences heures d'été / heures d'hiver.
Par convention, la longitude est positive vers l'Est. Donc 140° E = +140°.
Question 2)
Même question pour l'étoile Dubhe (α UMa).
Question 3)
Expliquer les résultats.
Réponses aux QCM
pages_repere-locaux/utilisation-simulations.html
QCM
'Systèmes de coordonnées'
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 1)
- Question 3
Solution : réponse 2)
- Question 4
Solution : réponse 2)
- Question 5
Aide :
Commencer par chercher la valeur de la déclinaison pour laquelle la hauteur est maximum à l'aide de la première simulation, en prenant en compte la réponse à la question précédente. Vérifier qu'un changement d'ascension droite ne modifie pas le résultat.
Aide :
A partir de la déclinaison, on peut obtenir l'ascension droite correspondante à l'aide de la deuxième simulation.
Solution : réponse 1)
- Question 6
Solution : réponse 2)
- Question 7
Solution : réponse 3)
- Question 8
Solution : réponse 3)
Réponses aux exercices
pages_defrepere/mctc-exo-temps-sideral.html
Exercice
'Le temps sidéral'
pages_defrepere/variation-temps-sideral.html
Exercice
'Calcul du temps sidéral local en un lieu donné'
pages_defrepere/utilisation-simulations.html
Exercice
'Visibilité des étoiles'
- Question 1
Aide :
Attention au décalage horaire !
Pour simplifier, on pourra prendre minuit heure locale sans tenir compte des différences heures d'été / heures d'hiver.
Aide :
Par convention, la longitude est positive vers l'Est. Donc 140° E = +140°.
- Question 2
- Question 3

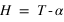

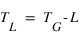
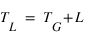
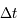 et la variation
et la variation 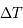 du temps sidéral :
du temps sidéral :