Intérêt d'un collecteur de grand diamètre
Deux motifs se conjuguent pour privilégier les collecteurs de grand diamètre : la taille de la tache de diffraction et le flux collecté. Comme le montre la table ci-joint, le flux reçu par unité d'élément d'image résolvant varie comme la puissance quatrième du diamètre collecteur, lorsque la taille de la tache image est limitée par la diffraction et que le détecteur échantillonne cette tache image. Le gain obtenu provient d'une part de l'accroissement de la surface collectrice, d'autre part d'une meilleure finesse de la tache de diffraction.
| diamètre collecteur | flux total | surface tache image | flux/pixel |
| 1 | 1 | 1 | 1 |
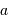 | 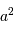 | 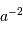 | 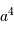 |
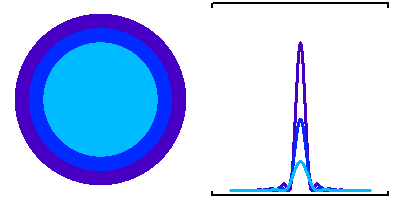
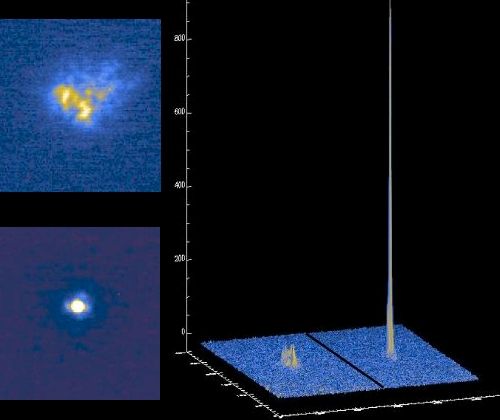
De l'intérêt d'arriver à la tache de diffraction
Il est utile de s'attacher à récupérer une forte densité de flux sur les pixels, comme le montre cet exemple de traitement par optique adaptative.

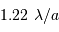 .
L'abscisse du profil en coupe est directement donnée en unité
.
L'abscisse du profil en coupe est directement donnée en unité 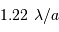 .
.
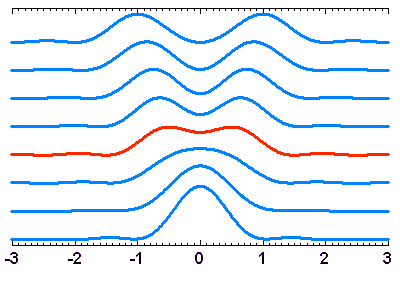
Le critère de Rayleigh
Les schémas ci-joints illustrent le critère de Rayleigh, qui définit la condition pour distinguer 2 objets de magnitude identique angulairement voisins.
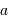
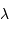
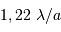

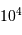
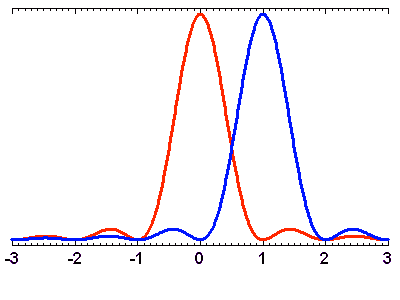
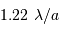
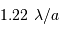
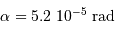 , soit environ 11".
, soit environ 11".
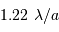 ; soit le diamètre :
; soit le diamètre :