 Introduction
Introduction
Cette dernière section est purement mathématiques, elle présente un des calculs effectués par Aristarque de Samos dans son traité sur la grandeur et la distance du Soleil et de la Lune. Puis nous étudions les deux observations effectuées par Ptolémée et décrites dans l'Almageste, ces observations permettent de calculer le diamètre apparent de la Lune, puis les distances Terre-Lune et Terre-Soleil. On compare à cette occasion les valeurs calculées par Ptolémée avec les valeurs actuelles.
Aristarque de Samos (310 - 230 av. J.-C.) fut l'élève de Straton de Lampsaque, il est l'auteur du premier système héliocentrique, système décrit dans son livre "Les Hypothèses" (disparu) cité par Archimède dans son traité de l'Arénaire. Aristarque est également l'auteur du traité sur la grandeur et la distance du Soleil et de la Lune.
Pour le calcul des distances Terre-Lune et Terre-Soleil, il fait les hypothèses suivantes :
- 1. La Lune reçoit la lumière du Soleil.
- 2. La Terre peut être considérée comme un point et comme le centre de l'orbite de la Lune.
- 3. Lorsque la Lune nous parait dikhotome (coupée en deux portions égales), elle offre à nos regards son grand cercle, qui détermine la partie éclairée et la partie obscure de cet astre.
- 4. Lorsque la Lune nous parait dikhotome, sa distance du Soleil est moindre du quart de la circonférence, de la trentième partie de ce quart.
- 5. La largeur de l'ombre est de deux Lunes.
- 6. L'arc soutendu dans le ciel par la Lune est la quinzième partie d'un signe.
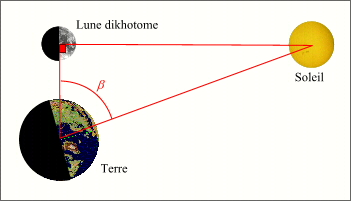
L'hypothèse 4 d'Aristarque
Crédit : IMCCE/Patrick Rocher
Comme on le constate certaines de ces hypothèses sont fausses, l'hypothèse 4 revient à donner à l'angle β la valeur de 87°. Cette erreur explique son l'erreur sur le calcul de la distance Terre-Soleil. L'hypothèse 6 donne à la Lune un diamètre de 2°, valeur quatre fois trop forte.
À partir de ces hypothèses, Aristarque va déduire que la distance Soleil-Terre est supérieure à 18 fois la distance Terre-Lune et inférieure à 20 fois la distance Terre-Lune. Il déduit de ces proportions les valeurs suivantes :
- le diamètre lunaire est inférieur à 2/45 distance Terre-Lune et supérieur à 1/30 distance Terre-Lune.
- le diamètre solaire est inférieur à 43/6 diamètres terrestres et supérieur à 19/3 diamètres terrestres.
- le diamètre terrestre est inférieur à 60/19 diamètres lunaires et supérieur à 108/43 diamètres lunaires.
 Remarque
Remarque
Il convient de remarquer qu'à l'époque d'Aristarque les Grecs n'avaient aucune notion de trigonométrie, les premières tables de cordes sont attribuées à Hipparque. C'est pourquoi Aristarque ne tire pas directement la valeur du rapport des distances Terre-Lune et Terre-Soleil de l'angle β, mais encadre cette proportion grâce à des considérations purement géométriques.
On trouve dans la littérature et sur le web de nombreux "exemples" de la détermination de la distance Terre-Lune par Aristarque, avec des hypothèques qui sont très variées (ombre cylindrique, ombre de trois diamètres lunaires, diamètre apparent de la Lune égal à 30'....) et utilisant des méthodes trigonométriques. C'est fort dommage car les méthodes employées par Aristarque sont remarquables et ont un intérêt pédagogique certain.
On peut consulter, sur le site Gallica (gallica.bnf.fr) de la Bibliothèque Nationale, une version française du Traité d'Aristarque de Samos Sur les grandeurs et les distances du Soleil et de la Lune traduite du grec par le Comte de Fortia d'Urban et édité en 1823.
On trouve dans un passage d'Archimède qu'Aristarque a également utilisé la valeur d'une demi-degré pour le diamètre lunaire, l'usage de la valeur de 2° dans le traité Sur la grandeur et la distance du Soleil et de la Lune est parfois présenté comme une valeur hypothétique utilisée par l'auteur dans une démonstration qui se veut plus didactique que physique.
 En savoir plus
En savoir plus
La démonstration suivante est issue de la traduction du Comte de Fortia d'Urban et se trouve dans la proposition VIII du Traité d'Aristarque. Pour rendre la démonstration plus lisible je l'ai retranscrite en termes mathématiques plus contemporains.
La proposition
La proposition VIII est la suivante : La distance à laquelle le soleil se trouve de la terre est plus grande dix-huit fois, mais moindre vingt fois que celle à laquelle la lune se trouve de la terre.
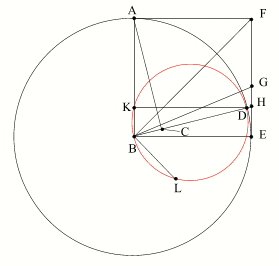
Crédit : IMCCE/Patrick Rocher
La démonstration
Soit A le centre du Soleil, B le centre de la Terre et C le centre de la Lune. Traçons le cercle (c) de centre B et de rayon AB, le rayon BD passant par C et faisant un angle de 3° avec le rayon BE perpendiculaire à BA (l'angle CBE est la trentième partie de l'angle droit). On construit le carré ABEF, ainsi que sa diagonale BF. Soit BG la bissectrice de l'angle EBF.
L'angle CBE est la trentième partie d'un angle droit (90°/30) et l'angle GBE est le quart d'un angle droit (90°/4), donc l'angle GBE vaut les 15/2 de l'angle CBE. Le rapport de EG sur EH est plus grand que le rapport des deux angles GBE et CBE, donc plus grand que 15/2.
BF est la diagonale du carré ABEF, donc le carré de BF est le double du carré de BE. De plus le carré construit sur FG est aussi le double du carré construit sur EG.
Or comme 49 est inférieur au double de 25, le carré de FG/EG = 2 est supérieur à 49/25, le rapport FG/EG est donc supérieur à 7/5.
Donc EF/EG = (EG+GF)/EG = 1 + GF/EG est supérieur à 12/5 ou 36/15.
Ainsi EG/EH est plus grand que 15/2 et EF/EG est supérieur à 36/15, donc EF/EH est supérieur à 18.
Or EF = BE, donc BE/EH est supérieur à 18, et comme BH est supérieur à BE, BH/EH est également supérieur à 18. Or les triangles ABC et EBH sont semblables, donc les rapports BH/EH et AB/BC sont égaux et l'on a bien BA supérieur à 18 BC.
La distance Terre-Soleil est supérieure à 18 fois la distance Lune-Soleil.
Reste à prouver que ce rapport est inférieur à 20. Pour cela traçons la parallèle à BE, cette parallèle coupe AB en K. Traçons le cercle passant par les points BDK et soit L le point du cercle tel que LB soit le côté d'un hexagone inscrit dans ce cercle.
L'angle DBK est égal à l'angle DBE égal à la trentième partie d'un angle droit, l'arc de cercle BK vaut le double donc la quinzième partie d'un angle droit ou encore la soixantième partie de la circonférence.
Or BL est la sixième partie de cette même circonférence; donc l'arc BL est dix fois plus grand que l'arc BK. Or le rapport des cordes BL/BK est inférieur au rapport des arcs BL/BK, donc la corde BL est inférieure à dix fois la corde BK.
Or BD est égal à deux BL, donc BD est inférieur à 20 BK. Or les triangles DKB et ABC sont semblables donc BD/BK = AB/BC, donc AB est bien inférieur à 20 BC.
 Remarque
Remarque
Bien évidemment, si l'on connaît la trigonométrie, cette longue démonstration élégante est remplacée par une simple équation à savoir : AB/BC = 1/sin 3° d'où AB/BC = 19,10.
Ptolémée, dans l'Almageste (livre V chapitre 14), nous décrit deux méthodes permettant de calculer le diamètre apparent de la Lune, puis les distances Terre-Lune et Terre-Soleil.
Le calcul du diamètre lunaire
Pour le calcul du diamètre apparent de la Lune, Ptolémée utilise deux éclipses de Lune observées à Babylone. La première a eu lieu l'an 5 de l'ère de Nabopolassar, qui est l'année 127 de l'ère de Nabonassar, à la fin de la onzième heure du 27 au 28 du mois égyptien Athyr (troisième mois de l'année). Cette date correspond à la nuit du 21 au 22 avril -620 (621 av. J.-C.). Ptolémée nous dit "on vit à Babylone la Lune commencer à s'éclipser; et la plus grande phase de cette éclipse fut du quart du diamètre dans la partie méridionale de l'astre". Puis il calcule la position de la Lune sur son orbite pour l'instant du maximum de l'éclipse et trouve qu'elle se trouve à 9,5° de son nœud et que la distance angulaire entre le centre de la Lune et le centre de l'axe des cônes est de 48,5'. La seconde éclipse de Lune utilisée est celle de l'an 7 de Cambyse, c'est-à-dire l'an 225 de l'ère de Nabonassar, elle s'est produite à une heure avant minuit du 17 au 18 du mois égyptien Phamenoth, ce qui correspond à l'éclipse du 16 juillet -522 (523 av. J.-C.); Ptolémée nous dit "on vit à Babylone la lune s'éclipser de la moitié de son diamètre dans la partie boréale" et il calcule qu'au maximum de l'éclipse la Lune est à 7,8° de son nœud et que la distance angulaire entre le centre de la Lune et le centre de l'axe des cônes est de 40,6'. Ptolémée calcule également que les deux éclipses ont lieu sensiblement lorsque la Lune est à une même distance angulaire de son apogée, donc que les diamètres lunaires apparents sont sensiblement identiques, alors la différence des distances à l'axe des cônes est égale au quart de diamètre lunaire, Ptolémée en déduit que le diamètre lunaire est de l'ordre de 31,3'. À partir de la deuxième éclipse, Ptolémée calcule également le rayon du cône d'ombre en fonction du rayon apparent de la Lune et il trouve que ce rayon "est un peu moindre que le double et 3/5 du rayon de la Lune".
Les tableaux suivants donnent les valeurs calculées avec les théories actuelles et les valeurs données par Ptolémée dans l'Almageste.
L'éclipse des 21 et 22 avril -620
|
Valeurs calculées actuelles |
Valeurs données par Ptolémée |
| Magnitude |
0,1818685 |
|
| Diamètre lunaire apparent |
29,51' |
|
| Instant du maximum |
1h56,2m UT |
|
| Instant du maximum en heure locale |
4h54,2m |
environ 6 h |
| Distance centre de la Lune axe des cônes |
48'31,91" |
48'30" |
| Longitude de la Lune |
204°53'31,5" |
205°32' |
| Elongation par rapport au noeud |
8,77° |
9,3° |
| Longitude par rapport à l'apogée |
339°6' |
340°7' |
L'éclipse du 16 juillet -522
|
Valeurs calculées actuelles |
Valeurs données par Ptolémée |
| Magnitude |
0,5615770 |
|
| Diamètre lunaire apparent |
29,63' |
|
| Instant du maximum |
20h28,8m UT |
|
| Instant du maximum en heure locale |
23h26,8m |
environ 23h |
| Distance centre de la Lune axe des cônes |
37'21,56" |
40'40" |
| Longitude de la Lune |
287°0'41,68" |
288°14' |
| Elongation par rapport au noeud |
6,75° |
7,8° |
| Longitude par rapport à l'apogée |
31°55' |
28°5' |
Ptolémée garde cette valeur de 31' 20" pour le diamètre lunaire et la considère comme constante alors qu'il tient compte des variations de la distance Terre Lune. Il estime le maximum de cette distance à 64 +1/6 rayons terrestres. La valeur moyenne étant de 59 rayons terrestres et il représente le mouvement de la Lune à l'aide d'un cercle déférent de 59 rayons terrestres et d'un épicycle de 5 +1/6 rayons terrestres. En faisant l'hypothèse que le diamètre apparent du Soleil est égal au diamètre apparent de la Lune à son apogée, il déduit de ces valeurs la distance Terre-Soleil et la distance de la Terre au sommet de son cône d'ombre. Il trouve une distance Terre Soleil de 605 rayons terrestres et une distance Terre sommet du cône d'ombre de 134 rayons terrestres.
 Introduction
Introduction
