 Introduction
Introduction
Dans cette section, nous reprenons la notion de Saros et du nombre moyen d'éclipses de Lune dans un Saros. Nous étudions l'évolution des éclipses dans les séries longues d'éclipses homogènes et nous donnons un exemple de série longue d'éclipses.
Le définition du saros et les démonstrations qui lui sont liées ont été traitées dans la partie relative aux éclipses de Soleil. Nous redonnons ici que les particularités propres aux nombres d'éclipses.
Le saros comporte 38 saisons d'éclipses, revenant en moyenne toutes les 5 ou 6 lunaisons. À chaque saison d'éclipses il y a au moins deux éclipses et parfois trois éclipses. En moyenne un saros comprend 84 éclipses, réparties en 42 éclipses de Soleil et 42 éclipses de Lune.
Les 42 éclipses de Lune se répartissent de la manière suivante : 14 éclipses par la pénombre, 28 éclipses par l'ombre dont 14 éclipses partielles et 14 éclipses totales.
Les 42 éclipses de Soleil se répartissent de la manière suivante : 14 éclipses partielles et 28 éclipses centrales.
Ce nombre d'éclipses par saros est une valeur moyenne, en réalité il existe des saros riches pouvant atteindre jusqu'à 94 éclipses (47 de chaque) et des saros pauvres comportant 78 éclipses.
Les canons d'éclipses construits à l'IMCCE comportent 28512 éclipses sur une période de 5999 ans, soit en moyenne 4,7528 éclipses par an et 85,7 éclipses par saros (valeur que l'on peut arrondir à 86). Cette valeur est légèrement plus forte que la valeur moyenne (84). On retrouve le saros moyen du canon d'Oppolzer, construit sur une période plus courte, qui est de 86 éclipses.
Nous avons vu qu'il existe une période de récurrence des éclipses, le saros, qui ramène sensiblement la même éclipse après une période de 6585,32 jours. Ces éclipses séparées par un saros sont appelées éclipses homologues. En réalité, elles ne sont pas parfaitement identiques, mais elles évoluent légèrement d'un saros à l'autre et elles forment des suites qui portent sur de grandes périodes de temps d'où leur nom de suites longues.
Evolution de la longitude de l'opposition après un saros
Nous allons regarder comment évolue la longitude de l'opposition après une période d'un saros. L'écart entre le saros de 223 lunaisons « L » et les 242 révolutions draconitiques « G » est de moins 52 minutes de temps (- 0,03612 jour).
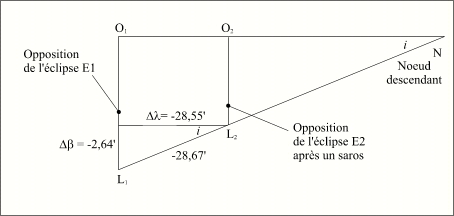
Variation de la longitude de l'opposition entre deux éclipses homogènes
Crédit : IMCCE/Patrick Rocher
Durant ces 52 minutes la Lune, sur son orbite, se déplace en moyenne par rapport à son nœud de -0,03612 x 360°/G = -28,67'. La Lune en opposition se trouve donc déplacée sur son orbite de 28,67' dans le sens rétrograde par rapport au nœud. Compte tenu de l'inclinaison de l'orbite lunaire, ce décalage se traduit par un décalage de la longitude céleste Δλ = -28,55' et par une variation de la latitude céleste de la Lune de Δβ = -2,64'.
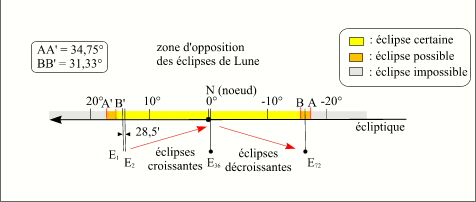
Évolution sur une suite longue d'éclipses
Crédit : IMCCE/Patrick Rocher
Les oppositions des éclipses homologues vont donc parcourir l'arc BB' dans le sens rétrograde avec un pas moyen de 28,55'. Si l'on divise l'arc BB' par 28,55', on constate qu'il peut contenir 66 éclipses et si l'on divise l'arc AA' par 28,55' on voit qu'il peut contenir 74 éclipses. Ces suites d'éclipses sont appelées suites longues. L'étude des canons d'éclipses montre qu'en moyenne ces suites comportent 72 éclipses. Ce qui correspond à une période de temps d'environ 1300 ans.
Aspect d'une suite longue d'éclipse de Lune
Les premières éclipses d'une suite longue sont faibles, car elles sont proches de l'arc A'B', donc loin du nœud. Ensuite, leur grandeur va croître jusqu'à ce qu'elles se produisent au voisinage du nœud, puis leur grandeur va décroître pour finir de nouveau faible au voisinage de l'arc BA. Pour une suite longue de 72 éclipses, si l'on respecte les pourcentages des différents types d'éclipses (environ 1/3 de chaque), on aura donc successivement 12 éclipses par la pénombre de grandeur croissante, puis 12 éclipses partielles par l'ombre, puis 12 éclipses totales de grandeur croissante (sur 650 ans), puis de nouveau 12 éclipses totales de grandeur décroissante, puis 12 éclipses partielles par l'ombre et enfin 12 éclipses par la pénombre de grandeur décroissante (sur 650 ans). Dans la pratique, les deux ou trois éclipses du milieu de la suite longue sont maximales, elles servent de transition entre la période de croissance et de décroissance des éclipses totales. On remarque que toutes les éclipses d'une suite ont lieu au même nœud. Si la suite longue a lieu au nœud descendant les latitudes célestes successives de la Lune croissent des latitudes négatives aux latitudes positives, les positions de la Lune par rapport aux cônes d'ombre et de pénombre de la Terre vont donc se déplacer du sud au nord. Inversement pour une suite longue au nœud ascendant les latitudes célestes successives de la Lune décroissent des latitudes positives aux latitudes négatives, les positions de la Lune par rapport aux cônes d'ombre et de pénombre de la Terre vont donc se déplacer du nord au sud. En réalité, dans les propos précédents, les directions nord et sud désignent le nord et le sud par rapport à l'écliptique et non par rapport à l'équateur terrestre, il faut bien se rappeler que l'écliptique est incliné par rapport à l'équateur terrestre.
Evolution en longitude terrestre
Nous avons vu que la période du saros n'est pas un nombre entier de jours, sa valeur est de 6585,32 jours. Donc entre deux éclipses homologues, la Terre n'a pas tourné d'un nombre entier de jour, les zones concernées par les éclipses ne sont donc pas les mêmes. En 0,32 jour, la Terre tourne d'environ 120°, les zones concernées par l'éclipse se déplacent donc d'environ 120° vers l'ouest. Comme une éclipse de Lune est visible, au moins durant une partie de sa durée, sur environ les deux tiers de la surface terrestre, il n'est pas surprenant que des éclipses homologues successives soient visibles d'un même lieu. Après trois saros, l'éclipse a même lieu sensiblement au même instant. Cela explique que la période de récurrence des éclipses (saros) soit plus facilement décelable, en un lieu, à travers les suites d'éclipses de Lune observées. Ce qui n'est pas le cas pour les éclipses de Soleil.
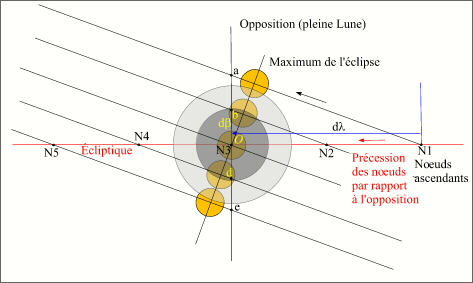
Évolution en latitude
Crédit : IMCCE/Patrick Rocher
Evolution en latitude écliptique par rapport aux cônes d'ombre et de pénombre
Le dessin ci-dessus nous montre l'évolution des éclipses homogènes de Lune durant une suite longue de saros au nœud ascendant. Sur cette figure nous avons figée la longitude de la pleine Lune (opposition), ce sont donc les positions du nœud ascendant qui vont variées dans le sens direct par rapport à l'opposition au cours du temps. Nous avons représenté la position du nœud ascendant environ tous les 325 ans ainsi que les maxima des éclipses correspondantes c'est-à-dire les distances minimales entre le centre de la Lune et le centre des cônes.
Au début de la suite longue d'éclipse de Lune, le nœud se trouve en position N1, à l'ouest de l'opposition, la Lune va donc passer d'ouest en est devant le bord nord du cône de pénombre, les premières éclipses de la suite seront donc des éclipses par la pénombre passant au bord nord de la pénombre (éclipsant donc le sud de la Lune). 325 ans plus tard, le nœud ascendant de l'orbite lunaire est en N2, la Lune rencontre le bord nord du cône d'ombre, les éclipses de Lune sont donc partielles par l'ombre. 325 ans plus tard, le nœud ascendant N3 est confondu avec la longitude de l'opposition, c'est le cas idéal d'une éclipse totale centrale, puis nous avons une situation symétrique par rapport à l'opposition, c'est-à-dire un nœud en N4 correspondant à des éclipses partielles par l'ombre mais au sud du cône d'ombre (éclipsant le nord de la Lune), puis des éclipses par la pénombre au sud du cône de pénombre qui prennent fin après la dernière position N5 du nœud.
On remarque que lorsque le nœud ascendant est à l'ouest de l'opposition le maximum de l'éclipse a lieu avant l'opposition, et que lorsque le nœud ascendant est à l'est de l'opposition le maximum de l'éclipse a lieu après l'opposition. Donc la connaissance de l'instant du maximum de l'éclipse, de l'instant de l'opposition et de la nature du nœud (ascendant ou descendant) permet de situer la position de l'éclipse dans la suite longue d'éclipses homogènes et la partie de la Lune éclipsée. Ou bien, inversement , la connaissance de la position d'une éclipse dans sa suite longue et la nature du nœud permet de savoir si le maximum de l'éclipse a lieu avant ou après l'opposition et de connaître la partie de la Lune éclipsée.
 En savoir plus
En savoir plus
Positions des éclipses d'une saison dans les suites longues de saros
Nous avons vu qu'à chaque saison d'éclipse il y a soit un doublet soit un triplet d'éclipses de Lune et de Soleil. Nous allons essayer de déterminer les positions des éclipses de Lune et de Soleil dans leurs suites longues respectives en fonction de l'allure du triplet ou du doublet d'éclipses. On rappelle que lors d'une saison d'éclipse il y a inversion des nœuds avec la nature des éclipses, ainsi si l'éclipse ou les éclipses de Soleil ont lieu au nœud ascendant l'éclipse ou les éclipses de Lune de la même saison ont lieu au nœud descendant et inversement.
Cas d'un doublet d'éclipses
Dans le cas d'un doublet d'éclipses, l'opposition et la conjonction (les syzygies) sont toujours réparties de part et d'autre des nœuds. Donc l'éclipse correspondant à la syzygie à l'ouest (à droite) du nœud est dans la partie décroissante de sa suite longue et l'éclipse correspondant à la syzygie à l'est (à gauche) du nœud suivant est dans la partie croissante de sa suite longue.
 Exemple
Exemple
Soit un doublet constitué d'une éclipse de Lune au nœud descendant suivie d'une éclipse de Soleil au nœud ascendant. Comme l'éclipse de Lune a lieu avant le passage au nœud, l'opposition est à l'ouest du nœud et l'éclipse de Lune est dans la partie décroissante de sa suite longue (au nœud descendant) et c'est donc la partie sud du disque lunaire qui est éclipsée. L'éclipse de Soleil, elle, a lieu après le passage au nœud, la conjonction est donc à l'est du nœud et l'éclipse de Soleil est dans la partie croissante de sa suite longue (au nœud ascendant), elle sera donc visible dans l'hémisphère nord.
Le tableau ci-dessous résume tous les cas possibles pour un doublet d'éclipses
| Ordre du doublet |
Eclipse de Lune - Eclipse de Soleil |
Eclipse de Soleil - Eclipse de Lune |
| Position de l'éclipse de Lune dans sa suite longue |
partie déroissante |
partie croissante |
| Position de l'éclipse de Soleil dans sa suite longue |
partie croissante |
partie décroissante |
| Eclipse Lune au noeud descendant
Eclipse de Soleil au noeud ascendant |
partie sud du disque lunaire éclipsée
éclipse solaire visible au nord |
partie nord du disque lunaire éclipsée
éclipse solaire visible au sud |
| Eclipse Lune au noeud ascendant
Eclipse Soleil au noeud descendant |
partie nord du disque lunaire éclipsée
éclipse solaire visible au sud |
partie sud du disque lunaire éclipsée
éclipse solaire visible au nord |
Cas d'un triplet d'éclipses
Dans le cas d'un triplet d'éclipses, la première et la troisième éclipses sont de même nature (éclipses de Lune ou éclipses de Soleil) et la seconde éclipse est de nature opposée aux deux autres. La première éclipse appartient à la partie décroissante de sa suite longue et est proche de la fin de cette suite. La troisième appartient à la partie croissante de sa suite longue et est proche du début de cette suite. Pour l'éclipse du milieu, elle est proche du maximum dans sa suite longue, on peut la situer dans la partie croissante ou décroissante de sa suite, uniquement si l'on connaît la position de la syzygie par rapport au nœud, une syzygie à l'ouest du nœud la place dans la partie décroissante et une syzygie à l'est du nœud la place dans la partie croissante de sa suite.
 Remarque
Remarque
Dans les explications ci-dessus, la position à l'ouest (à droite) du nœud est équivalente à une syzygie antérieure au passage au nœud et une position à l'est (à gauche) est équivalente à une syzygie postérieure au passage au nœud. De même nous avons basé nos explications sur les positions relatives des nœuds et des syzygies, nous aurions pu faire les mêmes raisonnements en remplaçant un des deux éléments par la position, ou l'instant, du maximum des éclipses.
Variation sur le fond d'étoile et dans l'année
Nous rappelons que d'un saros à l'autre, le Soleil, donc l'éclipse se décale d'environ 10,5° par rapport aux constellations zodiacales. Au cours d'une suite longue le soleil apparent effectue plus de deux tours complets d'orbite et l'on rencontre toutes les configurations liées au soleil apparent. Les éclipses parcourent les quatre saisons et cela deux fois.
Variation des types d'éclipses
Nous avons vu également que suite à l'écart entre un saros et 239 révolutions anomalistiques, la distance de la Lune à son périgée varie de 2,8° d'un saros à l'autre. Au cours d'une suite longue de 72 saros, les conjonctions lunaires liées aux éclipses homologues (donc la Lune) ne vont parcourir que 202° de l'orbite lunaire, soit un peu plus que la moitié. De plus durant les 48 éclipses centrales du saros, cet arc se réduit à 134°, il convient de comparer cette valeur avec les portions de l'orbite lunaire où les éclipses sont totales ou annulaires.
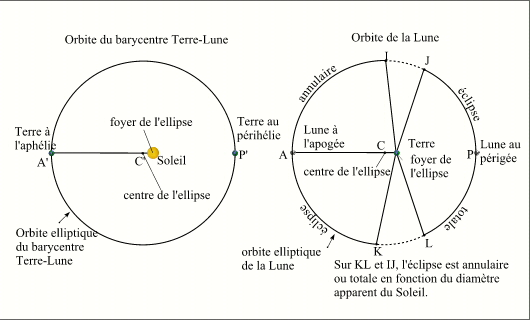
Orbites de la Terre et de la Lune
Crédit : IMCCE/Patrick Rocher
Ainsi si le périgée est proche du milieu de cet arc de 134°, la suite longue est riche en éclipses totales, si au contraire, cet arc avoisine l'apogée la suite longue est riche en éclipses annulaires.
 Remarque
Remarque
Il ne faut jamais perdre de vu que toutes les variations dans les suites longues sont calculées avec des valeurs moyennes et ne sont jamais tout à fait conformes à la réalité. Ainsi le décalage de la conjonction par rapport au nœud de 28,55' est une valeur moyenne. En réalité le Soleil avance plus vite en janvier (il est proche du périgée) qu'en juillet (proche de l'apogée), le calcul montre que la variation de la longitude de la conjonction par rapport au nœud est de l'ordre de 6' en janvier (au lieu de 28,55') et qu'elle atteint 48' en juillet. Les éclipses homologues d'hiver sont donc plus semblables que les éclipses homologues d'été qui évoluent sensiblement plus vite.
Il est facile de connaître la position d'une éclipse dans une suite longue d'éclipses. Les éclipses croissantes ont toujours lieu après le passage au nœud et les éclipses décroissantes ont toujours lieu avant le passage au nœud. La connaissance des instants des syzygies et du passage au nœud permet donc de positionner l'éclipse dans sa suite longue. Inversement la connaissance de la position d'une éclipse dans sa suite longue permet, sauf pour l'éclipse maximale, de savoir sa position par rapport aux nœuds. De plus dans le cas d'un doublet d'éclipses (Lune Soleil ou Soleil Lune) la première éclipse, qui a lieu avant le passage au nœud appartient à la partie décroissante de sa suite longue et la seconde éclipse appartient à la partie croissante de sa suite longue. Dans le cas d'un triplet d'éclipses, la première appartient à la fin de la partie décroissante de la suite longue qui la contient, la dernière appartient au début de la partie croissante de la suite longue qui la contient et l'éclipse médiane se trouve au voisinage du maximum de sa suite longue.
 En savoir plus
En savoir plus
Exemple de suite longue
Le tableau suivant donne la liste des éclipses de la suite longue contenant l'éclipse du 31 mai 2003. On donne successivement le numéro de l'éclipse dans la suite longue, le type d'éclipse, la date de l'éclipse, sa magnitude et la durée maximale de la phase centrale lorsque cette phase existe.
| N° |
type |
date |
magnitude |
durée |
| 1 |
P |
12/10/1624 |
0.0085968 |
|
| 2 |
P |
23/10/1642 |
0.0548679 |
|
| 3 |
P |
03/11/1660 |
0.0896182 |
|
| 4 |
P |
14/11/1678 |
0.1146153 |
|
| 5 |
P |
24/11/1696 |
0.1316624 |
|
| 6 |
P |
07/12/1714 |
0.1419092 |
|
| 7 |
P |
17/12/1732 |
0.1469513 |
|
| 8 |
P |
28/12/1750 |
0.1505860 |
|
| 9 |
P |
08/01/1769 |
0.1530883 |
|
| 10 |
P |
19/01/1787 |
0.1591577 |
|
| 11 |
P |
30/01/1805 |
0.1675941 |
|
| 12 |
P |
11/02/1823 |
0.1857746 |
|
| 13 |
P |
21/02/1841 |
0.2097100 |
|
| 14 |
P |
04/03/1859 |
0.2462690 |
|
| 15 |
P |
15/03/1877 |
0.2919636 |
|
| 16 |
P |
26/03/1895 |
0.3533467 |
|
| 17 |
P |
06/04/1913 |
0.4246662 |
|
| 18 |
P |
17/04/1931 - 18/04/1931 |
0.5110283 |
|
| 19 |
P |
28/04/1949 |
0.6095708 |
|
| 20 |
P |
09/05/1967 |
0.7205292 |
|
| 21 |
P |
19/05/1985 |
0.8411277 |
|
| 22 |
A |
31/05/2003 |
0.9696001 |
03m34.08s |
| 23 |
A |
10/06/2021 |
0.9721316 |
03m47.99s |
| 24 |
A |
21/06/2039 |
0.9730915 |
04m01.45s |
| 25 |
A |
01/07/2057 - 02/07/2057 |
0.9735738 |
04m18.67s |
| 26 |
A |
13/07/2075 |
0.9737206 |
04m40.41s |
| 27 |
A |
23/07/2093 |
0.9737206 |
05m06.77s |
| 28 |
A |
04/08/2111 |
0.9731384 |
05m36.78s |
| 29 |
A |
14/08/2129 - 15/08/2129 |
0.9724857 |
06m09.32s |
| 30 |
A |
26/08/2147 |
0.9716470 |
06m42.98s |
| 31 |
A |
05/09/2165 |
0.9706588 |
07m15.78s |
| 32 |
A |
16/09/2183 - 17/09/2183 |
0.9695596 |
07m46.87s |
| 33 |
A |
28/09/2201 |
0.9684309 |
08m14.61s |
| 34 |
A |
09/10/2219 |
0.9672517 |
08m39.72s |
| 35 |
A |
19/10/2237 |
0.9661547 |
09m00.30s |
| 36 |
A |
30/10/2255 - 31/10/2255 |
0.9651065 |
09m17.21s |
| 37 |
A |
10/11/2273 |
0.9642541 |
09m28.20s |
| 38 |
A |
21/11/2291 |
0.9635287 |
09m34.68s |
| 39 |
A |
02/12/2309 - 03/12/2309 |
0.9630803 |
09m34.31s |
| 40 |
A |
14/12/2327 |
0.9628599 |
09m28.43s |
| 41 |
A |
24/12/2345 |
0.9629606 |
09m15.58s |
| 42 |
A |
04/01/2364 - 05/01/2364 |
0.9633421 |
08m57.77s |
| 43 |
A |
15/01/2382 |
09640683 |
08m34.41s |
| 44 |
A |
26/01/2400 |
0.9651082 |
08m07.46s |
| 45 |
A |
05/02/2418 - 06/02/2418 |
0.9664621 |
07m37.67s |
| 46 |
A |
17/02/2436 |
0.9681073 |
07m06.45s |
| 47 |
A |
27/02/2454 |
0.9700297 |
06m34.42s |
| 48 |
A |
09/03/2472 - 10/03/2472 |
0.9721718 |
06m02.57s |
| 49 |
A |
21/03/2490 |
0.9745093 |
05m31.07s |
| 50 |
A |
01/04/2508 |
0.9769654 |
05m00.43s |
| 51 |
A |
12/04/2526 - 13/04/2526 |
0.9795505 |
04m29.66s |
| 52 |
A |
23/04/2544 |
0.9821258 |
03m59.66s |
| 53 |
A |
04/05/2562 |
0.9847154 |
03m29.01s |
| 54 |
A |
14/05/2580 -15/05/2580 |
0.9871679 |
02m58.81s |
| 55 |
A |
26/05/2598 |
0.9895234 |
02m27.78s |
| 56 |
A |
06/06/2616 |
0.9916211 |
01m58.16s |
| 57 |
A |
17/06/2634 |
0.9935042 |
01m29.84s |
| 58 |
A |
27/06/2652 - 28/06/2652 |
0.9950354 |
01m05.79s |
| 59 |
A |
09/07/2670 |
0.9961687 |
00m47.26s |
| 60 |
A |
19/07/2688 |
0.9967399 |
00m36.25s |
| 61 |
A |
31/07/2706 -01/08/2706 |
0.9960352 |
00m.36.88s |
| 62 |
P |
11/08/2724 |
0.8822576 |
|
| 63 |
P |
22/08/2742 |
0.7560645 |
|
| 64 |
P |
01/09/2760 |
0.6399250 |
|
| 65 |
P |
13/09/2778 |
0.5318151 |
|
| 66 |
P |
23/09/2796 |
0.4338706 |
|
| 67 |
P |
04/102814 |
0.3469499 |
|
| 68 |
P |
15/10/2832 |
0.2725393 |
|
| 69 |
P |
26/10/2850 |
0.2098505 |
|
| 70 |
P |
05/11/2868 |
0.1587829 |
|
| 71 |
P |
17/11/2886 |
0.1194801 |
|
| 72 |
P |
28/11/2904 |
0.0907818 |
|
| 73 |
P |
09/12/2922 |
0.0696946 |
|
| 74 |
P |
20/12/2940 |
0.0570489 |
|
| 75 |
P |
31/12/2958 |
0.0487713 |
|
| 76 |
P |
10/01/2977 |
0.0452276 |
|
| 77 |
P |
22/01/2995 |
0.0403169 |
|
On remarque que cette suite n'est pas complète, en effet le canon d'éclipse de l'IMCCE s'arrête en 2999, il y a probablement des éclipses de la suite qui sont postérieures à cette date. Malgré cela on dépasse la valeur moyenne de 72 éclipses. Et l'on est assez loin des valeurs moyennes, ainsi le nombre d'éclipses partielles de la partie croissante est de 21, la moyenne donne 12 ! On constate également que toutes les éclipses centrales sont des éclipses annulaires, donc l'arc parcouru par les conjonctions lunaires est au voisinage de l'apogée. L'éclipse du 31 mai 2003 est la première éclipse centrale de la partie croissante de la suite, on peut donc en déduire qu'elle a lieu après le passage au nœud et relativement longtemps après ce passage. De plus elle est proche d'un des pôles terrestre. On ne peut pas savoir si la suite est au nœud ascendant ou descendant de l'orbite lunaire. Pour cela il suffit de connaître la latitude de la Lune à la conjonction pour une seule éclipse de la suite. Cette longitude est positive pour l'éclipse du 31 mai donc cette suite longue est au nœud ascendant et l'éclipse du 31 mai 2003 est proche du pôle nord terrestre et les éclipses de la suite vont parcourir le globe terrestre du nord au sud.
Les éphémérides de la Lune nous donnent les informations suivantes :
- le 28/05/2003 à 13h 04m 44s UT : la Lune à l'apogée (distance maximale à la Terre) d=406168 km, diam. app. =29.5'.
- le 30/05/2003 à 08h 32m 17s UT : la Lune passe par le nœud ascendant de son orbite, long. moyenne = +59° 30,9'.
- le 31/05/2003 à 04h 08m 18s UT : maximum de l'éclipse annulaire de Soleil.
- le 31/05/2003 à 04h 19m 51s UT : Nouvelle Lune.
On constate que le maximum de l'éclipse a bien lieu entre le passage et la conjonction, qu'il est proche de la conjonction (11m 33s) mais éloigné du passage au nœud (19h 36m 1s). L'éclipse est proche du passage de la Lune à l'apogée elle est donc annulaire.
 Introduction
Introduction


