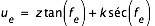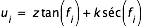Introduction
Dans cette section nous allons décrire les circonstances locales d'une éclipse. C'est-à-dire ce que voit un observateur à la surface de la Terre. Dans ce cas on regarde le Soleil et la Lune (et non la Terre et l'ombre de la Lune). L'observateur en fonction de sa position, verra ou ne verra pas d'éclipses. Dans le cas d'une éclipse centrale, suivant sa position, il verra la phase centrale ou non.
La partie pour en savoir plus est complexe et demande une bonne connaissance du calcul numérique.
Il ne faut pas les confondre avec les circonstances générales décrites dans le paragraphe précédent. Les circonstances locales d'une éclipse décrivent, en un lieu donné, les différentes phases de l'éclipse, observables par un observateur situé en ce lieu.
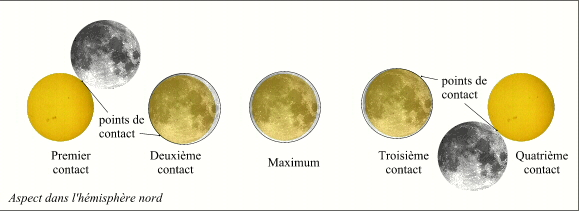
Phases locales d'une éclipse totale.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé dans la bande de totalité durant une éclipse totale de Soleil, pour rendre le dessin plus lisible nous avons ajouté une transparence à la Lune durant la totalité pour permettre de voir la position du Soleil occulté par la Lune. La durée de la phase de totalité en ce lieu est égale à l'intervalle de temps séparant les second et troisième contacts. La durée de l'éclipse locale (phases partielles et phase totale) est égale à l'intervalle de temps séparant les premier et quatrième contacts. Les points de Baily apparaissent au voisinage des deuxième et troisième points de contacts.
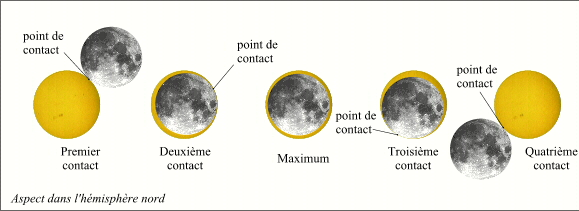
Phases locales d'une éclipse annulaire.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé dans la bande de centralité d'une éclipse annulaire. La durée de la phase annulaire en ce lieu est égale à l'intervalle de temps séparant les second et troisième contacts. La durée de l'éclipse locale (phases partielles et phase annulaire) est égale à l'intervalle de temps séparant les premier et quatrième contacts.
Phases locales d'une éclipse partielle.
Crédit : IMCCE/Patrick Rocher
Le dessin ci-contre nous montre les différentes phases observables par un observateur situé sur le trajet du cône de pénombre d'une éclipse. L'éclipse peut être partielle, annulaire ou totale. Dans les deux derniers cas, l'observateur n'est pas dans la bande de centralité, il observe donc l'éclipse annulaire ou totale sous la forme d'une éclipse partielle. La durée de l'éclipse locale (phase partielle) est égale à l'intervalle de temps séparant les premier et quatrième contacts.
Ces phases sont les suivantes :
- le début de l'éclipse partielle, appelé également premier contact (parfois premier contact extérieur),
- le début de l'éclipse totale ou annulaire (si l'observateur est dans la bande de centralité), appelé également deuxième contact (parfois premier contact intérieur),
- le maximum de l'éclipse, instant où la grandeur est maximum en ce lieu,
- la fin de l'éclipse totale ou annulaire (si l'observateur est dans la ligne de centralité), appelée également troisième contact (parfois deuxième contact intérieur),
- la fin de l'éclipse partielle, appelée également quatrième contact (parfois deuxième contact extérieur).
Pour chacun des contacts, en plus des instants du contact, on donne à l'observateur l'angle au pôle
P et l'angle au zénith Z. On remarquera que les points des contacts intérieurs des éclipses totales sont diamétralement opposés aux points des contacts intérieurs des éclipses annulaires.
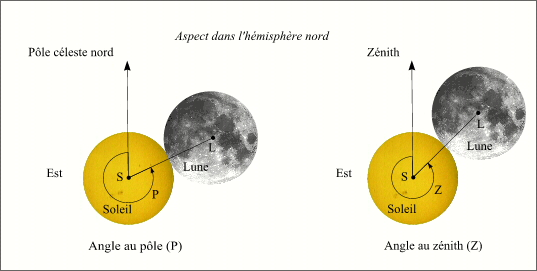
Définitions des angles au pôle et au zénith
Crédit : IMCCE/Patrick Rocher
L'angle au pôle P d'un contact est l'angle de la direction nord N (partie boréale du cercle horaire du centre S du Soleil) avec l'arc de grand cercle joignant les centres S et L du Soleil et de la Lune, compté positivement vers l'est, dans le sens nord-est-sud-ouest.
L'angle au zénith Z d'un contact a une définition analogue à celle de P, en remplaçant le cercle horaire du centre S du Soleil par le vertical du même point.
Remarques
Sous nos latitudes (en France) et pour les latitudes positives situées au-dessus du tropique du Cancer (latitudes supérieures à 23°), le Soleil passe au méridien au sud, donc quand on regarde le Soleil, l'ouest est à droite du Soleil et l'est est à sa gauche. La Lune éclipse le Soleil d'ouest en est (donc de la droite vers la gauche lorsque l'on regarde le Soleil). Pour les latitudes négatives situées sous le tropique du Capricorne (latitudes inférieures à -23°), le Soleil passe au méridien au nord, l'aspect du phénomène est inversé, l'éclipse a, bien évidemment, toujours lieu d'ouest en est, mais elle a lieu de la gauche vers la droite car on regarde le Soleil vers le nord. Dans la zone intertropicale les deux cas de figure sont possibles, cela dépend de la date de l'éxclipse et du lieu d'observation. La connaissance des instants et positions du deuxième et du troisième point de contact est très importante pour les éclipses totales de Soleil, car elle indique quand et où vont apparaître les points de Baily.
Avec l'instant du maximum on donne également la grandeur de l'éclipse, le degré d'obscuration, la hauteur h et l'azimut a du Soleil.
La hauteur h du Soleil sur l'horizon est l'angle de la direction du Soleil et du plan horizontal, compté en degrés de -90° à +90°.
L'azimut est l'angle formé par la projection de la direction du Soleil dans le plan horizontal avec la direction du Sud, compté en degré dans le sens rétrograde (sud = 0°, ouest = 90°, nord = 180°, est = 270°).
Les circonstances locales d'une éclipse peuvent être calculées à l'aide des éléments de Bessel
En savoir plus
Au XIXe siècle, l'astronome allemand Friedrich Bessel (1784-1846) a mis au point une méthode, toujours utilisée de nos jours, pour faciliter le calcul des circonstances locales et générales d'une éclipse de Soleil.
Pour un lieu donné il y a lieu de déterminer :
- les instants des différents contacts,
- l'instant du maximum de l'éclipse et la grandeur de l'éclipse à cet instant,
- les angles au pôle et au zénith de chacun des contacts.
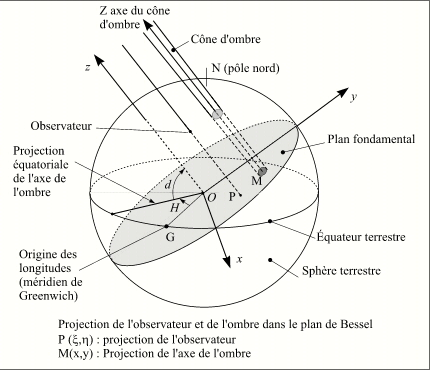
Les éléments de Bessel.
Crédit : IMCCE/Patrick Rocher
Le lieu d'observation est défini par sa longitude λ (positive à l'ouest et négative à l'est du méridien de Greenwich), sa latitude ϕ et son altitude h au-dessus du niveau de la mer.
On définit à chaque instant un système de coordonnées Oxyz de sens direct, dans lequel :
O est le centre de la Terre.
L'axe Oz est parallèle à l'axe des cônes de pénombre et d'ombre, le sens positif étant celui qui va de la Terre à la Lune.
L'axe Ox est l'intersection du plan fondamental Oxy perpendiculaire à Oz et du plan de l'équateur terrestre, le sens positif étant vers l'est.
L'axe Oy est normal à Ox dans le plan fondamental, le sens positif étant vers le nord.
En savoir plus
En utilisant comme unité de longueur le rayon équatorial terrestre, les éléments de Bessel sont définis de la manière suivante :
x, y, z sont les coordonnées du centre de la Lune.
d et H sont la déclinaison de l'axe Oz et son angle horaire par rapport au méridien de Greenwich.
fe et fi sont les demi-angles au sommet des cônes de pénombre et d'ombre, fe étant pris par convention positif et fi négatif.
ue et ui sont les rayons des sections circulaires des cônes de pénombre et d'ombre par le plan fondamental Oxy et s'obtiennent par les formules suivantes :
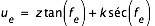
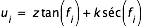
où k est le rayon de la Lune exprimé en rayon équatorial terrestre.
En savoir plus
Les coordonnées ξ, η, ζ du lieu d'observation dans le système Oxyz sont :
ξ = ρ . cos ϕ ' . sin (H - λ ),
η = ρ . sin ϕ ' . cos d - ρ . cos ϕ ' . sin d . cos ( H - λ ),
ζ = ρ . sin ϕ ' . sin d + ρ . cos ϕ ' . cos d . cos ( H - λ ),
avec :
ρ . cos ϕ ' = cos u + h/r0 . cos ϕ
ρ . sin ϕ ' = (1 - f) . sin u + h/r0 . sin ϕ
et
tan u = (1 - f) . tan ϕ
où h est l'altitude du lieu exprimée en mètres, r0 est le rayon équatorial terrestre exprimé en mètres et f l'aplatissement de l'ellipsoïde terrestre (f = 1/298,257 = 0,003 35281).
En savoir plus
Les variations horaires ξ ', η ', ζ ' de ces coordonnées sont fournies avec une précision de l'ordre de la seconde de temps par les formules suivantes, H' étant exprimé en radians par heure.
ξ ' = H' . ρ . cos ϕ ' . cos (H - λ ),
η ' = H' . ξ . sin d,
ζ ' = - H' . ξ . cos d,
Les rayons le et li des sections circulaires des cônes de pénombre et d'ombre par le plan mené par le lieu d'observation parallèlement au plan fondamental s'obtiennent par les formules suivantes :
le =ue - ζ tan fe
li = ui - ζ tan fi
En savoir plus
Chaque élément de Bessel que l'on pourra désigner par b est représenté sur un intervalle de temps (t0, t1) par des coefficients de développements en polynômes du temps, à l'exception de tan fe et de tan fi qui sont considérées comme constantes sur l'intervalle. Un élément de Bessel se calcule à un instant t par la formule :
b = b0 + b1 . T + b2 . T2 + b3 . T3
avec T = t - t0.
T, exprimé en heure, représente le temps écoulé depuis l'instant origine t0.
La variation horaire b' d'un élément de Bessel se calcule par la formule :
b' = b1 + 2 b2 . T + 3 b3. T2
En savoir plus
Soient :
U = x - ξ , U' = x' - ξ',
V = y - η , V' = y' - η ',
On prend comme valeur de départ td l'époque du maximum de l'éclipse, l'instant du maximum tm se calcule en ajoutant à td la valeur Dtm donnée par :
Dtm = - (UU' + VV') / (U'2+ V'2)
On doit réitérer le calcul en prenant comme nouvelle valeur de départ la valeur de tm.
La grandeur maximale est donnée par :
g = (le - lm) / (le - li)
pour une éclipse annulaire ou totale au lieu considéré, où :
g = (le - lm) / (2 le- 0,5465) pour une éclipse partielle, avec :
lm = (U2 + V2)1/2
En savoir plus
On prend comme valeurs de départ td du premier et du quatrième contacts (contacts extérieurs) des valeurs approchées déduites de la carte de l'éclipse et l'on prend comme valeurs de départ du second et du troisième contacts (contacts intérieurs), lorsqu'ils existent, la valeur tm du maximum calculée précédemment.
Pour chaque valeur td de départ on calcule les quantités suivantes :
β = (UU' + VV') / (U'2 + V'2),
γ = (U2 + V2 - l2) / (U'2 + V'2),
θ = ±(β2 - γ)1/2
avec l = le ou l = li et θ étant du signe de β.
Les instants du premier et du quatrième contacts se calculent par la formule :
t = td - β + θ
et les instants du second et du troisième contacts se calculent par les formules :
t = td - β - |θ| pour le second contact,
et
t = td - β + |θ| pour le troisième contact.
Comme pour le calcul du maximum on doit réitérer les calculs en prenant comme nouvelles valeurs de départ les valeurs t.
En savoir plus
La valeur de l'angle au pôle P d'un point de contact est donnée par :
tan P = U/V ,
où sin P a le signe de U, sauf pour les second et troisième contacts (contacts intérieurs) d'une éclipse totale pour lesquels sin P est de signe contraire à U.
L'angle au zénith Z d'un point de contact est donné par :
Z = P - Γ ,
en désignant par Γ l'angle parallactique défini d'une façon approchée par :
tan Γ = ξ/η ,
sin Γ étant du signe de ξ.