En raison des mouvements orbitaux de la Terre et de la Lune, les distances Terre-Lune et Soleil-Terre ne sont pas constantes, les diamètres apparents de la Lune et du Soleil sont donc variables. Le diamètre apparent de la Lune est maximal lorsque la Lune est proche de la Terre donc à son périgée, et il est minimal lorsque la Lune est loin de la Terre donc à son apogée. De même le diamètre apparent du Soleil est maximal lorsqu'il est proche de la Terre donc lorsque le Soleil apparent est à son périgée ou la Terre est à son périhélie (actuellement vers le 4 janvier) et le diamètre apparent du Soleil est minimal lorsque le Soleil est loin de la Terre, donc lorsque le Soleil apparent est à l'apogée ou la Terre à l'aphélie (actuellement vers le 4 juillet).

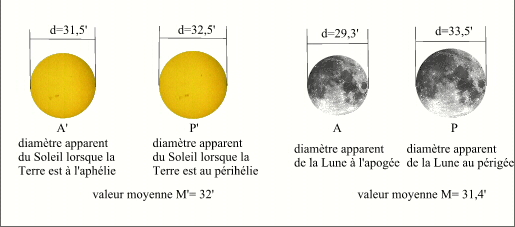
Valeurs extrêmes et moyennes des diamètres apparents du Soleil et de la Lune.

Crédit : IMCCE/Patrick Rocher

Comme on le constate sur la figure ci-contre le diamètre apparent moyen de la Lune est plus petit que le diamètre apparent moyen du Soleil, on peut donc s'attendre à avoir en moyenne plus d'éclipses annulaires que d'éclipses totales.

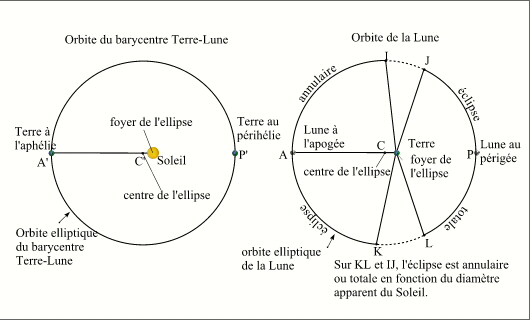
Analyse des types d'éclipses solaire en fonction des positions orbitales de la Terre et de la Lune.

Crédit : IMCCE/Patrick Rocher

Comme nous venons de le voir, nous pouvons calculer les valeurs extrêmes des diamètres apparents de la Lune et du Soleil vus depuis la Terre. Nous allons affiner un peu notre étude, en effet nous pouvons déterminer la portion de l'orbite lunaire sur laquelle le diamètre apparent de la Lune est toujours plus grand que le plus grand diamètre apparent du Soleil (32,5'), c'est l'arc d'orbite LJ sur la figure ci-contre. Sur cette portion d'orbite lunaire les éclipses centrales sont toujours totales, quelle que soit la position de la Terre sur son orbite. Nous pouvons également déterminer la portion de l'orbite lunaire sur laquelle la Lune a un diamètre apparent toujours plus petit que le plus petit diamètre apparent du Soleil (31,5'), c'est l'arc d'orbite IK sur la figure ci-contre. Sur cette portion d'orbite les éclipses centrales sont toujours annulaires quelle que soit la position de la Terre sur son orbite. Sur les portions d'orbites IJ et KL le diamètre apparent de la Lune varie entre 31,5' et 32,5' (valeurs extrêmes du diamètre apparent du Soleil) le type de l'éclipse centrale est donc déterminé par le diamètre apparent du Soleil donc par la position de la Terre sur son orbite. C'est sur ces portions de l'orbite de la Lune que l'on trouve les éclipses mixtes.

On remarquera que sur la figure ci-contre, les orbites de la Terre et de la Lune sont représentées par des cercles, cela est totalement justifié compte tenu des faibles excentricités des orbites lunaire et terrestre. Par contre les corps centraux ne sont pas aux centres des cercles mais sont excentrés. On notera également que l'arc LJ est centré sur le périgée de la Lune, donc les éclipses avec la Lune au périgée sont toujours des éclipses totales, de même l'arc IK est centré sur l'apogée de la Lune donc les éclipses avec la Lune en apogée sont toujours des éclipses annulaires. Enfin l'arc IK est plus grand que l'arc LJ, cela confirme le fait qu'il y ait en moyenne plus d'éclipses annulaires que d'éclipses totales.

Nous pouvons avoir une autre approche du problème en considérant les distances Soleil-Lune et Lune-Terre, en effet il y a équivalence entre les diamètres apparents et les distances des corps entre eux.

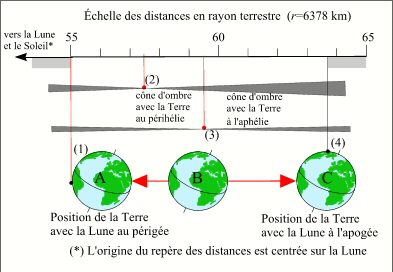
Positions extrêmes pour les éclipses centrales de Soleil.

Crédit : IMCCE/Patrick Rocher

• (1) est la distance observateur-Lune minimale, d=55,0 rayons terrestres, c'est-à-dire avec la Lune au périgée et l'observateur avec la Lune au zénith,
• (4) est la distance observateur-Lune maximale, d=63,8 rayons terrestres, c'est-à-dire avec la Lune à l'apogée et l'observateur avec la Lune à l'horizon,
• (2) correspond à une distance Lune sommet du cône d'ombre de longueur minimale, l=57,5 rayons terrestres, c'est à dire une distance Soleil-Terre minimale donc un Soleil au périgée (ou la Terre au périhélie),
• (3) correspond à une distance Lune sommet du cône d'ombre de longueur maximale, l=59,5 rayons terrestres, c'est-à-dire une distance Soleil-Terre maximale donc un Soleil à l'apogée (ou la Terre à l'aphélie).

Positions extrêmes pour les éclipses centrales de Soleil.

Crédit : IMCCE/Patrick Rocher

Cette figure donne les distances extrêmes de la Terre et du cône d'ombre, en fonction des positions extrêmes de la Lune, du Soleil et de la Terre. L'origine des distances est le centre de la Lune et les distances sont exprimées en rayons terrestres. La distance observateur-Lune varie de 55 à 63,8 rayons terrestres. La distance entre la Lune et le sommet du cône d'ombre varie, elle, de 57 à 59,5 rayons terrestres. Cette figure nous montre que si, au moment de l'éclipse, on est dans la position A, c'est-à-dire avec la Lune au périgée, alors quelle que soit la position de la Terre sur son orbite, l'éclipse est totale car la Terre coupe toujours le cône d'ombre avant son sommet. De même si, au moment de l'éclipse, on est en position C, c'est-à-dire avec la Lune à son apogée, alors quelle que soit la position de la Terre sur son orbite l'éclipse est annulaire car la Terre coupe toujours le prolongement de l'ombre. En faisant varier la position de la Terre (par rapport à la Lune) entre ces deux positions, on peut visualiser tous les cas intermédiaires possibles. Par exemple, lorsque la Terre est en B (distance Lune-Terre = 59 r), si la Terre est au périhélie (cône d'ombre en position 2) l'éclipse est annulaire car la Terre coupe le prolongement du cône d'ombre, si la Terre est à son l'aphélie (cône d'ombre en position 3) alors l'éclipse est totale car la Terre coupe le cône d'ombre, avec un cône d'ombre entre les positions 2 et 3 toutes les configurations sont possibles (éclipses totales, annulaires ou mixtes).