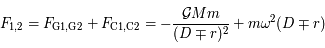
D'après ce qui précède, le bilan dans le référentiel tournant s'écrit:
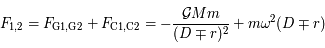
On peut en déduire 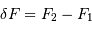 :
:
![\begin{eqnarray*} \delta F& =& F _{\mathrm{G2}} + F _{\mathrm{C2}} - (F _{\mathrm{G1}} + F _{\mathrm{C1}})\\ & =& -{\cal G}Mm\left[{1\over (D-r)^{2}} - {1\over (D+r)^{2}}\right] + m\omega^{2}(D-r-D-r)\\ & =& -{{\cal G}Mm\over D^{2}}\left[\left(1-{r\over D}\right)^{-2}-\left(1+{r\over D}\right)^{-2}\right]-2mr\omega^{2}\\ &\simeq & -{{\cal G}Mm\over D^{2}}\left[\left(1+2{r\over D}\right)-\left(1-2{r\over D}\right)\right]-2mr\omega^{2}\ \mathrm{ car }\ r\ll D\\ &\simeq & -{4{\cal G}Mmr\over D^{3}} - 2mr\omega^{2}\\ &\simeq & -{6{\cal G}Mmr\over D^{3}}\ \mathrm{ car}\ \omega\ = \displaystyle{\left({{\cal G}M\over D^{3}}\right)^{1/2}}\\ \end{eqnarray*}](../pages_effet-de-maree/equations_limite-roche/equation59.png)
Dans la cadre du modèle, cette force différentielle rend compte de l'effet de marée entre les 2 composantes du satellite.