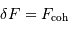 , pour une distance
, pour une distance 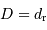 qui provient de :
qui provient de :
Le satellite est à la limite de Roche quand on a l'égalité
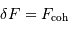 , pour une distance
, pour une distance 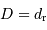 qui provient de :
qui provient de :
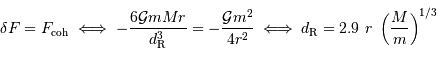
Comme
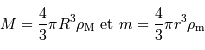
Alors
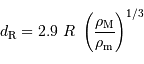
La valeur observée de la limite de Roche est 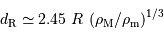 .
Elle croît avec le rayon et la masse volumique de la planète.
.
Elle croît avec le rayon et la masse volumique de la planète.