Les éphémérides
Auteur: Jean-Eudes Arlot
- Introduction
- Qu'est-ce qu'une éphéméride ?
- Modèles théoriques des mouvements
- Histoire des éphémérides
- Les différents types d'éphémérides
- Les éphémérides de position
- Ephémérides pour les observations physiques
- Le repérage des éphémérides de position
- Les systèmes de référence
- Les repères de référence célestes
- Les repères cinématiques liés aux étoiles
- Les repères dynamiques liés aux corps du système solaire
- Les systèmes de coordonnées
- Représentation des éphémérides
- Les éphémérides sous forme de tables
- En savoir plus: l'interpolation des éphémérides
- Les éphémérides sous forme graphique
- Détermination de la configuration des satellites de Jupiter à une date donnée
- Approximation d'une fonction par un polynôme
- En savoir plus: approximation de Tchebychev (1)
- En savoir plus: approximation de Tchébychev (2)
- En savoir plus: approximation de Tchébychev (3) exemple de calcul
- En savoir plus: approximation par des fonctions mixtes (1)
- En savoir plus: approximation par des fonctions mixtes (2)
- En savoir plus: Exemple de calcul
- La précision des éphémérides
- Les phénomènes astronomiques
- Qu'est-ce qu'un phénomène astronomique ?
- Lever et coucher d'un astre en un lieu donné
- Calcul d'un coucher ou d'un lever d'un astre
- Les phénomènes des satellites de Jupiter
- Où se procurer des éphémérides
- Où trouver des éphémérides imprimées ?
- Où trouver des éphémérides sur Internet ?
- Comment faire ses propres éphémérides ?
Introduction
 Introduction
Introduction
Dans le langage courant, l'éphéméride désigne ce qui se passe journellement ; l'éphéméride du jour est la liste des événements marquants de ce jour. Par extension, les éphémérides astronomiques désignent a priori une table journalière de positions de corps célestes mobiles (ceux du système solaire) ainsi que des phénomènes astronomiques ayant lieu ce jour telles les éclipses. Les éphémérides de positions sont donc avant tout la représentation d'un mouvement. Les éphémérides que l'on connaît sous forme de tables de nombres sont les plus courantes et les plus anciennes, mais ce n'est pas la seule forme possible et, de nos jours, ce n'est plus la forme la meilleure car il en existe maintenant d'autres beaucoup plus performantes.
Pour obtenir une éphéméride, il est nécessaire de disposer :
- d'un modèle théorique (dynamique ou cinématique) du mouvement du corps considéré ;
- d'observations de ce corps pour ajuster le modèle ;
- d'une représentation du mouvement pour donner les positions souhaitées à l'utilisateur.
La qualité d'une éphéméride pour la représentation d'un mouvement dépend de deux facteurs : utiliser un petit nombre de données (éviter des tables gigantesques) et ensuite avoir une bonne précision (commettre l'erreur la plus faible possible par rapport à la position "vraie" que l'on veut décrire).
Qu'est-ce qu'une éphéméride ?
Modèles théoriques des mouvements
Depuis les débuts de l'astronomie, modéliser le mouvement des corps du système solaire a toujours été un défi. Il s'est agi tout d'abord d'extrapolations empiriques des observations réalisées ; les premières tables proviennent ainsi d'une analyse purement cinématique des mouvements observés. La précision de ces premières tables est évidemment médiocre et ne progresse qu'avec l'amélioration de la précision des observations.
Viennent ensuite des prédictions fondées sur des théories gravitationnelles dont les paramètres sont déduits d'observations. A partir de Newton, les lois dynamiques sont connues et il importe alors de mettre en équation et de tenir compte de tous les effets gravitationnels qui peuvent agir sur les corps. Les recherches théoriques de Lagrange relatives au problème planétaire ont conduit à modéliser l'évolution à long terme des orbites par un système différentiel linéaire qui couple les excentricités et les inclinaisons. C'est un résultat fondamental. On consultera les cours relatifs aux lois de Kepler et à la mécanique céleste pour approfondir ces notions.
Histoire des éphémérides
Des recueils de prédictions diverses liées au calendrier, appelés almanachs ou éphémérides existaient dès le XIVème siècle. Citons :
- les tables alphonsines, faites sur l'ordre d'Alphonse X de Castille à partir de l'Almageste vers 1250 et qui arrivèrent à Paris en 1320 ;
- les éphémérides de Regiomontanus couvrant les années 1475-1506 ;
- les tables pruténiques construites en 1551 par Reinhold sur la base des travaux de Copernic ;
- les éphémérides des satellites de Jupiter de Simon Marius en 1614 ;
- les tables rudolphines en 1627 construites sur la base des travaux de Kepler et Tycho Brahé.
Les premières éphémérides vraiment destinées aux astronomes pour faire progresser notre connaissance du système solaire et de la Terre apparurent avec la Connaissance des Temps dont le premier volume parut à Paris en 1679. Ce premier volume se bornait à annoncer aux astronomes les principaux phénomènes et à leur fournir les calculs nécessaires aux réductions de leurs observations journalières. On y trouvait les levers et couchers du Soleil, de la Lune et des cinq planètes connues, Mercure, Vénus, Mars, Jupiter et Saturne, leurs passages au méridien de Paris, leurs longitudes, leurs latitudes et leurs déclinaisons. Au XVIIIème siècle, Lalande construisit ensuite les tables du Soleil et des planètes qui servirent de base aux éphémérides publiées dans la Connaissance des Temps jusqu'en 1808. En 1767 paraît à Londres le Nautical Almanac and Astronomical Ephemeris, éphéméride de même nature destinée également à contribuer à l'amélioration de l'astronomie, de la Géographie et de la Navigation.
Au cours des années 1770-1825, Laplace étudie les conséquences de l'application de la loi de la gravitation de Newton sur le mouvement des corps du système solaire et résout plusieurs problèmes concernant les théories planétaires. La plupart des tables du Soleil et des planètes utilisées dans la Connaissance des Temps durant la première moitié du XIXème siècle, sont issues de ses travaux.
La représentation de ces éphémérides a évolué au cours du temps. Jusqu'à la fin du XVIIIème siècle, la Connaissance des Temps présentait les éphémérides des astres mois par mois, le Soleil de jours en jours et les planètes de six jours en six jours. A partir de 1838, les éphémérides sont publiées corps par corps. Elles sont journalières pour le Soleil, de trois jours en trois jours pour Mercure, de six jours en six jours pour Vénus et Mars, de huit jours en huit jours pour Jupiter, de dix jours en dix jours pour Saturne et de quinze jours en quinze jours pour Uranus. En 1863, les éphémérides deviennent journalières pour Mercure, Vénus, Mars, Jupiter et Saturne et de quatre jours en quatre jours pour Uranus et Neptune.
Les éphémérides ont subi de nos jours d'importantes transformations. En 1980, la présentation des éphémérides sous forme de tables interpolables a été remplacée par une représentation en polynômes de Tchebychev beaucoup plus compacte et bien adaptée au développement de la micro-informatique.
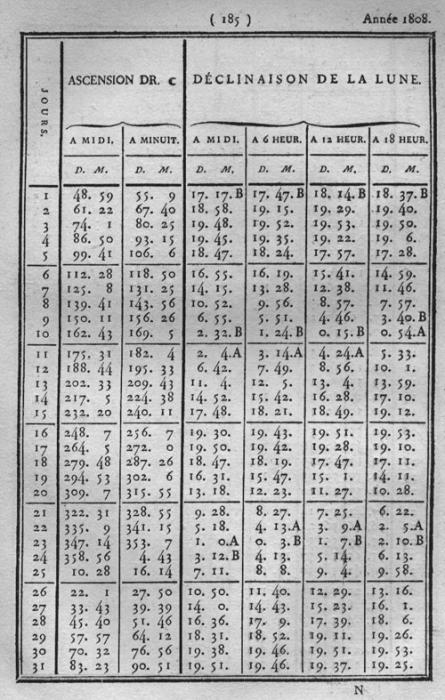
L'ascension droite et la déclinaison de la Lune dans la Connaissance des Temps pour l'année 1808.
Les valeurs sont données de 12h en 12h pour l'ascension droite et de 6h en 6h pour la déclinaison. La précision reste faible du fait de la rapidité du mouvement de la Lune.
Crédit :
Bureau des Longitudes
Les différents types d'éphémérides
Les éphémérides de position
Selon la quantité à représenter dans les éphémérides, on est amené à choisir un plan fondamental et des coordonnées. Pour les éphémérides destinées à l'observateur terrestre, le plan fondamental sera l'équateur terrestre et on fournira l'ascension droite (angle compté habituellement en heures vers l'est à partir de l'équinoxe de 0 à 24 heures, le long de l'équateur terrestre) et la déclinaison (angle compté habituellement en degrés vers le nord au-dessus du plan équatorial). On donne aussi le rayon vecteur, distance du centre du repère à l'astre considéré : il ne dépend pas du repère, sauf en ce qui concerne la prise en compte du temps de lumière.
Les éphémérides de la Lune, du Soleil et des planètes principales donnent des coordonnées apparentes pour le pointage des télescopes. Pour Pluton, les astéroïdes et les comètes, on donne les coordonnées astrométriques directement comparables aux catalogues d'étoiles. Dans le cas des satellites naturels proches des planètes, on donne des coordonnées tangentielles relatives à la planète dans un plan tangent à la sphère céleste, directement comparables aux clichés photographiques ou aux images provenant des caméras CCD.
Citons aussi les coordonnées topocentriques, centrées sur un observateur situé sur la surface terrestre : ces coordonnées ne peuvent être que calculées à la demande et on passe en général des coordonnées apparentes aux coordonnées topocentriques par une petite correction si nécessaire.
Certaines positions sont données dans des coordonnées non pas sphériques mais rectangulaires, l'axe X étant dirigé vers l'équinoxe du repère et l'axe Z vers le pôle nord céleste de ce repère. Des éphémérides données ainsi sont plutôt destinées à la navigation spatiale.
Ephémérides pour les observations physiques
Pour observer de la Terre à un instant donné des points situés à la surface d'un astre du système solaire, il faut définir les paramètres qui caractérisent la rotation de l'astre autour de son axe, donner leurs valeurs numériques et définir les systèmes de coordonnées par rapport auxquels ces points seront repérés sur cet astre (repère planétographique). On calcule ensuite les données qui permettent de connaître quels sont les points de l'astre qui sont visibles de la Terre à l'instant considéré. Il est également utile de connaître des quantités liées à l'éclairement du disque apparent.
L'Union Astronomique Internationale publie régulièrement les paramètres qui permettent de définir la rotation des corps ainsi qu'un système de coordonnées pour situer le relief ou les structures de surface de ces corps.
Le pôle nord est, par définition, celui des deux pôles de l'axe de rotation qui se trouve au nord du plan invariant du système solaire (plan proche de l'écliptique). Les longitudes sont comptées à partir du méridien origine mais dans le sens opposé à la rotation. Il résulte de ceci que, pour un observateur lointain, la longitude planétographique du centre du disque apparent augmente toujours avec le temps, quel que soit le sens de rotation de l'astre. Afin de respecter une tradition historique et de pouvoir continuer à utiliser des cartes anciennes, on admet en général des exceptions à cette règle quand il s'agit de la Terre, du Soleil et de la Lune dont les rotations sont directes.
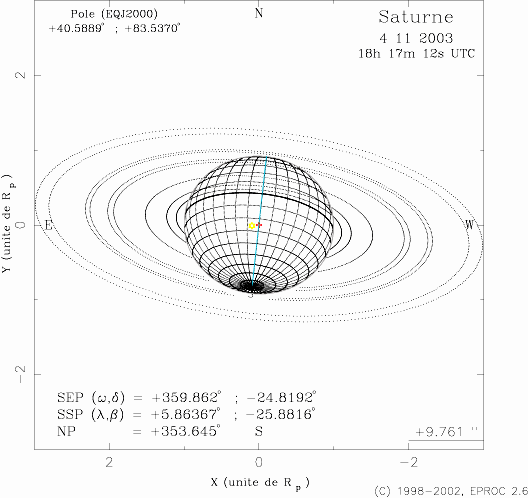
Aspect de la planète Saturne et de ses anneaux le 4 novembre 2003 à 18h17m12s UTC en unités "rayon de Saturne"
SEP = lonitude et latitude planétocentriques de la Terre en degrés
SSP = longitude et latitude planétocentriques du Soleil en degrés
NP = angle de position du pôle Nord de la planète par rapport au pôle Nord céleste en degré
Crédit :
I.M.C.C.E.
Le repérage des éphémérides de position
Les systèmes de référence
La connaissance des positions et des mouvements des astres nécessite d'avoir des notions précises des systèmes de référence de coordonnées spatiales et temporelles où l'on va situer les positions décrites par les éphémérides. Nous avons vu précédemment que l'argument temps des éphémérides ne pouvait être pris dans n'importe quelle échelle de temps. De même, nous allons voir que les coordonnées spatiales à utiliser doivent être rattachées à un système de référence grâce à un repère de référence.
On distingue les systèmes de référence célestes et terrestres.
Les systèmes de référence célestes sont soit dynamiques (basés sur l'étude dynamique des mouvements des corps du système solaire) soit cinématiques (basés sur l'étude statistique des mouvements des corps lointains tels que les étoiles, les galaxies et les quasars). Les systèmes de référence célestes dynamiques, tout d'abord construits dans la mécanique newtonienne, le sont aujourd'hui dans la mécanique relativiste qui lie l'argument temps aux variables spatiales. Pour les besoins des éphémérides actuelles, les définitions que nous avons données pour l'argument temps des éphémérides sont suffisantes. Pour rattacher les positions des corps célestes à un observateur situé sur la Terre, on a besoin de définir également un système de référence terrestre.
Les systèmes de référence terrestres nécessitent la connaissance d'un modèle de Terre, de sa forme et de ses déformations au cours du temps. La détermination d'une position topocentrique nécessite de disposer d'un tel système pour connaître la position du lieu en question par rapport aux positions que l'on a dans le système céleste. Les éphémérides étant en général géocentriques, les positions des corps célestes doivent être définies d'abord dans un système de référence céleste.
Les repères de référence célestes
Un système de référence est un concept théorique et la construction d'éphémérides nécessite la connaissance d'un repère de référence qui est la matérialisation concrète d'un système de référence. Un repère de référence céleste sera donc associé à des théories dynamiques, à des constantes et à des catalogues d'étoiles.
Un repère de référence se définit par un plan de référence et par une direction privilégiée. Pour les éphémérides publiées actuellement, le plan de référence est l'équateur de la Terre (repère équatorial) ou l'écliptique, plan de l'orbite de la Terre autour du Soleil (repère écliptique). La direction de référence est celle de l'équinoxe, nœud ascendant de l'écliptique sur l'équateur, intersection des deux plans. Ces plans et cette direction sont liés à la Terre et nous allons définir différents repères de référence selon les théories et les constantes utilisées pour les construire, puis, pour chaque repère ainsi construit, nous allons fixer les plans et la direction de référence pour obtenir un repère parfaitement défini.
Les repères cinématiques liés aux étoiles
Ces repères sont définis par les positions et les mouvements propres des étoiles. Citons les catalogues FK4 et FK5 qui utilisent 1535 étoiles. Des repères utilisant par exemple les étoiles du catalogue Hipparcos et des radiosources très lointaines sont utilisés comme catalogue pour l’astronométrie. Ils seront supplantés par le catalogue issu de la mission GAIA en cours de construction. Deux versions de ce catalogue existent déjà (2018).
Les repères dynamiques liés aux corps du système solaire
Les modèles dynamiques des corps du système solaire ajustés sur les observations radar ou laser sont indépendantes des étoiles des catalogues et définissent un plan et une direction de référence. Associés à une théorie de la précession - nutation, ils définissent un repère. Citons le repère lié aux intégrations numériques « DE430/DE431 du Jet Propulsion Laboratory ou encore INPOP de l’IMCCE et celui lié aux théories analytiques ELP2000/VSOP87 de la Lune et des planètes du Bureau des longitudes.
Les systèmes de coordonnées
Une fois défini un repère de référence, il faut choisir les coordonnées à utiliser pour fournir des positions dans les éphémérides.
A un repère de référence donné, on associe une théorie de la précession - nutation et on définit :
- les positions dans le repère moyen (les plans fondamentaux sont ici des plans moyens, c'est-à-dire affectés de la seule précession). Une date doit être donnée pour fixer le repère mais cette date est conventionnelle (par exemple 1950 pour le repère FK4 et 2000 pour le FK5) ;
- les positions dans le repère vrai (les plans fondamentaux sont affectés de la précession et de la nutation). La date du repère est celle à laquelle on donne les positions : le repère n'est pas fixe. C'est le seul repère accessible directement par un observateur terrestre.
Dans le repère ainsi défini, les coordonnées peuvent être :
- géométriques : ce sont les positions occupées réellement par le corps considéré à l'instant donné, sans tenir compte de la vitesse de la lumière ;
- apparentes : ce sont les positions vues par un observateur placé au centre du repère. Elles sont rapportées à un repère vrai de la date. On tient compte de la vitesse de la lumière et de l'aberration annuelle.
- astrométriques ou astrographiques : ce sont des coordonnées directement comparables aux catalogues d'étoiles. Elles se déduisent des coordonnées apparentes par la transformation de précession - nutation pour se ramener à un repère fixe (de la date du catalogue d'étoiles) et par la suppression de l'aberration annuelle. Le temps de lumière est toujours pris en compte.
Les coordonnées sont en général données sous forme sphériques, c'est-à-dire sous forme d'ascension droite et de déclinaison dans le repère équatorial ou sous forme de longitude et de latitude dans le repère écliptique. Elles peuvent être données sous forme d'angle horaire à la place de l'ascension droite pour un instant donné dans un repère local. Enfin, toujours dans un repère local, on peut donner l'azimut et la hauteur d'un astre à un instant donné. On consultera le cours sur la sphère céleste et les repères en astronomie pour plus de détails sur ces coordonnées.
Les coordonnées géométriques sont fournies sous forme cartésiennes X, Y, Z dans un repère équatorial, l'axe X étant dirigé vers le point vernal et l'axe Z vers le pôle Nord.
Enfin des coordonnées tangentielles ou différentielles peuvent être données pour des corps proches relativement l'un à l'autre sur un plan tangent à la sphère céleste.
Représentation des éphémérides
Les éphémérides sous forme de tables
La plus ancienne forme sous laquelle les éphémérides fournissent les positions des astres est une table de positions dont l'intervalle (une heure, un jour, un mois, ...) dépend de la vitesse de variation des valeurs de ces positions. Plus cette variation est rapide, plus petit doit être l'intervalle de temps séparant deux données successives. La simple lecture d'une table, accompagnée d'une interpolation à vue, suffit pour fournir une position permettant de repérer l'astre dans le ciel. Cependant, si l'on souhaite une précision plus grande, il faut effectuer une interpolation qui n'est plus linéaire, ce qui demande des calculs plus complexes à partir des valeurs publiées si celles-ci le permettent. Pour une précision plus grande, il faut diminuer l'intervalle entre deux positions et donc augmenter le volume de données publiées. L'Astronomical Almanac et le Guide des données astronomiques encore aujourd'hui, et la Connaissance des Temps jusqu'en 1979, contiennent des éphémérides sous forme de telles tables.
Citons le cas de la Lune : pour une précision de 0.01 seconde de degré, l'intervalle entre deux positions doit être de 3 heures ce qui conduit à la publication de 2920 valeurs annuellement par coordonnée. Citons aussi le cas des satellites galiléens de Jupiter qui ont un mouvement extrêmement rapide autour de Jupiter. Une éphéméride tabulée aurait nécessité un pas toutes les 20 minutes soit près de 30 000 valeurs pour une année! Cela conduit à un volume de données trop important pour être publié tel quel dans une éphéméride imprimée. D'autres solutions doivent être trouvées.
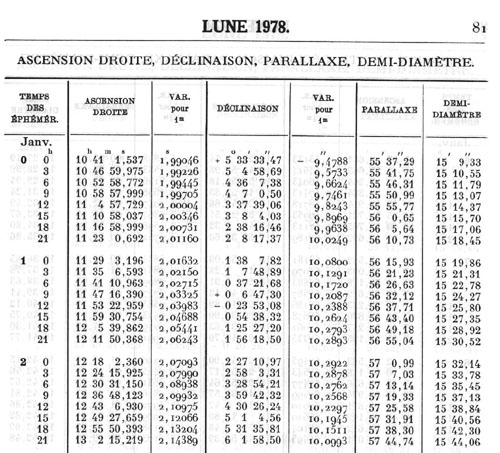
Un extrait de la Connaissance des Temps pour 1978 : l'ascension droite et la déclinaison de la Lune sont données de 3h en 3h avec la variation pour une minute. Le nombre de données à publier et les calculs d'interpolation à réaliser pour une précision correcte sont importants.
Crédit :
Bureau des Longitudes
En savoir plus: l'interpolation des éphémérides
 En savoir plus
En savoir plus
Une éphéméride est une table qui fournit, pour des dates particuières en principe équidistantes, les valeurs d'une ou de plusieurs fonctions qui décrivent l'évolution des positions des astres concernés, ou d'autres grandeurs relatives à ces astres. On appelle interpolation la technique de calcul qui permet d'évaluer les valeurs de ces fonctions pour des dates intermédiaires autres que celles qui figurent dans l'éphéméride.
Le cas le plus simple est celui où la fonction considérée varie assez lentement, ou est donnée avec assez peu de précision pour qu'aucun calcul ne soit nécessaire. On se contente alors d'une interpolation à vue (par exemple, magnitude de la planète Jupiter : aucun calcul n'est nécessaire, quand on examine l'éphéméride du chapitre 5, pour estimer que sa valeur est -1,8 le 2 juillet 2002).
Plus souvent, on devra employer l'interpolation linéaire et procéder comme suit. Soit :
t, l'instant pour lequel on veut calculer le fonction f ;
t1, l'instant immédiatement inférieur ou égal à t et figurant dans l'éphéméride, la valeur correspondante de f étant f1 ;
t2, l'instant immédiatement supérieur à t et figurant dans l'éphéméride, la valeur correspondante de f étant f2.
Alors, on calculera f par la formule :
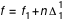
où
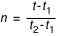 et
et 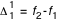
s'appellent respectivement facteur d'interpolation et différence première.
Dans certains cas, l'interpolation linéaire fournit un résultat trop imprécis. Pour s'en rendre compte, on forme le tableau suivant :

où t0, t1, t2, t3, etc sont des instants figurant dans l'éphéméride, et f0, f1, f2, f3, etc les valeurs correspondantes de la fonction f données par cette éphéméride. Les quantités :
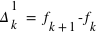
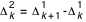 {k=0,1,2,...}
{k=0,1,2,...}
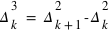
s'appellent respectivement différences premières, différences secondes, différences troisièmes, etc. L'interpolation linéaire est suffisante si les différences secondes sont inférieures à 4 unités du dernier ordre envisagé. Sinon (et à condition que les différences troisièmes n'excèdent pas 62 unités du dernier ordre envisagé, ce qui sera toujours le cas dans cet ouvrage), on emploie la formule de Bessel :
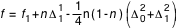
où n est le même facteur d'interpolation que plus haut, et, compte tenu des expressions ci-dessus :
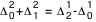
Les éphémérides sous forme graphique
Comme nous l'avons vu, les corps rapides comme les satellites de Jupiter ne peuvent avoir des éphémérides précises publiées annuellement. Une première solution consiste alors à offrir au lecteur une représentation graphique dont la lecture conduit à une précision de quelques dizaines de secondes de degré, précision bien faible mais suffisante pour identifier les corps lors d'une observation. On trouvera ci-dessous les configurations des satellites de Jupiter publiées par la Connaissance des temps. A gauche pour un mois de l'année 1808 et à droite pour 2000.

Crédit :
Bureau des Longitudes
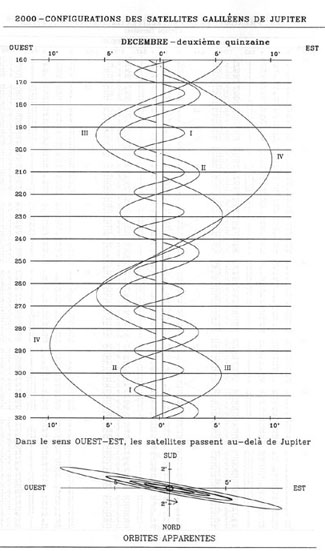
Crédit :
Bureau des Longitudes
Détermination de la configuration des satellites de Jupiter à une date donnée
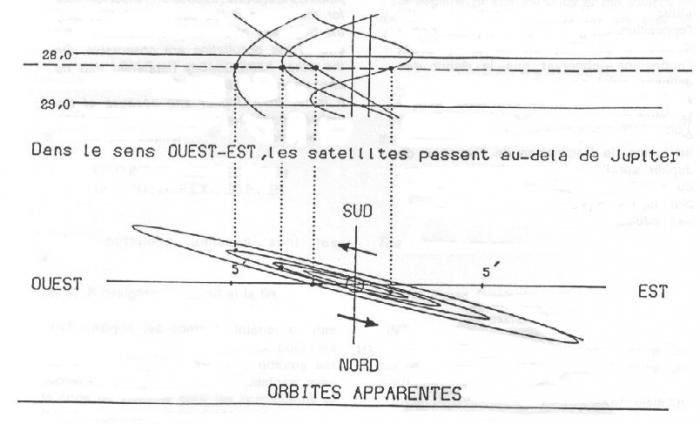
Crédit :
Bureau des Longitudes/Jean-Eudes ARLOT
Approximation d'une fonction par un polynôme
L'usage très répandu aujourd'hui des calculatrices de poche et des micro-ordinateurs permet d'utiliser une formulation plus complexe pour les éphémérides et on va chercher plutôt à conserver une précision de représentation optimale sur la période de temps couverte par l'éphéméride. Ainsi, au lieu d'évaluer une fonction f(t) sous la forme d'un tableau de valeurs calculées à des intervalles rapprochés du temps, on va établir des fonctions d'approximation de f(t) valables sur de grands intervalles de temps, en minimisant les erreurs et le volume global des données.
L'éphéméride veut donc représenter une fonction f(t) constituée, soit par le résultat d'une intégration numérique, soit par une fonction analytique du temps qui traduit le mouvement d'un corps ou l'évolution temporelle d'un phénomène. Or, on sait que toute fonction peut être approchée sur un intervalle de temps donné par un polynôme dont le degré et le nombre de termes sont d'autant plus élevés que l'intervalle de temps est grand. Une telle approximation n'est pas optimisée et le volume de données à publier est important mais l'utilisation d'une telle éphéméride est très simple puisqu'il suffit de substituer le temps dans les polynômes ainsi construits. D'autres représentations sont cependant bien meilleures.
En savoir plus: approximation de Tchebychev (1)
 En savoir plus
En savoir plus
Les fonctions que nous voulons approcher sont toujours définies pour toutes les valeurs de la variable temps. L'approximation lagrangienne par des polynômes consiste à faire passer, pour un intervalle donné, un polynôme de degré n par n+1 valeurs, alors qu'il serait préférable de tenir compte de toutes les valeurs de la fonction sur cet intervalle. L'approximation de Tchebychev s'impose pour cela, car elle est celle de plus bas degré dont l'erreur ne dépasse pas une valeur donnée a priori, et son erreur est régulièrement distribuée sur l'intervalle considéré.
La fonction d'approximation va se présenter comme une suite de développements en polynômes de Tchebychev sur une succession d'intervalles de temps. Ainsi le volume de données est réduit et le calcul des positions est rapide. Cette représentation est donc bien adaptée aux besoins des astronomes (amateurs, professionnels, théoriciens, astrométristes, ...).
Les éphémérides Tchebychev se présentent sous la forme d'une suite de coefficients a0, a1, ...an pour une coordonnée donnée sur un intervalle [t1, t2]. L'utilisation de ces éphémérides se fait de la manière suivante. Le calcul de la valeur de la coordonnée à l'instant t de l'intervalle [t1, t2] se fait en effectuant le changement de variable :
x=-1+{2(t-t1)}/{t2-t1}, donc x appartient à l'intervalle [-1, +1]
Les polynômes de Tchebychev de première espèce Tn(x) sont donnés par la relation :
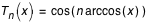
On peut aussi les calculer à l'aide de la relation de récurrence :
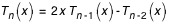 avec
avec 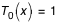 et
et 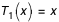
La coordonnée est alors égale à :
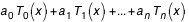
Dans la majorité des éphémérides -Soleil, Lune, planètes-, on a choisi des polynômes de Tchebychev pour la réalisation des éphémérides. Voyons maintenant comment calculer une position à partir de cette représentation.
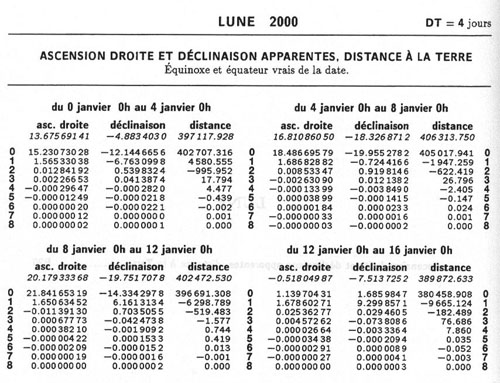
Crédit :
I.M.C.C.E.
Ci-contre, un extrait de la Connaissance des Temps pour l'année 2000 : l'ascension droite et la déclinaison sont fournies sous forme de coefficients : il faut programmer un petit formulaire simple pour calculer les valeurs pour tout instant de l'intervalle de validité. Les données à publier sont peu importantes et la précision des valeurs obtenues est la meilleure.
En savoir plus: approximation de Tchébychev (2)
 En savoir plus
En savoir plus
Soleil, Lune, Planètes
Soit t une date julienne appartenant à l'intervalle de temps t0, t0 + DT et y une coordonnée d'un astre. On calcule 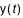 par la formule :
par la formule :
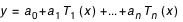
Où
- x est un paramètre compris entre -1 et +1 qui se déduit de t par la relation :
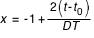
- a0, a1, ..., an sont les coefficients numériques publiés dans la Connaissance des Temps, valables pour l'intervalle de temps t0, t0 + DT contenant t :
- T1(x), ..., Tn(x) sont des polynômes de Tchebychev, en x, que l'on calcule :
- soit par la relation :
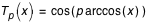 ;
; - soit par la relation de récurrence :
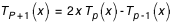 Avec :
Avec : 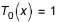 ;
; 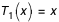
Caractéristiques générales
Les éphémérides de l'année sont publiées corps par corps. Pour chaque corps, on compte un certain nombre de variables qui pour des intervalles de temps donnés, sont représentées par des tableaux donnant les coefficients de leurs développements en polynômes de Tchebychev ou sous forme de fonctions mixtes.
En haut de chaque page, on trouve :
- le nom du corps concerné suivi de l'année de l'éphéméride ;
- le type des variables représentées ;
- éventuellement, les caractéristiques du système de coordonnées.
En bas de chaque page, on trouve les unités utilisées.
Les coefficients d'un tableau sont publiés en colonne. Pour chaque tableau, on précise :
- le nom de la variable représentée ;
- les dates de début et de fin de l'intervalle de temps correspondant au domaine de validité du tableau.
- la longueur des intervalles de temps DT (en jours) figure en haut de chaque page ;
- les coefficients sont notés 0, 1, ..., p,... n;
- la valeur de contrôle du tableau, imprimée en italique, figure en tête de chaque tableau. C'est la valeur y(t0) de la variable y représentée par le tableau, pour t0 début de l'intervalle de temps t0, t0 + DT. Elle est égale à :
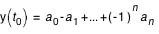
La valeur de contrôle permet de vérifier que les coefficients ont été correctement entrés en mémoire sur une calculette ou un calculateur. De plus, l'ensemble des valeurs de contrôle des tableaux d'une même variable donne une idée de l'évolution de cette variable au cours de l'année.
Calcul d'une coordonnée
Pour calculer la valeur d'une coordonnée d'un astre pour une date t exprimée en UTC, on commence par :
- effectuer, sur t, une correction déduite de la table 2 afin de se ramener à l'argument des éphémérides (identifié à TT) :
- chercher, parmi les tableaux représentant la coordonnée, celui qui correspond à l'intervalle de temps t0, t0 + DT dans lequel se trouve t. Il faut insister sur le fait que la représentation, qu'elle soit en polynômes de Tchebychev ou sous forme de fonctions mixtes, n'est pas valable en dehors de l'intervalle t0, t0 + DT.
Le calcul se poursuit de la manière suivante :
Soleil, Lune, Planètes
- On calcule x par la formule (2).
- A partir des n + 1 coefficients du tableau a0, a1, ..., ap, ..., an (notés 0, 1,... p, ..., n), on calcule la coordonnée y(t) par la formule (1).
- Les polynômes de Tchebychev tp(x) se calculent soit par la formule (3), soit par la relation de récurrence (4). Notons que, si on n'utilise que les p + 1 (p < n) premiers coefficients du développement en polynômes de Tchebychev, on commet, sur la représentation de y, une erreur au plus égale à la somme des valeurs absolues des n - p coefficients négligés.
- Pour avoir le temps de passage du Soleil au méridien origine en un jour donné, numéroté j dans le mois, on applique la même méthode en prenant t = j + 0,5.
En savoir plus: approximation de Tchébychev (3) exemple de calcul
 En savoir plus
En savoir plus
Exemple 1. Calculer le rayon vecteur héliocentrique de Mars le 5 Novembre 2003 à 16h 51m 42s UTC.
On effectue d'abord une correction pour se ramener à l'argument des éphémérides. Pour 2003, la valeur de TT - UTC n'est pas encore connue, mais on peut la prendre égale à 65 s. La date t est donc le 5 novembre 2003 à 16h 52m 47s argument des éphémérides.
On utilise les coefficients de la page B36 valables du 0 juillet 0h au 33 décembre 0h. Le calendrier des pages B148 et B149 donne les numéros JDA des jours de l'année correspondant au 0 juillet (JDA = 181) et au 5 novembre (JDA = 309). On a :
DT = 186 ;
t - t0 = 309 - 181 + 16h 52m 47s = 128.703 321 759 jours
On en déduit par la formule (2) :
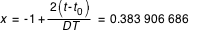
On peut calculer les polynômes de Tchebychev par l'un des deux algorithmes suivants :
Algorithme 1
Les polynômes de Tchebychev 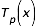 sont calculés par la relation (3) :
sont calculés par la relation (3) :
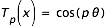 où
où 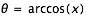
On a : θ = 67°.424 117 27. On en déduit :
T1(x)= cos (θ) = x = 0.383 906 686
T2(x)= cos 2(θ) = -0.705 231 314
T4(x)= cos 4(θ) = -0.005 297 589
T6(x)= cos 6(θ) = 0.712 703 365
T8(x)= cos 8(θ) = -0.999 943 871
Algorithme 2
Les polynômes 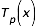 sont calculés par la relation de récurrence (4) :
sont calculés par la relation de récurrence (4) :
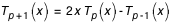
avec : 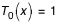 ;
; 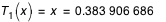
On en déduit :
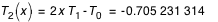 ,
,
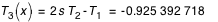 , etc
, etc
Les polynômes de Tchebychev étant déterminés, le rayon vecteur R de Mars se déduit de la formule (1) :
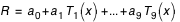 ,
,
Où les coefficients de a0, a1, ..., a9 sont ceux du tableau de la page B36 valables du 0 juillet 0h au 33 décembre 0h. On a donc :
R = 1.415 514 22 + 0.035 889 20 T1 + ... + 0.000 000 04 T9,
Soit finalement :
R = 1.412 255 01 ua.
Table des coefficients des polynômes de Tchébychev
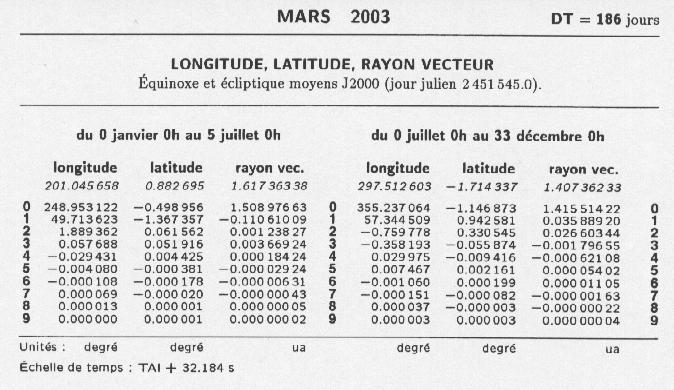
Crédit :
I.M.C.C.E.
En savoir plus: approximation par des fonctions mixtes (1)
 En savoir plus
En savoir plus
Comme nous l'avons vu, l'approximation polynomiale n'est pas la seule possible pour représenter une éphéméride. L'introduction des fonctions mixtes, permet de prendre en compte le caractère quasi-périodique des fonctions qui apparaissent dans les éphémérides. En effet, une fonction quasi-périodique à variations faibles sur un intervalle donné peut être approchée par un développement en polynômes de degré n peu élevé mais on n'a pas utilisé le fait que la fonction soit quasi-périodique sur l'intervalle considéré, ce qui est le cas du mouvement des corps du système solaire.
Voyons par un exemple comment en tirer parti.
Soit la fonction paire
f(x) = cos x + cos 2x
Elle est beaucoup mieux représentée avec la base de fonctions
1, cos x, cos 2x, cos 3x,... qu'avec la suite de polynômes
1, x2, x4, x6,... , ou toute autre base de polynômes pairs.
Si une éphéméride n'est jamais aussi simple dans la réalité, on peut toujours l'approcher par une combinaison de fonctions périodiques dont les périodes proviennent de la nature physique du phénomène (par exemple la périodede révolution d'un corps céleste), et de termes séculaires (polynômes du temps) qui témoignent du caractère non rigoureusement périodique du phénomène ou du mouvement décrit.
Le mode de représentation à l'aide des fonctions mixtes est très bien adapté à la représentation des mouvements des satellites naturels des planètes et des corps à période courte qui s'écartent peu, sur quelques périodes, d'un mouvement périodique, avec des variations d'amplitude et de fréquence lente par rapport à la période principale du corps et de ses multiples entiers.
Dans la Connaissance des Temps on trouve en particulier l'expression des coordonnées différentielles des satellites naturels des planètes sur des intervalles de temps couvrant une à quelques révolutions, avec des formules faciles à mettre en œuvre directement par l'utilisateur et qui se présentent ainsi :
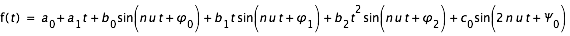 .
.
où 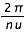 est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les φj et Ψj sont les phases (j = 0, 1, 2). Cette formule découle du choix de la base. Les termes mixtes sont de la forme : A tksin(p nu t + Ψ) (k et p entiers A : amplitude ; Ψ : phase). Sur un intervalle de temps donné les valeurs maximales de k et p sont ajustées en fonction de la précision recherchée. Si l'intervalle de représentation est élargi, il faudra enrichir la base de termes mixtes en puissance du temps et en multiples de la fréquence de base. Mais si l'intervalle de temps se rétrécit, il faut également modifier la base sous peine de perdre de la précision (ce n'est pas le cas avec la représentation à l'aide de polynômes dont la précision augmente quand l'intervalle diminue.
est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les φj et Ψj sont les phases (j = 0, 1, 2). Cette formule découle du choix de la base. Les termes mixtes sont de la forme : A tksin(p nu t + Ψ) (k et p entiers A : amplitude ; Ψ : phase). Sur un intervalle de temps donné les valeurs maximales de k et p sont ajustées en fonction de la précision recherchée. Si l'intervalle de représentation est élargi, il faudra enrichir la base de termes mixtes en puissance du temps et en multiples de la fréquence de base. Mais si l'intervalle de temps se rétrécit, il faut également modifier la base sous peine de perdre de la précision (ce n'est pas le cas avec la représentation à l'aide de polynômes dont la précision augmente quand l'intervalle diminue.
Voyons maintenant l'application des fonctions mixtes pour la représentation du mouvement d'un satellite de planète en révolution rapide.
En savoir plus: approximation par des fonctions mixtes (2)
 En savoir plus
En savoir plus
Satellites
Soit t une date julienne appartenant à l'intervalle de temps t0, t0 + DT. On calcule les coodonnées X et Y d'un satellite pour la date t par la formule (Chapront et Vu, 1984) :
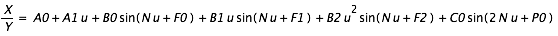 (5),
(5),
où :
- u = t - t0 ; u est compté en jours ;
- A0, A1, B0, F0, B1, F1, B2, F2, C0, P0 sont les coefficients numériques publiés dans la Connaissance des temps, valables pour l'intervalle de temps t0, t0 + DT contenant t ;
- N est la fréquence associée au satellite considéré. Elle est proche de celle du satellite lui-même, sauf dans le cas d'Hypérion pour lequel on prend une fréquence proche de celle de Titan du fait de l'existence d'un très gros terme perturbateur de fréquence plus grande que celle du satellite lui-même.
Caractéristiques générales
Les éphémérides de l'année sont publiées corps par corps. Pour chaque corps, on compte un certain nombre de variables qui, pour des intervalles de temps donnés, sont représentées par des tableaux donnant les coefficients de leurs développements en polynômes de Tchebychev ou sous formes de fonctions mixtes.
En haut de chaque page, on trouve :
- le nom du corps concerné suivi de l'année de l'éphéméride ;
- le type des variables représentées ;
- éventuellement, les caractéristiques du système de coordonnées.
En bas de chaque page, on trouve les unités utilisées.
Les coefficients d'un tableau sont publiés en colonne. Pour chaque tableau, on précise :
- le nom de la variable représentée ;
- les dates de début et de fin de l'intervalle de temps correspondant au domaine de validité du tableau.
Satellites
- la valeur de la fréquence N (en radians par jour) associée au satellite figure en haut de chaque page ;
- les coefficients sont notés A0, A1, B0, B1, F0, F1, B2, F2, C0, P0. Pour quelques satellites, certains coefficients ne sont pas donnés car ils sont nuls.
- A0, B0, C0 sont exprimés en secondes de degré par jour ;
- A1, B1 sont exprimés en secondes de degré par jour ;
- B2 est exprimé en secondes de degré par (jour)2 ;
- F0, F1, F2, P0 sont exprimés en radians ;
- dans la formule (5) u est compté en jours à partir du début de l'intervalle (époque t0).
Calcul d'une coordonnée
Pour calculer la valeur d'une coordonnée d'un astre pour une date t exprimée en UTC, on commence par :
- effectuer, sur t, une correction déduite de la table 2 afin de se ramener à l'argument des éphémérides (identifié à TT) ;
- chercher, parmi les tableaux représentant la coordonnée, celui qui correspond à l'intervalle de temps t0, t0 + DT dans lequel se trouve t. Il faut insister sur le fait que la représentation, qu'elle soit en polynômes de Tchebychev ou sous forme de fonctions mixtes, n'est pas valable en dehors de l'intervalle t0, t0 + DT.
Le calcul se poursuit de la manière suivante :
On applique la formule (5) avec 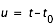 (u est compté en jours).
(u est compté en jours).
En savoir plus: Exemple de calcul
 En savoir plus
En savoir plus
Exemple 2. Calculer les coordonnées tangentielles de Téthys (troisième satellite de Saturne) par rapport à la planète, le 4 janvier 2003 à 23h 29m 57s UTC.
On effectue la même correction de 65s que dans l'exemple 1 pour se ramener à l'argument des éphémérides. La date t est donc le 4 janvier 2003 à 23h 31m 02s argument des éphémérides.
On utilise les coefficients de la page B120 valables du 0 janvier 0h au 16 janvier 0h. On a, pour X :
A0 = -0.001 000, A1 = 0.0
B0 = 50.188 200, F0 = 2.518 466, etc.
et, pour Y :
A0 = 0.002 100, A1 = 0.000 010,
B0 = 23.773 900, F0 = 1.092 443, etc.
On applique ensuite la formule (5) :
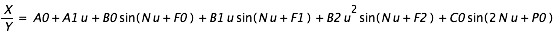 ,
,
où : N = 3.3280 radians/jours ;
u est le nombre de jours écoulés entre le 0 janvier à 0h et le 4 janvier à 23h 31m 02s, soit 4.979 884 jours. On obtient finalement :
X = 12".387,
Y = -21".897.
Table de coefficients de fonctions mixtes

Crédit :
I.M.C.C.E.
La précision des éphémérides
Lorsque l'on utilise une éphéméride pour calculer la position d'un corps du système solaire, on est amené à se poser la question : quelle est la précision de la quantité calculée ? Où se trouvera le corps observé par rapport à la position calculée ? On veut donc connaître la précision de l'éphéméride ou plutôt son exactitude. La précision des éphémérides est la résultante de trois types de précisions différentes :
- la précision interne de la théorie dynamique utilisée pour modéliser le mouvement et qui dépend de l'importance des termes des séries négligées et qui peut être évaluée à l'aide d'une comparaison à une intégration numérique (la précision interne est en général la meilleure) ;
- la précision externe de la théorie utilisée qui dépend de la précision des observations utilisées pour l'ajustement des constantes d'intégration de cette théorie et aussi de la répartition des observations au cours du temps (c'est la précision externe qui limite la précision globale des éphémérides) ;
- la précision de la représentation que l'on choisit en ajustant le nombre de coefficients et la longueur des intervalles de validité ou en interpolant une table (cette précision est la seule que l'on puisse choisir, elle ne doit pas dégrader la précision globale).
Aujourd'hui, la précision avec laquelle on peut positionner une planète ou un satellite de planète est la suivante :
| Soleil/Terre | 0,3" | 220 km |
| Mercure | 0,9" | 440 km |
| Vénus | 0,3" | 70 km |
| Lune | 0,008" | 15 m |
| Mars | 0,4" | 60 km |
| Jupiter | 0,5" | 1500 km |
| Satellites galiléens de Jupiter | 0,1" | 300 km |
| Saturne | 0,9" | 5400 km |
| Titan | 0,2" | 1200 km |
| Uranus | 0,5" | 6550 km |
| Neptune | 1,0" | 20 000 km |
| Pluton | 1,0" | 20 000 km |
A noter que pour les besoins de l'exploration spatiale, on est amené à construire des éphémérides de dernière minute plus précises mais se dégradant très rapidement dans le temps.
Les phénomènes astronomiques
Qu'est-ce qu'un phénomène astronomique ?
On appelle "phénomène astronomique" une configuration particulière des astres que l'on peut prévoir. Ce phénomène peut être perceptible sans instrument d'observation (éclipse de Lune ou de Soleil, lever d'un astre, ...). Les éphémérides vont donc prévoir ces phénomènes. Dans certains cas (éclipses de Soleil, lever et coucher d'un astre), la visibilité du phénomène est locale et les paramètres publiés dans l'éphéméride seront généraux. Il faudra prévoir des tables, des formules avec coefficients ou des graphiques pour savoir ce qui se passe dans un lieu précis.
Les principaux phénomènes donnés sont :
- les levers et couchers des astres
- les éclipses de Soleil et de Lune
- les passages de Mercure et Vénus devant le Soleil
- les phénomènes des satellites de Jupiter et de Saturne.
On se reportera au cours sur les éclipses pour le détail des calculs et des prédictions de ces phénomènes.
Lever et coucher d'un astre en un lieu donné
Lever et coucher des astres
Pour calculer l'instant du lever ou du coucher d'un astre dont on suppose connues les coordonnées équatoriales approchées α et δ au moment du phénomène considéré, on calcule d'abord l'angle horaire H au moment du lever ou du coucher par la formule :
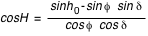 où
où
φ est la latitude du lieu et h0 un angle petit qui sera défini plus loin. Le temps sidéral approché du lever est alors :
(2a) 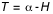 ;
;
et celui du coucher,
(2b) 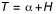 .
.
On calcule ensuite, à partir de T, l'instant du phénomène en temps universel comme on l'a expliqué dans les paragraphes précédents.
Si l'astre se déplace rapidement sur la sphère céleste (c'est le cas pour le Soleil, certaines planètes et surtout la Lune), on calcule pour l'instant trouvé des coordonnées α et δ plus exactes en interpolant les tables et l'on recalcule H puis T, par les formules (1) et (2), d'où l'instant du phénomène en UT. Pour la Lune, on est quelquefois amené à effectuer une itération supplémentaire.
Quant à h0, son expression générale est la suivante :
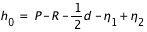 ,
,
P est la parallaxe. On la néglige pour tous les astres sauf pour la Lune pour laquelle P = 57'.
R est la réfraction à l'horizon. Les tables du présent volume utilisent la théorie de la réfraction de Radau qui conduit à R = 36'36", mais l'on pourra utiliser la valeur R = 34' adoptée dans les Ephémérides Nautiques publiées par le Bureau des longitudes et dans d'autres publications étrangères.
(1/2) d est le demi-diamètre apparent de l'astre. On l'introduit dans la formule quand on calcule le lever et le coucher du bord supérieur du Soleil et de la Lune et non pas le lever et le coucher du centre de l'astre. On prend, aussi bien pour le Soleil que pour la Lune, (1/2) d = 16'.
Si l'observateur est à une altitude A au-dessus du niveau de la mer, on introduit dans 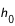 l'angle
l'angle 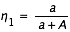 , où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
, où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
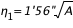 ,
,
A étant exprimé en mètres.
Si l'on cherche le lever ou le coucher d'un astre en un lieu dont l'horizon est limité par des collines ou des montagnes d'altitude 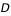 situées à la distance
situées à la distance 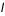 de l'observateur, on ajoutera à
de l'observateur, on ajoutera à 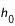 l'angle
l'angle 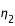 tel que :
tel que :
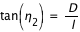 .
.
On ne cherchera pas à obtenir les instants du lever ou du coucher des astres avec une précision supérieure à une minute, la valeur exacte de la réfraction à l'horizon au moment du phénomène étant trop mal connue.
Calcul d'un coucher ou d'un lever d'un astre
Coucher à Bordeaux de l'étoile Sirius le 20 Avril 2002.
Les coordonnées moyennes de l'étoile pour 2002 sont (chapitre 10, "Positions d'étoiles") :
α = 6h 45m 15s ; δ= - 16°43'11".
En faisant les corrections de précession pour le 20 avril (données à la fin de ce chapitre), on trouve :
α = 6h 45m 16s, δ = 16°43'12".
Ici P = 0, (1/2) d = 0, η1 = 0, η2 = 0 ;
d'où :
h0 = -R = -34'
Les coordonnées de Bordeaux sont :
λ = + 2m 7s φ = + 44°50'7".
On déduit de la formule (1) :
cos H = 0,28411 d'où H = 73,494° = 4h 53m 59s.
Et le temps sidéral du coucher est :
T = α + H = 11h 39m 15s.
Le temps sidéral de Greenwich est donc :
T1 = T + λ = 11h 41m 22s
Le temps sidéral de Greenwich à 0h le 20 avril 2002 est T0 = 13h 51m 38s (chapitre "Positions du Soleil et de la Lune").
d'où :
Tt = T1 - T0 = 21h 49m 44s.
En convertissant cet intervalle de temps sidéral en un intervalle de temps moyen, on trouve que Sirius se couche à Bordeaux le 20 avril 2002 à :
t = 21h 46m 9s (UT)
Les phénomènes des satellites de Jupiter
Les satellites galiléens présentent des phénomènes particuliers dus aux positions que prennent le Soleil, Jupiter et la Terre : les éclipses (lorsqu'un satellite passe dans l'ombre de Jupiter) ; les occultations (lorsqu'un satellite passe derrière Jupiter par rapport à la Terre) ; les passages (lorsqu'un satellite passe devant Jupiter par rapport à la Terre) et les passages d'ombre (lorsque l'ombre d'un satellite passe sur le disque de Jupiter). Les phénomènes les plus célèbres sont les éclipses car ils sont les plus faciles à observer : il s'agit de l'extinction ou de l'apparition d'un satellite isolé. Les autres phénomènes nécessitent l'observation simultanée de Jupiter ce qui dégrade beaucoup le rapport signal sur bruit.
Tous ces phénomènes ont été observés visuellement pendant des dizaines d'années et le grand nombre d'éclipses observées a constitué la base des premières éphémérides. Dès la fin du XIXème siècle, les techniques d'observation des éclipses se sont améliorées et les premières courbes photométriques ont permis d'améliorer la précision de la datation de ces phénomènes. Ensuite, les enregistreurs photoélectriques sont apparus mais, malgré le progrès qu'ils apportaient, ils ont été très peu utilisés : ils sont arrivés lorsque cessa l'intérêt des astronomes pour ce type de travaux et n'ont pas encore été repris pour des raisons de précision.
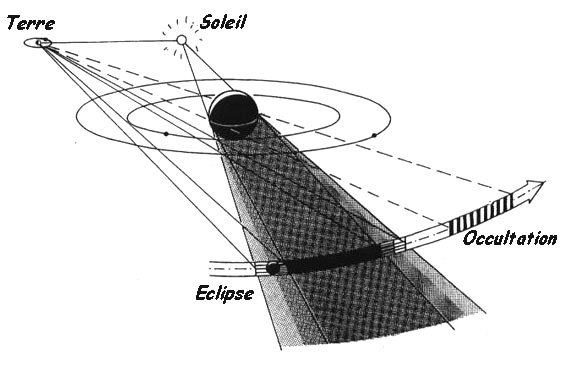
Les positions relatives de Jupiter, du Soleil et de la Terre pour que les satellites galiléens présentent des "phénomènes".
Crédit :
I.M.C.C.E./D.T. VU
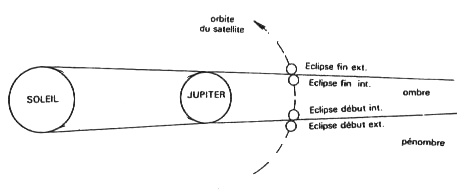
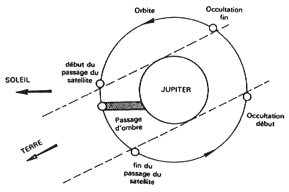
Configurations pour les différents types de phénomènes.
Crédit :
I.M.C.C.E./W. THUILLOT

Un passage d'ombres sur le disque de Jupiter.
Crédit :
Karkoshka et Murrell, NMSU
Où se procurer des éphémérides
Où trouver des éphémérides imprimées ?
Bien que la micro-informatique soit omniprésente pour les calculs astronomiques, les éphémérides imprimées sont encore abondamment diffusées auprès des astronomes professionnels ou amateurs. Pour quelle raison ? Tout d'abord, l'observateur a souvent besoin d'une confirmation ou d'une simple position approchée. Il est alors simple d'ouvrir un livre et de lire directement une valeur tabulée. On y trouve :
- les heures de lever et de coucher du Soleil et de la Lune (et aussi des planètes principales) ;
- les positions des corps du système solaire et des étoiles brillantes pour un observateur terrestre ;
- les éphémérides pour les observations physiques de ces corps.
Ces éphémérides sont en général de faible précision et des valeurs tabulées sont suffisantes.
Il faut également citer des éphémérides plus spécialisées dans lesquelles les positions des corps célestes sont données dans un but utilitaire : les éphémérides nautiques françaises et le Nautical Almanac anglo-américain sont publiées pour permettre aux marins de faire le point en mer et sont là pour suppléer une défaillance du système GPS. L'éphéméride imprimée garde ici toute son utilité.
Toutes les éphémérides imprimées ne fournissent pas toujours des données tabulées. Elles peuvent donner des représentations graphiques (pour les satellites de Jupiter) ou des coefficients pour polynômes, dans le cas des éphémérides de haute précision, qui nécessitent alors l'emploi d'une calculatrice de poche ou d'un micro ordinateur. C'est le cas de la Connaissance des temps depuis 1979 qui est alors utilisée pour la programmation manuelle des télescopes ou plus simplement pour les tests et les contrôles de programmation plus complexe.
On trouvera ci-dessous la liste des principales éphémérides imprimées publiées actuellement :
- par l'Institut de mécanique céleste et de calcul des éphémérides/Bureau des longitudes :
Guide des données astronomiques
Connaissance des Temps,
Ephémérides nautiques
- par la Société Astronomique de France,
Ephémérides astronomiques
- par le H.M. Nautical Almanac Office de l'ex-Royal Greenwich Observatory (Grande-Bretagne) aujourd'hui au Rutherford Appleton Laboratory et l'USNO (USA) :
Astronomical Ephemerides,
Nautical Almanac ;
- par l'Institut d'astronomie appliquée de Saint-Pétersbourg (Russie) :
Ephémérides des petites planètes ;
- par l'Astronomisches Rechen Institute d'Heidelberg (Allemagne) :
Apparent Places of Fundamental Stars.
Où trouver des éphémérides sur Internet ?
On trouve sur internet de nombreux sites fournissant des éphémérides. Là encore, la précision des positions calculées n'est fournie que sur les sites professionnels. Les données disponibles sont riches et abondantes. Les interfaces interactives sont en général faciles d'utilisation. Attention à l'interprétation des données obtenues !
- serveur de l'Institut de mécanique céleste et de calcul des éphémérides/Bureau des longitudes (Paris, France) http://www.imcce.fr/
- serveur du Jet Propulsion Laboratory (Pasadena, Californie, USA) : http://ssd.jpl.nasa.gov/
- serveur de l'U.S. Naval Observatory (Washington, D.C., USA) : http://aa.usno.navy.mil/
- serveur du H.M. Nautical Almanac Office de l'ex-Royal Greenwich Observatory (Grande-Bretagne) aujourd'hui au Rutherford Appleton Laboratory (Oxford, Grande-Bretagne) : http://www.ast.cam.ac.uk/
- serveur du Minor Planet Center (Cambridge, Massachussets, USA) : (éphémérides d'astéroïdes et de comètes exclusivement) http://minorplanetcenter.net/
Comment faire ses propres éphémérides ?
Fabriquer ses propres éphémérides pour quelques corps du système solaire est un exercice très formateur. Pour cela, il faut consulter les explications de base nécessaires, soit sur les sites Internet fournissant des éphémérides, qui fournissent aussi souvent des outils pour fabriquer soi-même des éphémérides (par exemple pour étendre l'intervalle de temps de validité des éphémérides), soit dans des ouvrages spécialisés. Citons :
- Introduction aux éphémérides astronomiques, Bureau des longitudes, Editions de Physique, avenue du Hoggar, ZA de Courtabœuf, BP 112, F-91944 Les Ulis Cedex, France (en français)
- Explanatory Supplement to the Astronomical Ephemeris, U.S. Naval Observatory/Rutherford Appleton Laboratory (en anglais)
 Introduction
Introduction


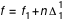
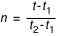 et
et 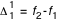

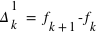
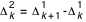 {k=0,1,2,...}
{k=0,1,2,...}
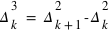
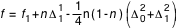
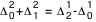



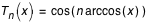
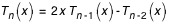 avec
avec 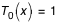 et
et 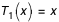
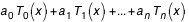

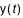 par la formule :
par la formule :
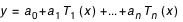
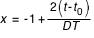
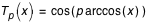 ;
; 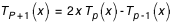 Avec :
Avec : 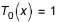 ;
; 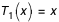
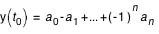
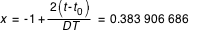
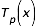 sont calculés par la relation (3) :
sont calculés par la relation (3) :
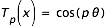 où
où 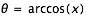
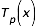 sont calculés par la relation de récurrence (4) :
sont calculés par la relation de récurrence (4) :
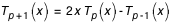
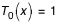 ;
; 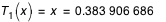
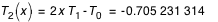 ,
,
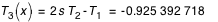 , etc
, etc
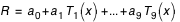 ,
,

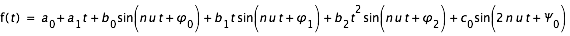 .
.
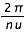 est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les
est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les 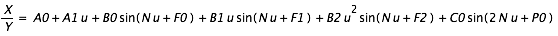 (5),
(5),
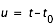 (u est compté en jours).
(u est compté en jours).
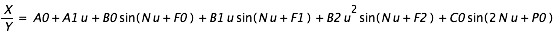 ,
,

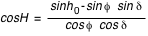 où
où
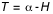 ;
;
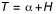 .
.
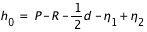 ,
,
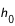 l'angle
l'angle 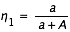 , où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
, où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
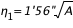 ,
,
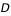 situées à la distance
situées à la distance 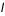 de l'observateur, on ajoutera à
de l'observateur, on ajoutera à 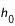 l'angle
l'angle 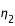 tel que :
tel que :
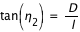 .
.



