On appelle "phénomène astronomique" une configuration particulière des astres que l'on peut prévoir. Ce phénomène peut être perceptible sans instrument d'observation (éclipse de Lune ou de Soleil, lever d'un astre, ...). Les éphémérides vont donc prévoir ces phénomènes. Dans certains cas (éclipses de Soleil, lever et coucher d'un astre), la visibilité du phénomène est locale et les paramètres publiés dans l'éphéméride seront généraux. Il faudra prévoir des tables, des formules avec coefficients ou des graphiques pour savoir ce qui se passe dans un lieu précis.
Les principaux phénomènes donnés sont :
- les levers et couchers des astres
- les éclipses de Soleil et de Lune
- les passages de Mercure et Vénus devant le Soleil
- les phénomènes des satellites de Jupiter et de Saturne.
On se reportera au cours sur les éclipses pour le détail des calculs et des prédictions de ces phénomènes.
Lever et coucher des astres
Pour calculer l'instant du lever ou du coucher d'un astre dont on suppose connues les coordonnées équatoriales approchées α et δ au moment du phénomène considéré, on calcule d'abord l'angle horaire H au moment du lever ou du coucher par la formule :
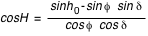 où
où
φ est la latitude du lieu et h0 un angle petit qui sera défini plus loin. Le temps sidéral approché du lever est alors :
(2a) 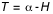 ;
;
et celui du coucher,
(2b) 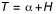 .
.
On calcule ensuite, à partir de T, l'instant du phénomène en temps universel comme on l'a expliqué dans les paragraphes précédents.
Si l'astre se déplace rapidement sur la sphère céleste (c'est le cas pour le Soleil, certaines planètes et surtout la Lune), on calcule pour l'instant trouvé des coordonnées α et δ plus exactes en interpolant les tables et l'on recalcule H puis T, par les formules (1) et (2), d'où l'instant du phénomène en UT. Pour la Lune, on est quelquefois amené à effectuer une itération supplémentaire.
Quant à h0, son expression générale est la suivante :
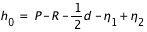 ,
,
P est la parallaxe. On la néglige pour tous les astres sauf pour la Lune pour laquelle P = 57'.
R est la réfraction à l'horizon. Les tables du présent volume utilisent la théorie de la réfraction de Radau qui conduit à R = 36'36", mais l'on pourra utiliser la valeur R = 34' adoptée dans les Ephémérides Nautiques publiées par le Bureau des longitudes et dans d'autres publications étrangères.
(1/2) d est le demi-diamètre apparent de l'astre. On l'introduit dans la formule quand on calcule le lever et le coucher du bord supérieur du Soleil et de la Lune et non pas le lever et le coucher du centre de l'astre. On prend, aussi bien pour le Soleil que pour la Lune, (1/2) d = 16'.
Si l'observateur est à une altitude A au-dessus du niveau de la mer, on introduit dans 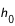 l'angle
l'angle 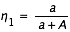 , où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
, où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
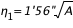 ,
,
A étant exprimé en mètres.
Si l'on cherche le lever ou le coucher d'un astre en un lieu dont l'horizon est limité par des collines ou des montagnes d'altitude 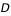 situées à la distance
situées à la distance 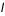 de l'observateur, on ajoutera à
de l'observateur, on ajoutera à 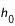 l'angle
l'angle 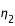 tel que :
tel que :
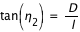 .
.
On ne cherchera pas à obtenir les instants du lever ou du coucher des astres avec une précision supérieure à une minute, la valeur exacte de la réfraction à l'horizon au moment du phénomène étant trop mal connue.
Coucher à Bordeaux de l'étoile Sirius le 20 Avril 2002.
Les coordonnées moyennes de l'étoile pour 2002 sont (chapitre 10, "Positions d'étoiles") :
α = 6h 45m 15s ; δ= - 16°43'11".
En faisant les corrections de précession pour le 20 avril (données à la fin de ce chapitre), on trouve :
α = 6h 45m 16s, δ = 16°43'12".
Ici P = 0, (1/2) d = 0, η1 = 0, η2 = 0 ;
d'où :
h0 = -R = -34'
Les coordonnées de Bordeaux sont :
λ = + 2m 7s φ = + 44°50'7".
On déduit de la formule (1) :
cos H = 0,28411 d'où H = 73,494° = 4h 53m 59s.
Et le temps sidéral du coucher est :
T = α + H = 11h 39m 15s.
Le temps sidéral de Greenwich est donc :
T1 = T + λ = 11h 41m 22s
Le temps sidéral de Greenwich à 0h le 20 avril 2002 est T0 = 13h 51m 38s (chapitre "Positions du Soleil et de la Lune").
d'où :
Tt = T1 - T0 = 21h 49m 44s.
En convertissant cet intervalle de temps sidéral en un intervalle de temps moyen, on trouve que Sirius se couche à Bordeaux le 20 avril 2002 à :
t = 21h 46m 9s (UT)
Les satellites galiléens présentent des phénomènes particuliers dus aux positions que prennent le Soleil, Jupiter et la Terre : les éclipses (lorsqu'un satellite passe dans l'ombre de Jupiter) ; les occultations (lorsqu'un satellite passe derrière Jupiter par rapport à la Terre) ; les passages (lorsqu'un satellite passe devant Jupiter par rapport à la Terre) et les passages d'ombre (lorsque l'ombre d'un satellite passe sur le disque de Jupiter). Les phénomènes les plus célèbres sont les éclipses car ils sont les plus faciles à observer : il s'agit de l'extinction ou de l'apparition d'un satellite isolé. Les autres phénomènes nécessitent l'observation simultanée de Jupiter ce qui dégrade beaucoup le rapport signal sur bruit.
Tous ces phénomènes ont été observés visuellement pendant des dizaines d'années et le grand nombre d'éclipses observées a constitué la base des premières éphémérides. Dès la fin du XIXème siècle, les techniques d'observation des éclipses se sont améliorées et les premières courbes photométriques ont permis d'améliorer la précision de la datation de ces phénomènes. Ensuite, les enregistreurs photoélectriques sont apparus mais, malgré le progrès qu'ils apportaient, ils ont été très peu utilisés : ils sont arrivés lorsque cessa l'intérêt des astronomes pour ce type de travaux et n'ont pas encore été repris pour des raisons de précision.
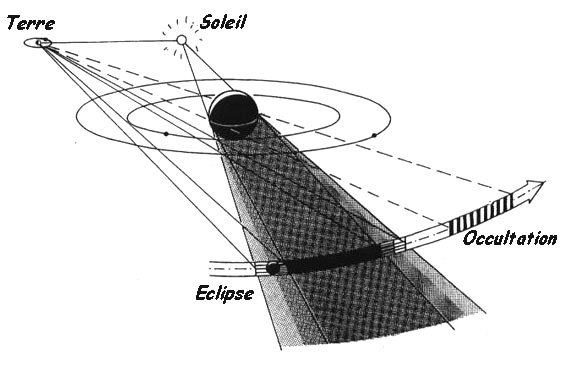
Les positions relatives de Jupiter, du Soleil et de la Terre pour que les satellites galiléens présentent des "phénomènes".
Crédit :
I.M.C.C.E./D.T. VU
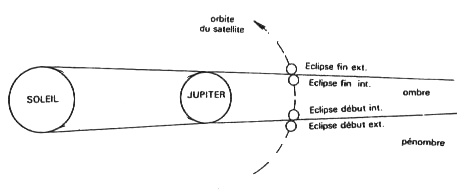
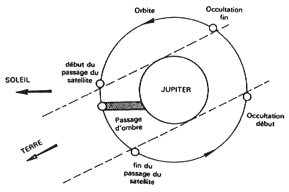
Configurations pour les différents types de phénomènes.
Crédit :
I.M.C.C.E./W. THUILLOT

Un passage d'ombres sur le disque de Jupiter.
Crédit :
Karkoshka et Murrell, NMSU
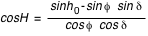 où
où
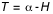 ;
;
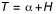 .
.
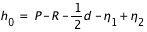 ,
,
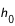 l'angle
l'angle 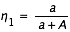 , où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
, où a est le rayon de la Terre. On prend a = 6 378 140 m. On peut utiliser la formule approchée :
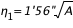 ,
,
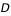 situées à la distance
situées à la distance 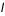 de l'observateur, on ajoutera à
de l'observateur, on ajoutera à 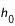 l'angle
l'angle 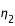 tel que :
tel que :
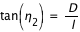 .
.



