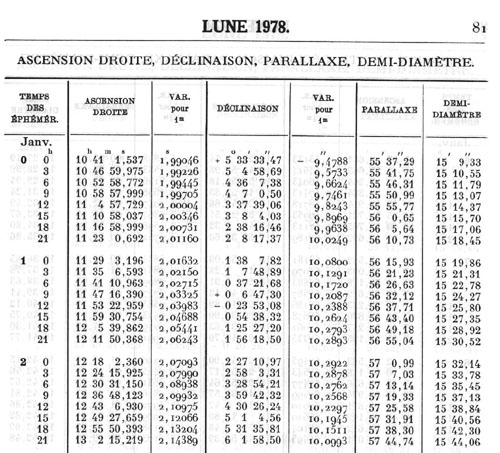
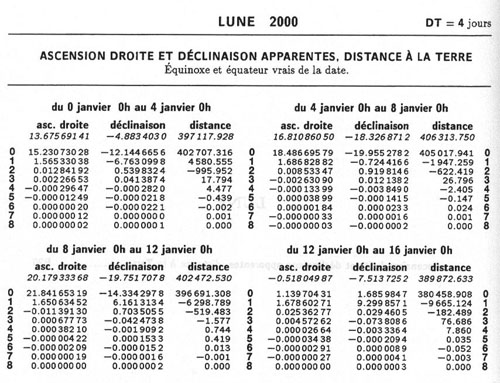
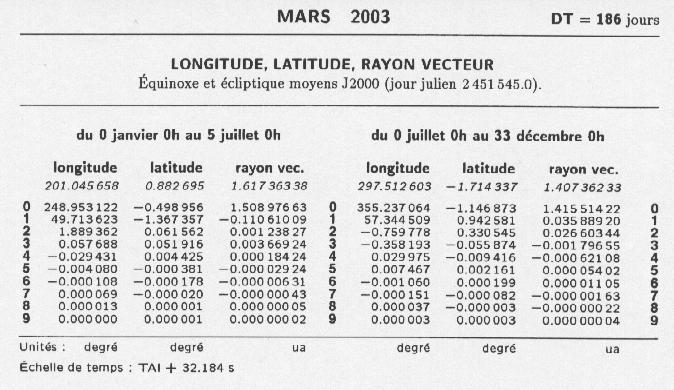
La plus ancienne forme sous laquelle les éphémérides fournissent les positions des astres est une table de positions dont l'intervalle (une heure, un jour, un mois, ...) dépend de la vitesse de variation des valeurs de ces positions. Plus cette variation est rapide, plus petit doit être l'intervalle de temps séparant deux données successives. La simple lecture d'une table, accompagnée d'une interpolation à vue, suffit pour fournir une position permettant de repérer l'astre dans le ciel. Cependant, si l'on souhaite une précision plus grande, il faut effectuer une interpolation qui n'est plus linéaire, ce qui demande des calculs plus complexes à partir des valeurs publiées si celles-ci le permettent. Pour une précision plus grande, il faut diminuer l'intervalle entre deux positions et donc augmenter le volume de données publiées. L'Astronomical Almanac et le Guide des données astronomiques encore aujourd'hui, et la Connaissance des Temps jusqu'en 1979, contiennent des éphémérides sous forme de telles tables.
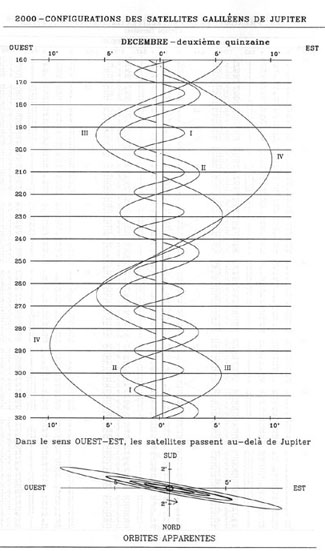
Citons le cas de la Lune : pour une précision de 0.01 seconde de degré, l'intervalle entre deux positions doit être de 3 heures ce qui conduit à la publication de 2920 valeurs annuellement par coordonnée. Citons aussi le cas des satellites galiléens de Jupiter qui ont un mouvement extrêmement rapide autour de Jupiter. Une éphéméride tabulée aurait nécessité un pas toutes les 20 minutes soit près de 30 000 valeurs pour une année! Cela conduit à un volume de données trop important pour être publié tel quel dans une éphéméride imprimée. D'autres solutions doivent être trouvées.
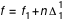
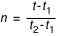 et
et 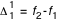

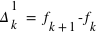
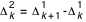 {k=0,1,2,...}
{k=0,1,2,...}
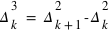
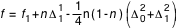
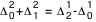

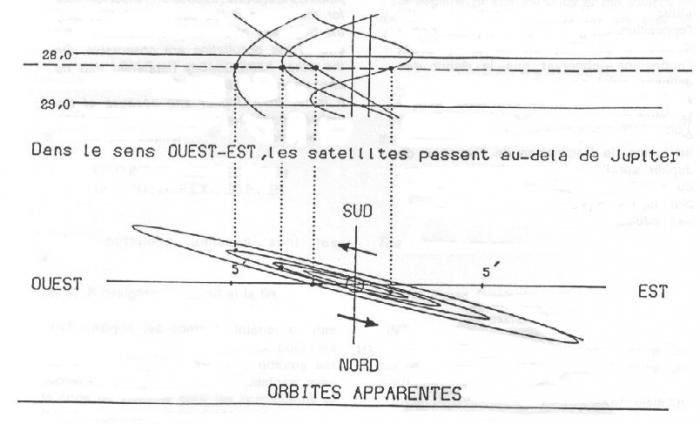
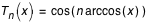
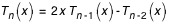 avec
avec 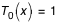 et
et 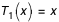
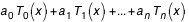
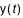 par la formule :
par la formule :
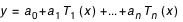
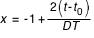
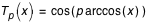 ;
; 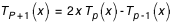 Avec :
Avec : 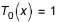 ;
; 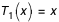
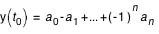
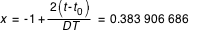
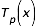 sont calculés par la relation (3) :
sont calculés par la relation (3) :
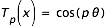 où
où 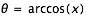
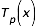 sont calculés par la relation de récurrence (4) :
sont calculés par la relation de récurrence (4) :
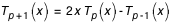
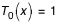 ;
; 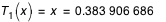
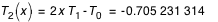 ,
,
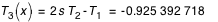 , etc
, etc
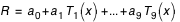 ,
,
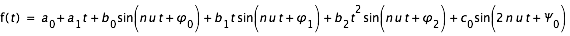 .
.
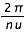 est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les
est une période proche de la période de révolution du corps ; les aj, bj, cj, sont les amplitudes, ; les 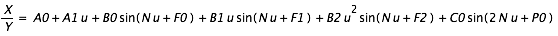 (5),
(5),
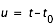 (u est compté en jours).
(u est compté en jours).
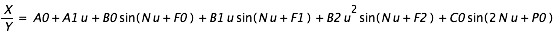 ,
,
