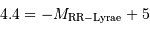SOLUTION

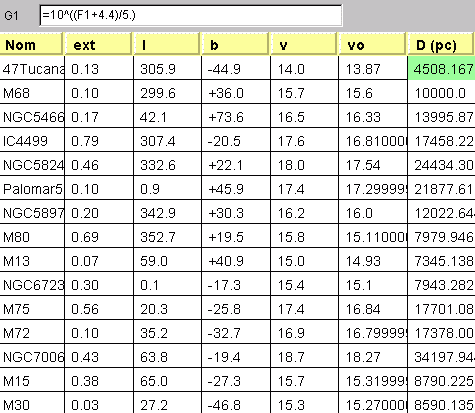
Le calcul de la distance peut se mener avec l'appliquette, en application directe de la définition du module de distance. On procède ainsi :

- sélection de la colonne G (variable D), en cliquant sur G1 - introduction dans la ligne de commande de {=10^((F1+4.4)/5.)} ou {=10^((vo+4.4)/5.)}, avec F1 la colonne représentant la magnitude corrigée de l'extinction, et 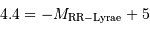$4.4= -M _{\mathrm{RR-Lyrae}}+5$ .

Crédit : ASM

Le calcul d'incertitude se mène en différenciant l'équation du module de distance :

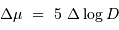
$\Delta \mu\ =\ 5\ \Delta \log D$

En prenant garde à la différence en bases du logarithme :

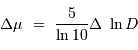
$\Delta \mu \ = \ {5\over \ln 10} \Delta\ \ln D$

Avec, d'après l'énoncé, 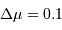$\Delta\mu = 0.1$ :

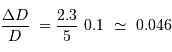
$\frac{\Delta D}{D}\ = \frac{2.3}{5}\ 0.1\ \simeq\ 0.046$

Soit une erreur de l'ordre de 5% qui, à 10 kpc, représente une incertitude de 500 pc.