SOLUTION

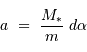
On traite l'équation :

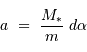
$a\ =\ { M _{\mathrm{*}}\over m}\ d\alpha$

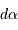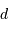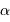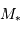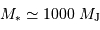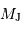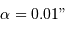en tenant en compte que le produit $d\alpha$ , avec en pc et $\alpha$ en " donne une distance en UA directement, par définition. En prenant $M _{\mathrm{*}}$ directement en masse jovienne ( $M _{\mathrm{*}}\simeq 1000\ M _{\mathrm{J}}$ ), on obtient dans le système d'unités (UA, $M _{\mathrm{J}}$ ), pour $\alpha=0.01"$ :

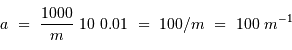
$a \ = \ {1000\over m} \ 10 \ 0.01 \ = \ 100 /m\ = \ 100 \ m^{-1}$

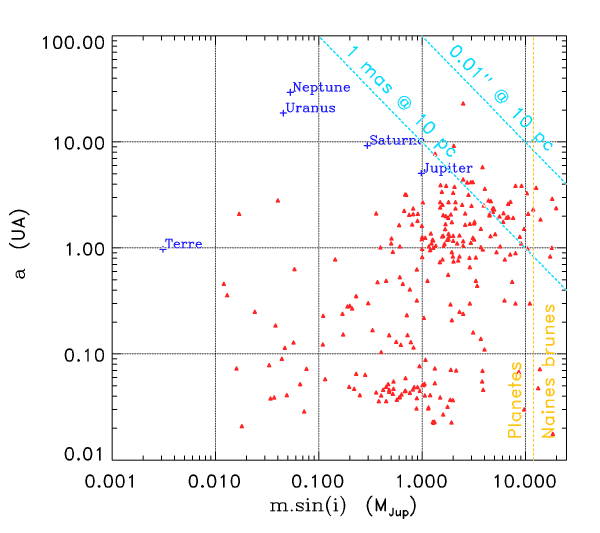
En échelle logarithmique, cette équation définit une droite de pente -1 ; elle passe par le point 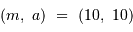$(m, \ a) \ = \ (10, \ 10)$ .

Pour une précision de 1 mas (1 millième de seconde d'arc), la courbe obtenue est définie par :

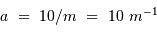
$a \ = \ 10 /m\ = \ 10 \ m^{-1}$

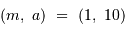Parallèle à la précédente, elle contient le point $(m, \ a) \ = \ (1, \ 10)$ .

Comme le montre le diagramme ci-joint, aucune planète du système solaire n'est ainsi détectable à ce niveau de précision astrométrique.

Diagramme a-msin i

Crédit : ASM