L'expansion de l'univers décrite au précédent chapitre révèle un univers régi par les lois de la relativité générale confortant la théorie du Big Bang. L'expansion prédit que la lumière qui nous parvient des galaxies éloignées est décalée vers les grandes longueurs d'onde, vers le rouge. Donc regarder à de grandes longueurs d'onde, c'est pouvoir regarder les galaxies dans le passé. Cependant d'après la théorie du Big Bang, au début de l'univers, il y a plus de 13 milliards d'années, il n'y avait pas de galaxies, il n'y avait qu'un plasma mêlant de la lumière en interaction avec de la matière. Ce chapitre traite de la signature observationnelle de cette époque en présentant le Fond Diffus Cosmologique (FDC). Alors que nos instruments modernes détectent difficilement des galaxies à des décalages spectraux plus grands que 4, la lumière du Fond Diffus Cosmologique nous parvient d'un décalage spectral de près de 1 100, décalée à des longueurs d'onde si grandes, de l'ordre du centimètre, que nos yeux ne peuvent la percevoir. Cette lumière des tous premiers âges de notre univers est une ressource irremplaçable pour comprendre l'état de la matière au début de l'univers (380 000 ans) : un plasma quasi-homogène à l'équilibre, d'une température de près de 3 000 K. Plusieurs sondes ont cartographié cette lumière, la dernière en date, encore active, est la sonde Planck qui délivra ses premiers résultats en mars 2013.
Le radiotélescope de Holmdel

Radio télescope de Holmdel (laboratoires Bell Labs) ayant permis à Penzias et Wilson la découverte du fond diffus cosmologique.
Crédit :
Bell Labs
Jusqu'à la seconde guerre mondiale, les observations astronomiques étaient limitées aux longueurs d'onde visibles. Pendant la seconde guerre mondiale, la technologie des radars a énormément évolué, en premier lieu pour des applications militaires, puis pour des applications civiles avec le retour de la paix. Durant les années 1959 - 1961, un cornet de 6 m a été construit aux États-Unis, installé sur la colline de Crawford, à Holmdel dans le New Jersey par le Bell Telephone Laboratory, pour recevoir le signal du satellite Echo puis Telstar.
En 1963, ce cornet a été transformé en radiotélescope par Alan A. Penzias et Robert W. Wilson pour observer le halo de notre Galaxie à la longueur d'onde d'environ 7,35 cm. Durant leurs observations pendant les années 1963 - 1965, Penzias et Wilson ont détecté un signal supérieur à celui prévu. Ils ont d'abord cherché à mieux estimer les contributions "parasites" qui pouvaient être dues au ciel, à l'antenne, au guide d'onde, aux détecteurs. Mais toutes ces contributions étaient trop faibles pour pouvoir rendre compte de l'excès observé. De plus, le signal observé était identique dans toutes les directions, donc ne pouvait pas provenir de sources ponctuelles. Il était aussi constant dans le temps. En résumé, nous baignons dans un flux permanent de photons de grandes longueurs d'onde.
Dans le but de tenter de comprendre le phénomène observé, Penzias et Wilson ont alors pris contact avec des théoriciens (Dicke, Peebles, Roll, Wilkinson) de l'Université de Princeton, l'une des meilleures Universités des États-Unis. Deux premiers articles ont paru en 1965 dans la revue américaine The Astrophysical Journal (volume 142, pages 414 et 419) présentant la découverte et l'interprétation de ce rayonnement comme étant un "fond diffus cosmologique", que nous noterons désormais FDC.
Leur interprétation était la suivante : le FDC est le résidu d'un rayonnement émis par l'Univers lorsqu'il était dans une phase très chaude et dense. Un tel rayonnement avait été prédit par Lemaître dans les années 1920, puis par Gamow, Alpher et Herman dans les années 1950. Ce rayonnement aurait été émis par l'univers tout entier environ 380 000 ans après le Big Bang et aurait aujourd'hui un spectre de corps noir à la température de quelques Kelvin, refroidi par l'expansion de l'univers.
L'observation de ce rayonnement qui sera détaillée et expliquée dans ce chapitre est l'argument le plus fort en faveur du modèle du Big Bang.
Avant la recombinaison
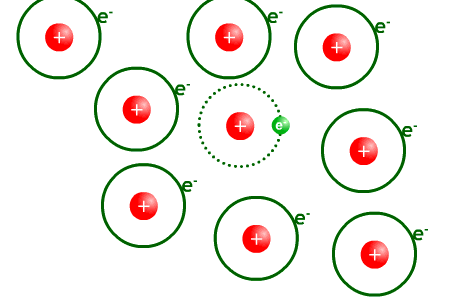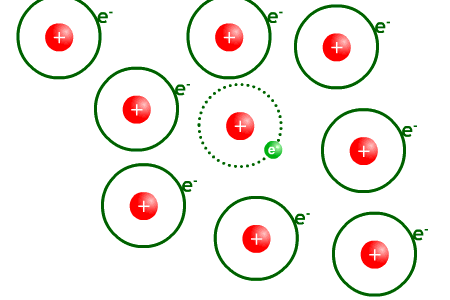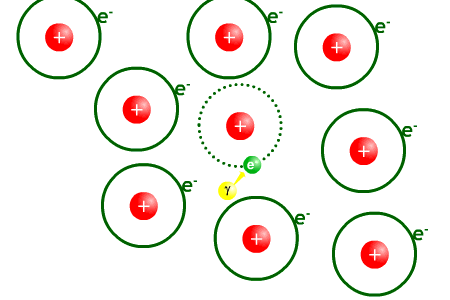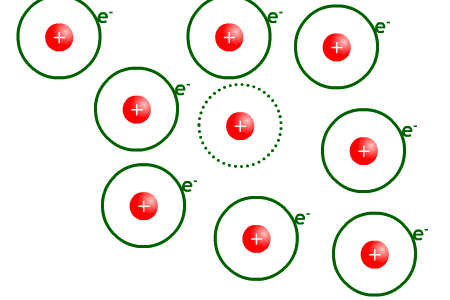
Univers opaque. Les photons sont arrêtés par la matière en interagissant avec cette dernière.
Crédit :
Astrophysique sur Mesure / Florence Durret et Gilles Bessou
Après la recombinaison
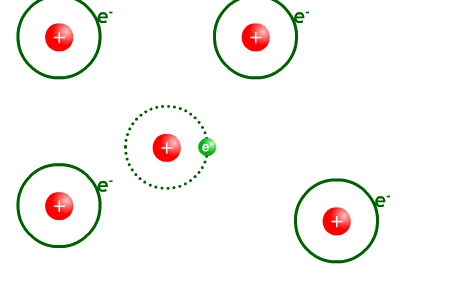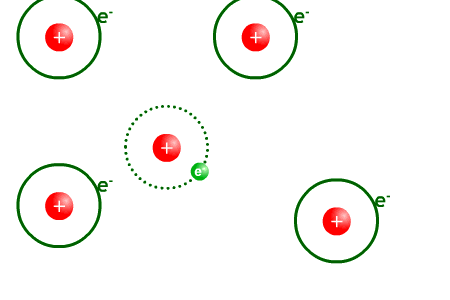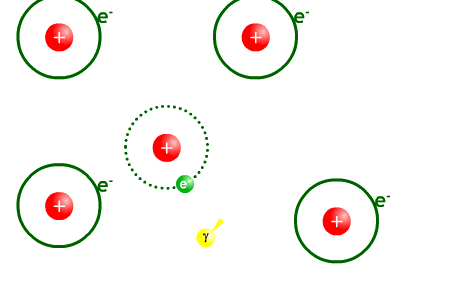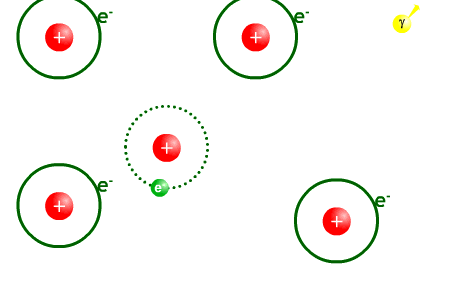
Univers transparent. Les photons moins énergétiques n'interagissent plus avec la matière, ils peuvent se déplacer sur de longues distances.
Crédit :
Astrophysique sur Mesure / Florence Durret et Gilles Bessou
Avant de décrire plus en détail les propriétés du FDC, ce dernier doit être remis dans son contexte cosmologique afin d'être bien compris. Pour cela, il faut revenir à près de 380 000 ans après le Big Bang, quand l'univers était très jeune.
Avant la recombinaison
A cette époque qui correspond à un décalage spectral de 1 100, l'univers était bien différent de celui que l'on connaît aujourd'hui : pas de structure cosmologique, pas de galaxie ni même d'étoile ou de molécule. L'univers âgé de 380 000 ans était constitué essentiellement de photons, de noyaux d’hydrogène et d’hélium ainsi que d'électrons. L'univers était un plasma en équilibre thermique à la température de plus de 3 000 K où les photons interagissaient violemment et rapidement avec les électrons, les protons et les quelques autres noyaux atomiques formés alors (hélium en grande majorité). Cet équilibre thermique à plus de 3 000 K conditionne l'énergie des photons qui est rassemblée autour d'une énergie moyenne, c'est le modèle du corps noir qui sera vu par la suite. Cette énergie moyenne était si grande à cette époque qu'elle pouvait arracher un électron lié à un proton. Dans ces conditions, la lumière ne pouvait pas se propager librement, l’Univers était donc complètement opaque, et les noyaux atomiques ne pouvaient pas se combiner avec les électrons. On ne peut donc pas observer ce qui a pu se passer durant et avant cette période, car aucun photon n’a pu s’en échapper pour parvenir jusqu'à la Terre, tout comme il est impossible de voir à travers un épais brouillard.
Après la recombinaison
Passés 380 000 ans après le Big Bang, l’expansion de l’Univers fait chuter la température de l'univers en dessous de 3 000 K. Les photons perdent alors de l'énergie via l'augmentation de leur longueur d'onde due à l'expansion de l'univers (voir le chapitre sur l'expansion de l'univers). Ils ne peuvent plus arracher d'électrons aux atomes, il n'y a plus d'interaction entre les photons et les noyaux. Les photons alors se découplent de la matière et peuvent parcourir des distances infinies. L'univers devient alors transparent. De leur côté, les noyaux atomiques peuvent enfin se combiner avec les électrons pour donner des atomes d’hydrogène et d'hélium neutre : c’est la phase dite de recombinaison bien qu'il n'y ait jamais eu de phase de combinaison. A la suite de cette phase, les photons libres constituent le FDC (aussi appelé rayonnement « fossile »). Avec l’expansion de l’Univers, la longueur d'onde de ces photons continue à augmenter et leur énergie à diminuer. Il en est de même de la température du corps noir correspondant ; de 3 000 K au moment de la recombinaison la température est tombée actuellement (13,7 milliards d'années après l’émission du FDC) à 2,728 K.
Courbes de luminosité de corps noirs
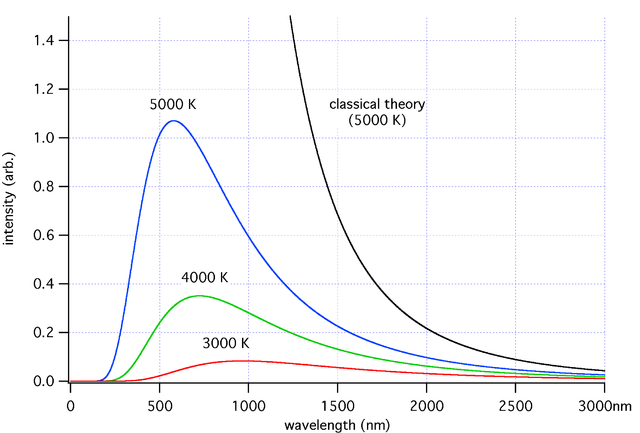
Exemple de courbes de luminosité pour trois corps noirs de températures différentes. On reconnaît la forme de cloche des courbes des corps noirs. La courbe noire représente la courbe de luminosité en mécanique classique sans tenir compte des quanta ; elle se révèle fausse aux petites longueurs d'onde. Plus la température est grande plus le pic est décalé vers les faibles longueurs d'onde. Cela illustre la loi de Wien.
Exemple de spectres d'étoiles
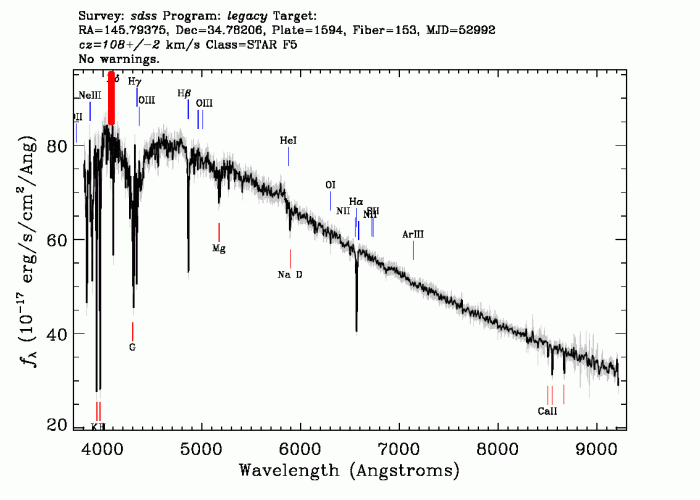
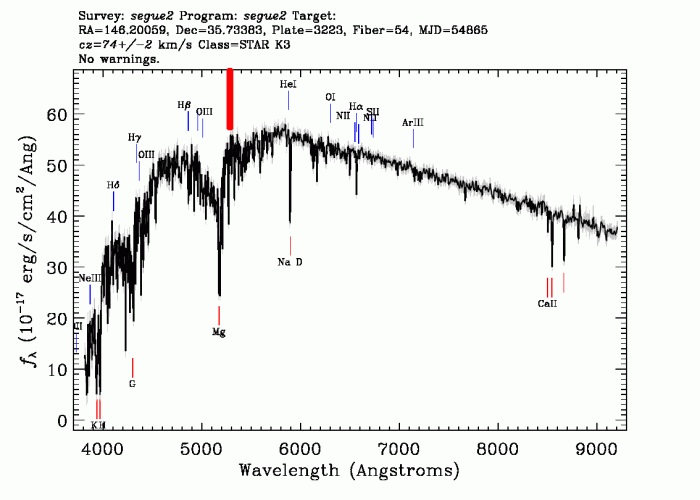
Exemples de spectres d'étoiles ayant des températures différentes. On y reconnaît deux spectres de corps noirs avec en plus des raies d'absorption et d'émission. Le pic est indiqué par un trait rouge. En haut, le pic n'est pas clairement visible (attention à ne pas le confondre avec la raie d'absorption), la température est de plus de 10 000 K. En bas, le pic semble être à 530 nm, la température avoisine les 5400 K.
Le FDC est un rayonnement issu d'un univers dense et chaud lequel peut être modélisé par un corps noir. Afin de comprendre les propriétés de ce reliquat des premiers temps, il faut connaître les propriétés des corps noirs et de leur rayonnement.
Définition d'un corps noir
La branche de la physique qui étudie les propriétés liées à la température des corps et aux échanges d’énergie entre eux (échanges de chaleur, émissions de rayonnement) s’appelle la thermodynamique. Un corps noir y est défini comme un corps en équilibre thermodynamique qui absorbe tout le rayonnement électromagnétique qu’il reçoit, contrairement à un miroir par exemple. Noir ne signifie pas qu'il est invisible comme un trou noir mais qu'il absorbe toute la lumière. En raison de sa température, un corps noir émet un rayonnement dit thermique qui est caractérisé par sa température. Le nombre de photons produits en fonction de leur longueur d'onde est une fonction qui a une forme de cloche asymétrique. Le pic de ce rayonnement est directement lié à sa température par la loi de Wien :
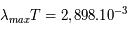 m.K
m.K
Ainsi le corps humain, qui est à une température d’environ 37°C (soit environ 37+273 = 310 K) émet un rayonnement principalement dans l’infrarouge à 9,3 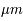 (d’où les jumelles à infrarouge utilisées pour repérer des êtres humains la nuit). La température étant inversement proportionnelle à la longueur d'onde du pic d'émission, plus un corps est chaud, plus son rayonnement a lieu vers les hautes énergies, c’est à dire vers les petites longueurs d’onde. Ainsi au fur et à mesure que l’on chauffe un morceau de fer il apparaîtra d’abord rouge, puis orange, et enfin bleu, diminuant sans cesse de longueur d'onde. Passée une certaine température, le pic se trouvera dans l'ultra-violet et l'oeil ne verra que la queue de distribution des photons des grandes longueurs d'onde.
(d’où les jumelles à infrarouge utilisées pour repérer des êtres humains la nuit). La température étant inversement proportionnelle à la longueur d'onde du pic d'émission, plus un corps est chaud, plus son rayonnement a lieu vers les hautes énergies, c’est à dire vers les petites longueurs d’onde. Ainsi au fur et à mesure que l’on chauffe un morceau de fer il apparaîtra d’abord rouge, puis orange, et enfin bleu, diminuant sans cesse de longueur d'onde. Passée une certaine température, le pic se trouvera dans l'ultra-violet et l'oeil ne verra que la queue de distribution des photons des grandes longueurs d'onde.
Exemple de corps noirs en astrophysique
Les poussières dans le milieu interstellaire sont un exemple de corps noir dont la température est de quelques centaines de Kelvin. Elles émettent principalement à des longueurs d'onde dans l'InfraRouge. Les étoiles dont la température superficielle peut prendre des valeurs entre quelques milliers et quelques dizaines de milliers de Kelvin sont aussi des corps noirs (voir figure). Leurs pics d'émission se situent entre 1000 et 100 nm. A noter que l'atmosphère des étoiles crée des raies d'émission et d'absorption dans le spectre d'une étoile, ce qui l'éloigne du corps noir parfait. Cependant, elles restent de meilleurs corps noir que le corps humain ou le fer.
Auteur: Sylvain Fouquet
 Exercice sur le corps noir
Exercice sur le corps noir
Un corps noir à la température 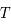 émet un rayonnement qui dépend de sa température et dont l'intensité
émet un rayonnement qui dépend de sa température et dont l'intensité 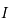 en fonction de la longueur d'onde est visualisée par l'applet suivant :
en fonction de la longueur d'onde est visualisée par l'applet suivant :
Le rayonnement du corps noir 
Question 1)
De quel côté de l'échelle en longueur d'onde se trouve l'ultraviolet ? l'infrarouge ?
Question 2)
Dans quel domaine de longueur d'onde un corps assimilable à un corps noir à la température ambiante émet-il ?
Question 3)
Qu'est-ce qui est le plus chaud : une une étoile rouge ou une étoile bleue ?
Question 4)
Quand on augmente la température d'un corps, le maximum d'émission se déplace-t-il vers les plus grandes longueurs d 'onde ?
Question 5)
En décochant "normaliser", l'échelle des ordonnées est maintenant absolue, c'est-à-dire qu'elle va de zéro au maximum d'intensité pour une température de 30 000K. Un corps à 15 000 K est-il plus ou moins lumineux qu'un corps à 5000 K ?
Spectre du Fond Diffus Cosmologique
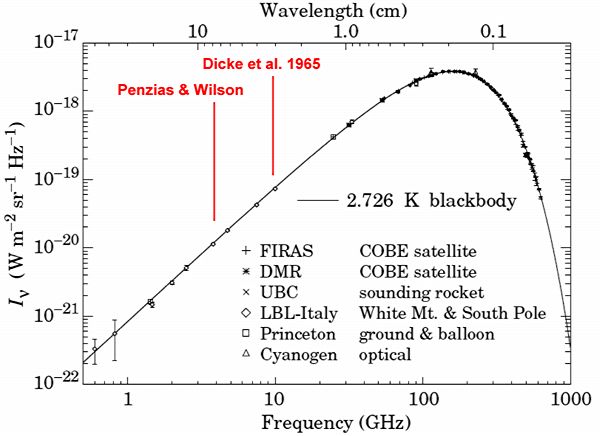
Spectre du FDC obtenu avec divers instruments au sol et dans l’espace. Les points correspondent aux observations, la courbe en pointillés correspond à l’émission théorique d’un corps noir à la température de 2,728 K. On remarque l’accord excellent avec les points d’observation sur trois ordres de grandeur en fréquence et quatre ordres de grandeur en intensité. Attention, les petites longueurs d'onde (wavelength) sont ici du côté gauche et non droite.
Crédit :
Site web de
l'APC de Paris VII.
Le FDC a été émis par l'univers quand il était sous la forme d'un plasma. L'univers à cette époque était un corps noir d'une température de près de 3 000 K. Le FDC est donc le spectre de ce corps noir mais décalé vers le rouge. En mesurant les propriétés de ce spectre, il est possible de connaître la température actuelle du FDC qui est de 2,728 K. En faisant le lien entre la température du FDC aujourd'hui et à l'époque de la recombinaison via le décalage spectral, on trouve un redshift de près de 1 100 pour l'époque de la recombinaison, que l'on associe à un âge de 380 000 ans après le Big Bang dans le modèle 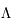 CDM.
CDM.
L'image ci-jointe montre les mesures du flux du FDC pour différentes longueurs d'onde. Le pic se situe à proximité de 0,1 cm, ce qui équivaut d'après la loi de Wien à une température de 2,7 K. Penzias et Wilson avaient mesuré le FDC à 7,3 cm. L'intensité à cette longueur d'onde est près de 100 fois inférieure à celle du pic. L'utilisation de ballons stratosphériques et le manque de mesure terrestre à faible longueur d'onde sont dus à l'absorption d'une partie du FDC par l'atmosphère pour les faibles longueurs d'onde. Afin de résoudre ce problème et d'avoir une meilleure résolution spectrale et spatiale les missions suivantes d'observations du FDC se feront exclusivement dans l'espace.
Connaissant la loi de rayonnement du FDC, il est possible d'en déduire la densité volumique d'énergie et donc le nombre de photons dû au FDC par litre. Il est proche de 400 000, ce qui équivaut à 400 photons par 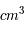 . Il est intéressant de le comparer aux nombres de particules massives, protons et neutrons. Ce dernier semble approcher les 0,5 atomes par litre. Cela conduit à un rapport de 1 particule massive pour 1 milliard de photons. Le nombre de particules et celui des photons du FDC n'ayant que peu évolué depuis la recombinaison, leur rapport est resté constant depuis plus de 13 milliards d'années.
. Il est intéressant de le comparer aux nombres de particules massives, protons et neutrons. Ce dernier semble approcher les 0,5 atomes par litre. Cela conduit à un rapport de 1 particule massive pour 1 milliard de photons. Le nombre de particules et celui des photons du FDC n'ayant que peu évolué depuis la recombinaison, leur rapport est resté constant depuis plus de 13 milliards d'années.
Le FDC par COBE
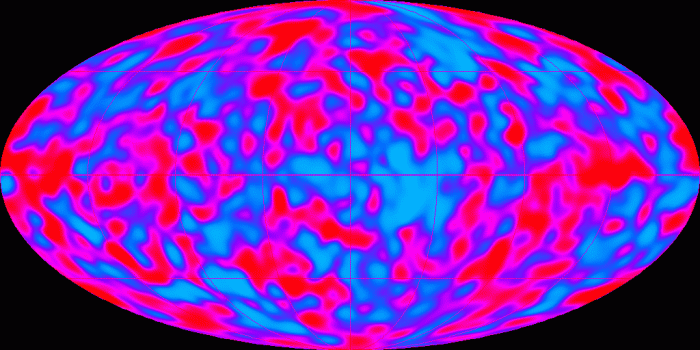
Le FDC vu par COBE après traitement des données. Les zones rouges sont les sur-densités, les zones bleues les sous-densités.
Le FDC par WMAP
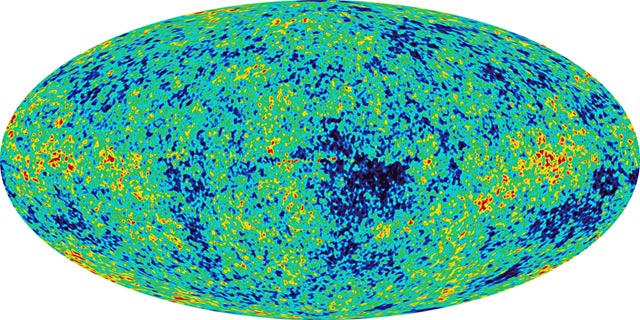
Le FDC vu par WMAP après traitement des données. Le gain de résolution spatiale comparé à COBE est évident. Les grandes structures sont retrouvées et des plus petites sont découvertes.
Le FDC par Planck
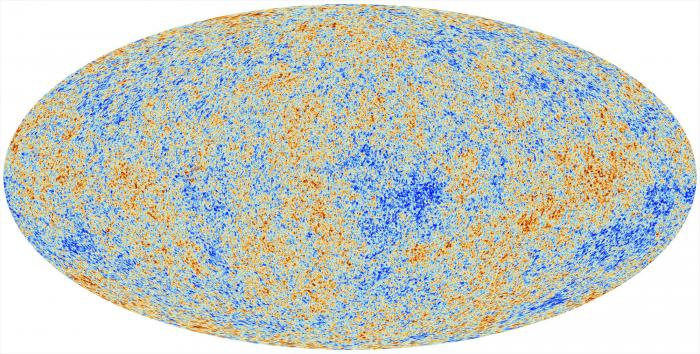
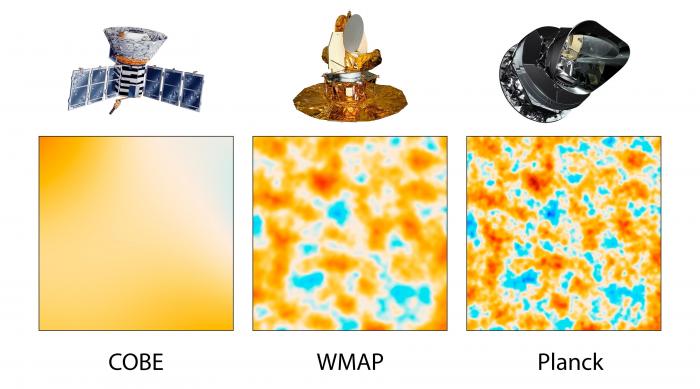
Le FDC vu par Planck après traitement des données. Le gain de résolution comparé à WMAP est moins flagrant. Ce n'est qu'en zoomant que l'on s'aperçoit du progrès accompli.
A basse résolution spatiale et de température, le FDC est isotrope (le même dans toutes les directions du ciel). Pourtant des anisotropies étaient attendues par le modèle théorique du FDC, de l'ordre de quelques 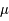 K,
K, 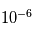 K. Les résultats du satellite COBE, Cosmic Background Explorer, ont été les premiers à mettre en évidence sur tout le ciel des fluctuations du FDC. Ces résultats ont ensuite été affinés par des expériences utilisant des ballons envoyés dans l'atmosphère qui couvraient des parties plus petites du ciel mais avec une meilleure résolution (Archeops et Boomerang). Des résultats spectaculaires sur tout le ciel sont obtenus par la sonde WMAP en 2003. Le satellite Planck, lancé en 2009, a encore permis un bond en avant dans l’étude du FDC.
K. Les résultats du satellite COBE, Cosmic Background Explorer, ont été les premiers à mettre en évidence sur tout le ciel des fluctuations du FDC. Ces résultats ont ensuite été affinés par des expériences utilisant des ballons envoyés dans l'atmosphère qui couvraient des parties plus petites du ciel mais avec une meilleure résolution (Archeops et Boomerang). Des résultats spectaculaires sur tout le ciel sont obtenus par la sonde WMAP en 2003. Le satellite Planck, lancé en 2009, a encore permis un bond en avant dans l’étude du FDC.
Plusieurs phénomènes peuvent expliquer les fluctuations du FDC. Il y a des raisons physiques dues à l'état de l'univers âgé de 380 000 ans qui n'était pas complètement isotrope (ceci cause des fluctuations dites primaires) et des interactions entre le FDC et les composantes de l'univers durant le voyage de treize milliards des photons pour parvenir à la Voie Lactée (ceci cause des fluctuations dites secondaires).
Certaines fluctuations primaires sont dues aux oscillations acoustiques. Dans l'univers chaud du début de l'univers, le fluide formé de photons, baryons et électrons oscille à la manière d'une onde acoustique. Le potentiel gravitationnel est contrebalancé par la force de pression de radiation, créant des bulles de légères sur-densités ou sous-densités. A la suite de la recombinaison la force de pression radiative due aux photons disparaît et les anisotropies sont figées. Ces oscillations du plasma primordial créent des changements dans la température donc dans le spectre du FDC et expliquent en partie ses anisotropies.
Certaines fluctuations secondaires sont dues à l'effet Sunyavev-Zel'dovich. Durant le long voyage des photons du FDC de leur lieu d'émission à la Voie Lactée, treize milliards d'années se sont écoulés et les photons ont parcouru une distance qui fait aujourd'hui près de 15 Gpc soit près de 50 milliards d'années lumière en prenant en compte l'expansion de l'univers (voir chapitre sur le continuum espace-temps de l'univers). Sur leur trajectoire, certains photons ont traversé des amas de galaxies formés bien après le Big-Bang. L'interaction (par diffusion) avec ce milieu rempli de gaz chaud et d'électrons libres a modifié leur température.
En définitif, les fluctuations de température mesurées sont de l'ordre de 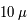 K en erreur absolue et donc de
K en erreur absolue et donc de 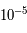 , 1 sur 100 000, en valeur relative. Le FDC a gardé l'empreinte du profil de densité de l'univers au moment du découplage lumière-matière.
, 1 sur 100 000, en valeur relative. Le FDC a gardé l'empreinte du profil de densité de l'univers au moment du découplage lumière-matière.
Auteur: Sylvain Fouquet
 Influence du mouvement du système solaire sur le FDC
Influence du mouvement du système solaire sur le FDC
Le FDC sans correction
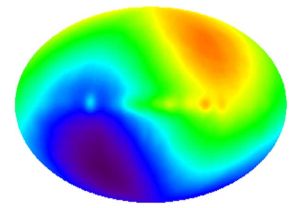
Le FDC sans la correction du mouvement de la terre. Cela crée un dipôle.
Crédit :
Differential Microwave Radiometer, Cosmic Background Explorer, NASA, Four-Year Sky Map
Le système solaire se meut dans le référentiel du FDC qui est en moyenne à 2,728 K. Cela donne lieu a un dipôle lorsque l'on observe le FDC (voir figure). Les parties qui se rapprochent de nous sont moins décalées vers le rouge que celles qui s'éloignent de nous. C'est l'effet Doppler classique.
Question 1)
Sachant que la différence de température entre les deux pôles peut atteindre près de 10 mK, quelle est la longueur d'onde minimale des photons du FDC comparé à celle moyenne ?
Question 2)
Quel redshift est déduit de cette compression de la longueur d'onde moyenne ?
Question 3)
Quelle est alors la vitesse du système solaire par rapport au FDC ?
Le spectre de puissance du FDC
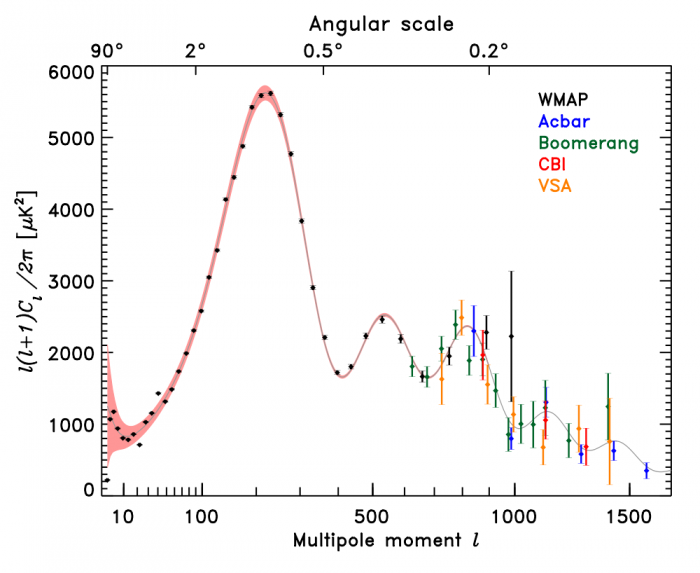
Spectre de puissance du FDC. En abscisse, ce sont les moments multipolaires, et, en ordonnée, leur intensité.
Crédit :
Wikipédia, creative commons
Le spectre de puissance du FDC
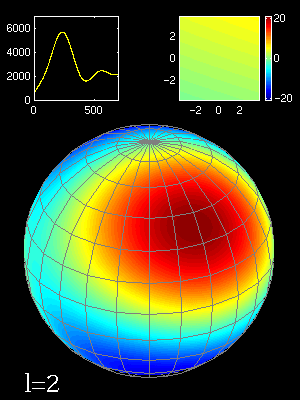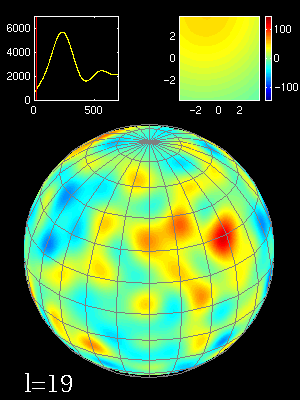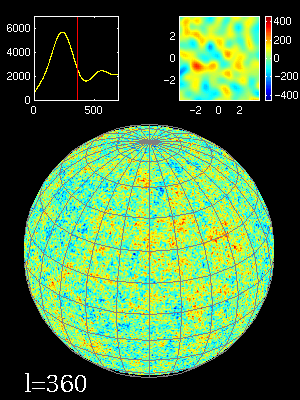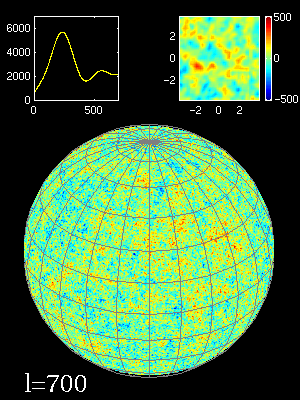
Animation montrant composition en moments multipolaires (indices

) des fluctuations angulaires sur la sphère céleste (une zone de 2°x2° est agrandie en haut à droite) et le spectre de puissance qui en résulte (en haut à gauche).
Crédit :
Site de l'APC,
APC
Définition du spectre de puissance
Après les images du FDC montrées dans la section précédente, il faut maintenant quantifier les inhomogénéités du FDC. Comment caractériser par des chiffres les anisotropies du FDC ? La méthode est de décomposer le FDC en une somme de moments multipolaires. Tout comme le nombre 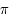 se décompose en la somme de 3 + 0.1 + 0.04 + 0.001 + 0.0005... le FDC peut se décomposer par une somme d'images ayant des résolutions spatiales de plus en plus grandes (voir l'animation). Le premier moment est une image homogène correspondant à un corps noir parfait sur tout le ciel de 2,728 K. Les autres images servent à affiner l'image pour retrouver l'image du FDC. Le résultat de cette décomposition s'appelle la loi de puissance du FDC. Elle donne l'intensité de chaque moment (voir graphique ci-joint). Les pics donnent une information sur la taille typique des anisotropies. Le premier pic est proche de 0,75°, c'est la taille typique des petites taches visibles sur la carte de WMAP. Elles seraient dues aux oscillations acoustiques de l'univers primordial.
se décompose en la somme de 3 + 0.1 + 0.04 + 0.001 + 0.0005... le FDC peut se décomposer par une somme d'images ayant des résolutions spatiales de plus en plus grandes (voir l'animation). Le premier moment est une image homogène correspondant à un corps noir parfait sur tout le ciel de 2,728 K. Les autres images servent à affiner l'image pour retrouver l'image du FDC. Le résultat de cette décomposition s'appelle la loi de puissance du FDC. Elle donne l'intensité de chaque moment (voir graphique ci-joint). Les pics donnent une information sur la taille typique des anisotropies. Le premier pic est proche de 0,75°, c'est la taille typique des petites taches visibles sur la carte de WMAP. Elles seraient dues aux oscillations acoustiques de l'univers primordial.
Déductions à partir de ce spectre
Le spectre de puissance est très important pour contraindre les paramètres cosmologiques. En effet, pour reproduire ce spectre dans le cadre du modèle 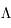 CDM, les paramètres cosmologiques sont ajustés : la densité de matière baryonique, celle de matière noire, la constante cosmologique, etc. Chaque mission d'observation du FDC (COBE, WMAP, Planck) a fourni et affiné la valeur des paramètres cosmologiques.
CDM, les paramètres cosmologiques sont ajustés : la densité de matière baryonique, celle de matière noire, la constante cosmologique, etc. Chaque mission d'observation du FDC (COBE, WMAP, Planck) a fourni et affiné la valeur des paramètres cosmologiques.
Les données ont montré que le FDC était très faiblement inhomogène ; une précision de l'ordre du 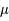 K est nécessaire pour déceler les anisotropies. Cette faible inhomogénité sur tout le ciel pose un problème. De fait, deux directions opposées lors de l'émission du FDC, il y a plus de 13 milliards d'années, étaient distantes de près 81 millions d'années lumière. Or l'univers n'ayant que 380 000 ans, il est impossible que ces deux zones aient pu interagir l'une avec l'autre pour établir un équilibre de quelques
K est nécessaire pour déceler les anisotropies. Cette faible inhomogénité sur tout le ciel pose un problème. De fait, deux directions opposées lors de l'émission du FDC, il y a plus de 13 milliards d'années, étaient distantes de près 81 millions d'années lumière. Or l'univers n'ayant que 380 000 ans, il est impossible que ces deux zones aient pu interagir l'une avec l'autre pour établir un équilibre de quelques 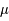 K à cause de l'existence d'une vitesse limite : la vitesse de la lumière. Ces infimes fluctuations pourraient être expliquées par une phase d'inflation de l'univers. Il s'agit d'une période au tout début de l'univers pendant laquelle l'univers aurait connu une expansion exponentielle. De ce fait, elle aurait transformé des inhomogénéités microscopiques en inhomogénéités macroscopiques.
K à cause de l'existence d'une vitesse limite : la vitesse de la lumière. Ces infimes fluctuations pourraient être expliquées par une phase d'inflation de l'univers. Il s'agit d'une période au tout début de l'univers pendant laquelle l'univers aurait connu une expansion exponentielle. De ce fait, elle aurait transformé des inhomogénéités microscopiques en inhomogénéités macroscopiques.






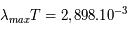 m.K
m.K
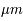 (d’où les jumelles à infrarouge utilisées pour repérer des êtres humains la nuit). La température étant inversement proportionnelle à la longueur d'onde du pic d'émission, plus un corps est chaud, plus son rayonnement a lieu vers les hautes énergies, c’est à dire vers les petites longueurs d’onde. Ainsi au fur et à mesure que l’on chauffe un morceau de fer il apparaîtra d’abord rouge, puis orange, et enfin bleu, diminuant sans cesse de longueur d'onde. Passée une certaine température, le pic se trouvera dans l'ultra-violet et l'oeil ne verra que la queue de distribution des photons des grandes longueurs d'onde.
(d’où les jumelles à infrarouge utilisées pour repérer des êtres humains la nuit). La température étant inversement proportionnelle à la longueur d'onde du pic d'émission, plus un corps est chaud, plus son rayonnement a lieu vers les hautes énergies, c’est à dire vers les petites longueurs d’onde. Ainsi au fur et à mesure que l’on chauffe un morceau de fer il apparaîtra d’abord rouge, puis orange, et enfin bleu, diminuant sans cesse de longueur d'onde. Passée une certaine température, le pic se trouvera dans l'ultra-violet et l'oeil ne verra que la queue de distribution des photons des grandes longueurs d'onde.
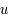 , ou le nombre de photon par unité de volume à la fréquence,
, ou le nombre de photon par unité de volume à la fréquence, 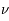 , des photons pour un corps noir d'une température
, des photons pour un corps noir d'une température 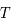 . Elle englobe la relation de Rayleigh-Jeans qui décrivait cette loi pour les grandes longueurs d'onde, au-delà du pic central de rayonnement. Elle est historiquement importante car la compréhension physique de la partie des courtes longueurs d'onde a requis l'ajout d'un concept nouveau en physique, le quantum d'énergie qui sera développé ultérieurement pour la mécanique quantique. Le loi de Planck est la suivante :
. Elle englobe la relation de Rayleigh-Jeans qui décrivait cette loi pour les grandes longueurs d'onde, au-delà du pic central de rayonnement. Elle est historiquement importante car la compréhension physique de la partie des courtes longueurs d'onde a requis l'ajout d'un concept nouveau en physique, le quantum d'énergie qui sera développé ultérieurement pour la mécanique quantique. Le loi de Planck est la suivante :
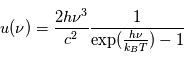
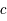 est la vitesse de la lumière (300 000 km/s),
est la vitesse de la lumière (300 000 km/s), 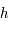 la constante de Planck (
la constante de Planck (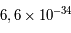 J.s) et
J.s) et 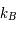 la constante de Boltzmann (
la constante de Boltzmann (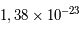 J/K).
J/K).
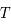 émet un rayonnement qui dépend de sa température et dont l'intensité
émet un rayonnement qui dépend de sa température et dont l'intensité 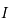 en fonction de la longueur d'onde est visualisée par l'applet suivant :
en fonction de la longueur d'onde est visualisée par l'applet suivant :


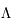 CDM.
CDM.
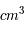 . Il est intéressant de le comparer aux nombres de particules massives, protons et neutrons. Ce dernier semble approcher les 0,5 atomes par litre. Cela conduit à un rapport de 1 particule massive pour 1 milliard de photons. Le nombre de particules et celui des photons du FDC n'ayant que peu évolué depuis la recombinaison, leur rapport est resté constant depuis plus de 13 milliards d'années.
. Il est intéressant de le comparer aux nombres de particules massives, protons et neutrons. Ce dernier semble approcher les 0,5 atomes par litre. Cela conduit à un rapport de 1 particule massive pour 1 milliard de photons. Le nombre de particules et celui des photons du FDC n'ayant que peu évolué depuis la recombinaison, leur rapport est resté constant depuis plus de 13 milliards d'années.




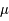 K,
K, 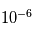 K. Les résultats du satellite COBE, Cosmic Background Explorer, ont été les premiers à mettre en évidence sur tout le ciel des fluctuations du FDC. Ces résultats ont ensuite été affinés par des expériences utilisant des ballons envoyés dans l'atmosphère qui couvraient des parties plus petites du ciel mais avec une meilleure résolution (Archeops et Boomerang). Des résultats spectaculaires sur tout le ciel sont obtenus par la sonde WMAP en 2003. Le satellite Planck, lancé en 2009, a encore permis un bond en avant dans l’étude du FDC.
K. Les résultats du satellite COBE, Cosmic Background Explorer, ont été les premiers à mettre en évidence sur tout le ciel des fluctuations du FDC. Ces résultats ont ensuite été affinés par des expériences utilisant des ballons envoyés dans l'atmosphère qui couvraient des parties plus petites du ciel mais avec une meilleure résolution (Archeops et Boomerang). Des résultats spectaculaires sur tout le ciel sont obtenus par la sonde WMAP en 2003. Le satellite Planck, lancé en 2009, a encore permis un bond en avant dans l’étude du FDC.
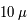 K en erreur absolue et donc de
K en erreur absolue et donc de 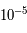 , 1 sur 100 000, en valeur relative. Le FDC a gardé l'empreinte du profil de densité de l'univers au moment du découplage lumière-matière.
, 1 sur 100 000, en valeur relative. Le FDC a gardé l'empreinte du profil de densité de l'univers au moment du découplage lumière-matière.



 ) des fluctuations angulaires sur la sphère céleste (une zone de 2°x2° est agrandie en haut à droite) et le spectre de puissance qui en résulte (en haut à gauche).
) des fluctuations angulaires sur la sphère céleste (une zone de 2°x2° est agrandie en haut à droite) et le spectre de puissance qui en résulte (en haut à gauche).
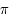 se décompose en la somme de 3 + 0.1 + 0.04 + 0.001 + 0.0005... le FDC peut se décomposer par une somme d'images ayant des résolutions spatiales de plus en plus grandes (voir l'animation). Le premier moment est une image homogène correspondant à un corps noir parfait sur tout le ciel de 2,728 K. Les autres images servent à affiner l'image pour retrouver l'image du FDC. Le résultat de cette décomposition s'appelle la loi de puissance du FDC. Elle donne l'intensité de chaque moment (voir graphique ci-joint). Les pics donnent une information sur la taille typique des anisotropies. Le premier pic est proche de 0,75°, c'est la taille typique des petites taches visibles sur la carte de WMAP. Elles seraient dues aux oscillations acoustiques de l'univers primordial.
se décompose en la somme de 3 + 0.1 + 0.04 + 0.001 + 0.0005... le FDC peut se décomposer par une somme d'images ayant des résolutions spatiales de plus en plus grandes (voir l'animation). Le premier moment est une image homogène correspondant à un corps noir parfait sur tout le ciel de 2,728 K. Les autres images servent à affiner l'image pour retrouver l'image du FDC. Le résultat de cette décomposition s'appelle la loi de puissance du FDC. Elle donne l'intensité de chaque moment (voir graphique ci-joint). Les pics donnent une information sur la taille typique des anisotropies. Le premier pic est proche de 0,75°, c'est la taille typique des petites taches visibles sur la carte de WMAP. Elles seraient dues aux oscillations acoustiques de l'univers primordial.
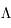 CDM, les paramètres cosmologiques sont ajustés : la densité de matière baryonique, celle de matière noire, la constante cosmologique, etc. Chaque mission d'observation du FDC (COBE, WMAP, Planck) a fourni et affiné la valeur des paramètres cosmologiques.
CDM, les paramètres cosmologiques sont ajustés : la densité de matière baryonique, celle de matière noire, la constante cosmologique, etc. Chaque mission d'observation du FDC (COBE, WMAP, Planck) a fourni et affiné la valeur des paramètres cosmologiques.
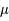 K est nécessaire pour déceler les anisotropies. Cette faible inhomogénité sur tout le ciel pose un problème. De fait, deux directions opposées lors de l'émission du FDC, il y a plus de 13 milliards d'années, étaient distantes de près 81 millions d'années lumière. Or l'univers n'ayant que 380 000 ans, il est impossible que ces deux zones aient pu interagir l'une avec l'autre pour établir un équilibre de quelques
K est nécessaire pour déceler les anisotropies. Cette faible inhomogénité sur tout le ciel pose un problème. De fait, deux directions opposées lors de l'émission du FDC, il y a plus de 13 milliards d'années, étaient distantes de près 81 millions d'années lumière. Or l'univers n'ayant que 380 000 ans, il est impossible que ces deux zones aient pu interagir l'une avec l'autre pour établir un équilibre de quelques 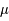 K à cause de l'existence d'une vitesse limite : la vitesse de la lumière. Ces infimes fluctuations pourraient être expliquées par une phase d'inflation de l'univers. Il s'agit d'une période au tout début de l'univers pendant laquelle l'univers aurait connu une expansion exponentielle. De ce fait, elle aurait transformé des inhomogénéités microscopiques en inhomogénéités macroscopiques.
K à cause de l'existence d'une vitesse limite : la vitesse de la lumière. Ces infimes fluctuations pourraient être expliquées par une phase d'inflation de l'univers. Il s'agit d'une période au tout début de l'univers pendant laquelle l'univers aurait connu une expansion exponentielle. De ce fait, elle aurait transformé des inhomogénéités microscopiques en inhomogénéités macroscopiques.