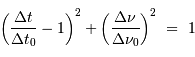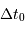SOLUTION

La région de la surface hermienne contribuant au début du signal d'écho est le point le plus proche de la Terre : le point subterrestre. La fin correspond aux dernières régions touchées : au limbe.

La durée totale théorique 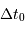$\Delta t_0$ de l'écho correspond à l'intervalle de temps pour parcourir radialement la planète du point subterrestre au limbe, càd parcourir son rayon :

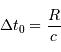
$\Delta t_0 = {R\over c}$

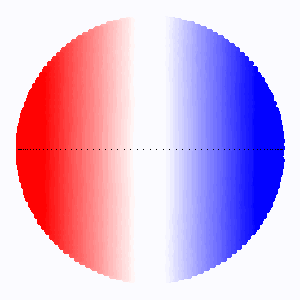
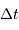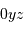Les lignes d'iso-retard $\Delta t$ sur la carte de Mercure [ 0yz ] sont des lignes à coordonnée 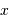fixée. Analytiquement, à la surface de la planète et dans le plan du ciel 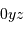0yz , l'équation

y^2+z^2 = R^2 - x^2

représente un cercle.

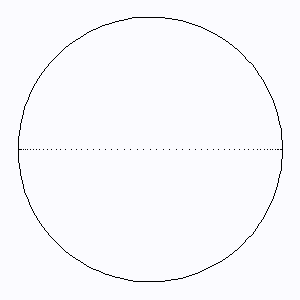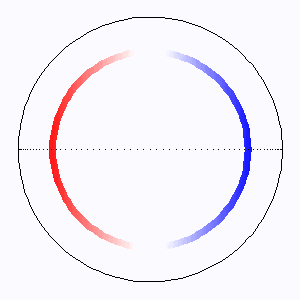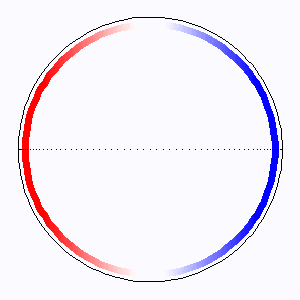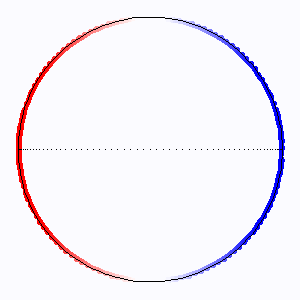
L'élargissement Doppler extrêmal est atteint au limbe, où l'entraînement rotationnel est le plus fort. Les lignes d'iso-fréquence correspondent aux lignes isovitesses : ce sont des droites parallèles à l'axe de rotation.

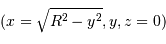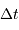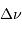Pour un point de Mercure de coordonnées $(x=\sqrt{R^{2}-y^{2}},y,z=0)$ , le retard $\Delta t$ de l'écho et son décalage spectral $\Delta\nu$ vérifient :

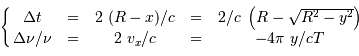
$\left\{ \matrix{ \Delta t &=& 2\ (R-x)/c &=& 2/c \ \left( R - \sqrt{R^2 - y^2}\right) \cr \Delta \nu/\nu &=& 2\ v_x / c &=& -4\pi \ y / cT \cr } \right.$

Les valeurs extrêmes du délai et du décalage sont :

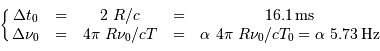
$\left\{ \matrix{ \Delta t_0 &=& 2\ R/c &=& 16.1 {\,\mathrm{ms}} \cr \Delta \nu_0 &=& 4\pi \ R\nu_0/ cT&=&\alpha\ 4\pi \ R\nu_0/ cT_0 = \alpha\ 5.73 {\,\mathrm{Hz}}\cr } \right.$

en ayant posé $T_0 = \alpha \ T$ . On en déduit, pour un point du plan équatorial ( z=0 ) :

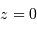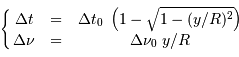
$\left\{ \matrix{ \Delta t &=& \Delta t_0\ \left(1 - \sqrt{1 - (y/R)^2}\right) \cr \Delta \nu &=& \Delta \nu_0 \ y/R\cr } \right.$

En éliminant la variable , il sort la relation demandée :

$\left( {\Delta t\over \Delta t_0} - 1\right)^2 +\left( {\Delta \nu\over \Delta \nu_0}\right)^2 \ = \ 1$