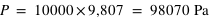Définition
Définition
La pression, 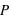 , est la force,
, est la force, 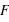 , rapportée à la surface,
, rapportée à la surface, 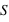 , sur laquelle elle s'applique,
, sur laquelle elle s'applique, 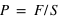 . Dans le système d'unités SI, un pascal (Pa) correspond à une force de
. Dans le système d'unités SI, un pascal (Pa) correspond à une force de 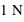 appliquée sur une surface de
appliquée sur une surface de 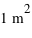 , et, est donc homogène à l'unité de base kg.m-1.s-2.
, et, est donc homogène à l'unité de base kg.m-1.s-2.
 La pression atmosphérique
La pression atmosphérique
L'atmosphère terrestre confinée par la force de gravité
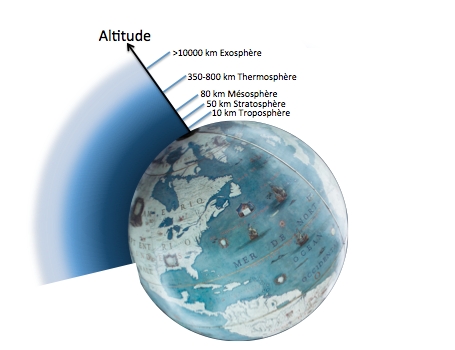
L'atmosphère terrestre est une couche de matière gazeuse confinée par la gravité de la Terre. Sa densité devient plus faible avec l'augmentation de l'altitude. Bien qu'il n'y ait pas une limite précise entre l'atmosphère et l'espace, en aéronautique ses effets sont considérés en dessous de 100 km d'altitude (dit aussi la ligne de Kármán). La navette spatiale internationale (ISS) est en orbite à une altitude d'environ 400 km, le Télescope Spatial Hubble (HST) l'est à 590 km ; ils orbitent dans la thermosphère.
Crédit :
ASM/Laurence Tresse (Globe terrestre de Coronelli, BnF)
 La sphère de Hill ou de Roche
La sphère de Hill ou de Roche
Difficulté : ☆
Question 1)
Calculer le rayon de la sphère de Hill de la Terre dans le champ de gravité du Soleil. Qu'en déduisez-vous pour la Lune ? pour la planète la plus proche Mars ?
On négligera l'influence des autres planètes et on exprimera le rayon en Unité Astronomique avec 1 U.A. = distance Terre-Soleil. On utilisera pour la Terre, 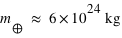 et pour le Soleil,
et pour le Soleil, 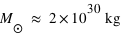 . La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.
. La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.
Question 2)
L'influence gravitationnelle du système solaire est estimée à 125000 U.A. Qu'en déduisez-vous pour l'étoile la plus proche du système solaire, Proxima du Centaure, située à 270000 U.A. environ ?
 Définition
Définition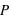 , est la force,
, est la force, 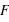 , rapportée à la surface,
, rapportée à la surface, 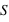 , sur laquelle elle s'applique,
, sur laquelle elle s'applique, 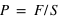 . Dans le système d'unités SI, un pascal (Pa) correspond à une force de
. Dans le système d'unités SI, un pascal (Pa) correspond à une force de 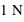 appliquée sur une surface de
appliquée sur une surface de 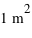 , et, est donc homogène à l'unité de base kg.m-1.s-2.
, et, est donc homogène à l'unité de base kg.m-1.s-2.
 La pression atmosphérique
La pression atmosphérique
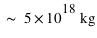 . Sachant que la superficie du globe terrestre vaut
. Sachant que la superficie du globe terrestre vaut 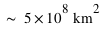 , combien vaut la masse moyenne au-dessus d'un mètre carré ?
, combien vaut la masse moyenne au-dessus d'un mètre carré ?
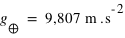 ), à quelle pression atmosphérique cela correspond-t-il ?
), à quelle pression atmosphérique cela correspond-t-il ?
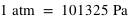 (valeur standard officielle). A votre avis pourquoi votre résultat précédent diffère de cette valeur ?
(valeur standard officielle). A votre avis pourquoi votre résultat précédent diffère de cette valeur ?
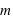 à une distance
à une distance 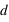 d'un corps plus massif de masse
d'un corps plus massif de masse 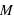 , le rayon de sa sphère de Hill vaut
, le rayon de sa sphère de Hill vaut ![r_H=d\, \sqrt[3]{\frac{m}{3M}}](../pages_forces/equations_force-gravitation-exercices-autre/equation17.png) .
.
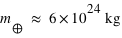 et pour le Soleil,
et pour le Soleil, 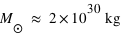 . La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.
. La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.
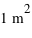 vaut
vaut 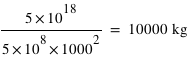 , soit environ 10 tonnes par mètre carré.
, soit environ 10 tonnes par mètre carré.