 Enoncé
Enoncé
Le Principe Fondamental de la Dynamique, qui dérive de la deuxième loi de Newton, énonce que l'accélération d'un corps est la résultante des forces qu'il subit : 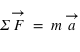 .
.
 Appplication
Appplication
Dans l'exercice précédent, nous avons négligé le fait que la Terre est légèrement aplatie au niveau des pôles, et la rotation autour de son axe, sans compter qu'elle est aussi une sphère avec un relief très varié... Etudions dans le prochain exercice leur prise en compte, en appliquant le principe fondamental de la dynamique, afin de mesurer localement la pesanteur terrestre.
Les variations locales de la pesanteur terrestre

La variation locale du champ de pesanteur terrestre illustré avec les données datant de juillet 2003 de la mission spatiale GRACE - du bleu foncé (le plus faible) au rouge foncé (le plus fort). La gravité standard à la surface de la Terre vaut, par convention,
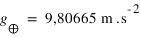
, elle prend en compte le rayon moyen de la Terre et la vitesse angulaire de la Terre à l'équateur. La sphère colorée représente ainsi les différences locales par rapport à la gravité standard de la Terre modélisée comme un ellipsoïde en rotation ayant une répartition de masse homogène.
Crédit :
University of Texas Center for Space Research and NASA
 Se libérer de la pesanteur...
Se libérer de la pesanteur...
Difficulté : ☆☆☆
Pour se libérer totalement de la pesanteur, la vitesse doit être au moins égale à : 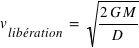 .
.
Question 1)
Combien vaut la vitesse de libération pour la Terre, Jupiter et le Soleil ?
Question 2)
Dans le cas d'un décollage vertical, quelle serait l'accélération (constante et linéaire) nécessaire pour faire passer un engin d'une vitesse nulle à la vitesse de libération terrestre (cf. question 1) sur une distance de 1000 km ? A combien de 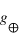 cela correspond-t-il ?
cela correspond-t-il ?
Question 3)
Pourquoi place-t-on les sondes spatiales d'abord en orbite basse 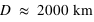 avant de les propulser plus loin pour aller explorer le système solaire ?
avant de les propulser plus loin pour aller explorer le système solaire ?
Question 4)
Quelle est l'expression de la vitesse de libération de l'influence gravitationnelle du Soleil à partir de la surface de la Terre ? Combien vaut-elle ?
- Question 1
Aide :
Lorsqu'un corps matériel, de masse 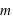 , a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
, a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
La force centrifuge dans le cas d'un mouvement circulaire uniforme vaut 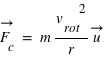 , où
, où 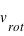 est la vitesse de rotation,
est la vitesse de rotation, 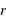 la distance entre la masse
la distance entre la masse 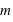 et le centre du cercle,
et le centre du cercle, 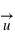 le vecteur unitaire dirigé du centre du cercle à la position de la masse.
le vecteur unitaire dirigé du centre du cercle à la position de la masse.
Pour le cas d'un corps matériel à la surface terrestre, noter bien que c'est le centre du cercle (qui se situe le long de l'axe de rotation terrestre), et non le centre de la sphère terrestre. Donc, aux pôles cette force est nulle : 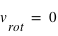 (le centre du cercle = pôle) , et à l'équateur elle est maximale (
(le centre du cercle = pôle) , et à l'équateur elle est maximale (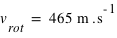 , le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
, le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
Solution :
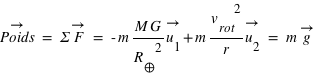 , avec
, avec 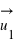 dirigé de la position de la masse
dirigé de la position de la masse 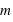 vers le centre de gravité de la Terre, et
vers le centre de gravité de la Terre, et 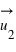 dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
- Question 2
Solution :
Non, sauf lorsque 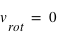 (aux pôles).
(aux pôles).
- Question 3
Aide :
Le rayon terrestre aux pôles vaut 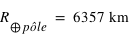 et à l'équateur
et à l'équateur 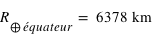 . La masse de la Terre vaut
. La masse de la Terre vaut 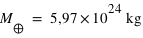 .
.
Solution :
Aux pôles, F = 60 x 6,674 x 10-11 x 5,97 1024/ 63570002 = 60 x 9,86 = 592 N, à l'équateur, F = 60 x 6,674 x 10-11 x 5,97 1024 / 63780002 - 60 x 4652/6378000 = 60 x 9,79 - 60 x 0,03 = 60 x 9,76 = 586 N. Une différence de 6 N parait négligeable, mais pour un objet de masse bien plus importante, telle une fusée, de plusieurs tonnes la différence signifie bien moins d'énergie à fournir au décollage, soit pour 300 tonnes, la différence de pesanteur est de l'ordre de ~ 30 000 N ! A proximité de l'équateur, la force à fournir est donc la plus faible ; c'est le cas du centre spatial de Kourou en Guyane.
- Question 4
Solution :
La force centrifuge l'emporterait sur la force de gravitation, les habitants aux alentours de l'équateur seraient expulsés de la Terre !
- Question 1
Aide :
Pour Jupiter : 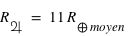 et
et 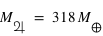 . Pour le Soleil :
. Pour le Soleil : 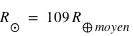 et
et 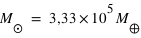 .
.
Solution :
Pour la Terre, Jupiter et le Soleil, vlibération = 11,2 km.s-1, 59 km.s-1 et 618 km.s-1, respectivement.
- Question 2
Aide :
L'accélération constante et linéaire, 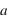 , qui fait passer un engin d'une vitesse nulle à une vitesse,
, qui fait passer un engin d'une vitesse nulle à une vitesse, 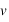 , sur une distance
, sur une distance 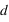 , vaut
, vaut 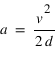 .
.
Solution :
v = 11,2 km.s-1 donc a = 11,22/ 2 x 1000 = 0,06272 km.s-2, soit ~63 m.s-2, soit ~6 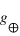 .
.
- Question 3
Solution :
Lorsqu'on met d'abord en orbite une sonde spatiale, on bénéficie du fait que la vitesse de libération est moindre à l'altitude 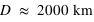 plutôt qu'à la surface de la Terre
plutôt qu'à la surface de la Terre 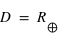 , et donc une force d'accélération,
, et donc une force d'accélération, 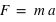 , bien moindre à fournir.
, bien moindre à fournir.
- Question 4
Aide :
On négligera l'influence des autres planètes. Les vitesses s'ajoutant au carré, soit 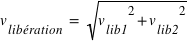 , où
, où 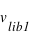 est la vitesse de libération de la Terre, et
est la vitesse de libération de la Terre, et 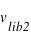 est la vitesse de libération du Soleil situé à
est la vitesse de libération du Soleil situé à 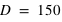 millions de kilomètres de la Terre. A cette vitesse
millions de kilomètres de la Terre. A cette vitesse 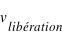 , il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil,
, il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil, 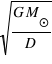 .
.
Solution :
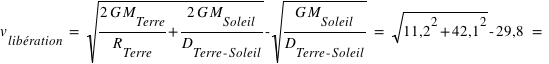 13,8 km.s-1.
13,8 km.s-1.
 Enoncé
Enoncé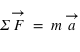 .
.
 Appplication
Appplication
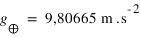 , elle prend en compte le rayon moyen de la Terre et la vitesse angulaire de la Terre à l'équateur. La sphère colorée représente ainsi les différences locales par rapport à la gravité standard de la Terre modélisée comme un ellipsoïde en rotation ayant une répartition de masse homogène.
, elle prend en compte le rayon moyen de la Terre et la vitesse angulaire de la Terre à l'équateur. La sphère colorée représente ainsi les différences locales par rapport à la gravité standard de la Terre modélisée comme un ellipsoïde en rotation ayant une répartition de masse homogène.
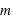 au repos à la surface de la Terre ?
au repos à la surface de la Terre ?
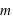 , a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
, a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
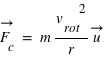 , où
, où 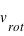 est la vitesse de rotation,
est la vitesse de rotation, 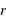 la distance entre la masse
la distance entre la masse 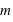 et le centre du cercle,
et le centre du cercle, 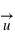 le vecteur unitaire dirigé du centre du cercle à la position de la masse.
le vecteur unitaire dirigé du centre du cercle à la position de la masse.
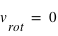 (le centre du cercle = pôle) , et à l'équateur elle est maximale (
(le centre du cercle = pôle) , et à l'équateur elle est maximale (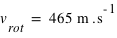 , le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
, le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
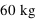 ? Quel est l'avantage de lancer un engin spatial de 300 tonnes (
? Quel est l'avantage de lancer un engin spatial de 300 tonnes (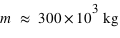 ) à proximité de l'équateur ?
) à proximité de l'équateur ?
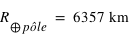 et à l'équateur
et à l'équateur 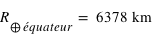 . La masse de la Terre vaut
. La masse de la Terre vaut 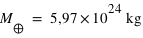 .
.
 autour d'une masse
autour d'une masse 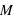 ? Est-elle dépendante de la masse du corps en mouvement ?
? Est-elle dépendante de la masse du corps en mouvement ?
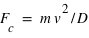 ).
).
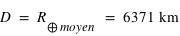 .
.
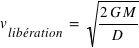 .
.
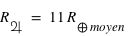 et
et 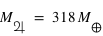 . Pour le Soleil :
. Pour le Soleil : 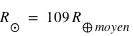 et
et 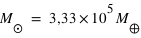 .
.
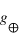 cela correspond-t-il ?
cela correspond-t-il ?
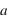 , qui fait passer un engin d'une vitesse nulle à une vitesse,
, qui fait passer un engin d'une vitesse nulle à une vitesse, 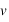 , sur une distance
, sur une distance 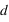 , vaut
, vaut 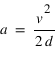 .
.
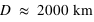 avant de les propulser plus loin pour aller explorer le système solaire ?
avant de les propulser plus loin pour aller explorer le système solaire ?
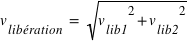 , où
, où 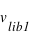 est la vitesse de libération de la Terre, et
est la vitesse de libération de la Terre, et 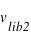 est la vitesse de libération du Soleil situé à
est la vitesse de libération du Soleil situé à 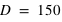 millions de kilomètres de la Terre. A cette vitesse
millions de kilomètres de la Terre. A cette vitesse 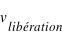 , il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil,
, il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil, 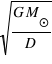 .
.
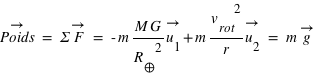 , avec
, avec 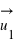 dirigé de la position de la masse
dirigé de la position de la masse 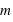 vers le centre de gravité de la Terre, et
vers le centre de gravité de la Terre, et 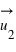 dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
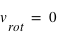 (aux pôles).
(aux pôles).
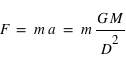 . En orbite,
. En orbite, 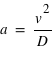 . Donc
. Donc 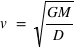 . Elle ne dépend pas de la masse du corps en orbite.
. Elle ne dépend pas de la masse du corps en orbite.
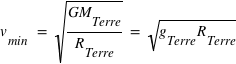 = 7,9 km.s-1.
= 7,9 km.s-1.
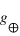 .
.
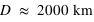 plutôt qu'à la surface de la Terre
plutôt qu'à la surface de la Terre 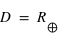 , et donc une force d'accélération,
, et donc une force d'accélération, 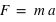 , bien moindre à fournir.
, bien moindre à fournir.
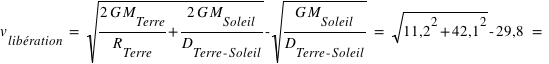 13,8 km.s-1.
13,8 km.s-1.