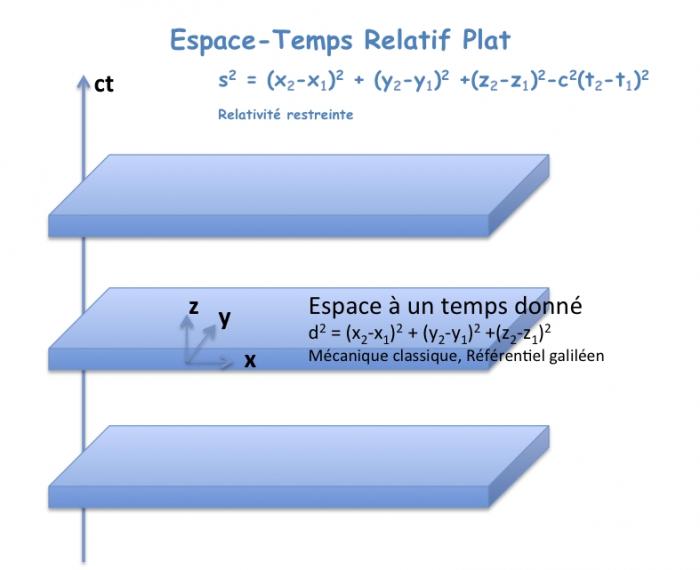
Les interactions fondamentales font intervenir la distance entre les corps matériels. Là où tout se complique, c'est que la distance n'est pas une mesure absolue...
 Seule la vitesse de la lumière est constante !
Seule la vitesse de la lumière est constante !
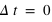 ) que dans le même référentiel (x, y, z).
) que dans le même référentiel (x, y, z).
En mécanique classique, la vitesse mesurée d'un corps matériel vaut
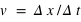 (une bille roulant dans un TGV à l'arrêt). Si ce corps matériel se déplace dans un repère en mouvement (une bille roulant dans un TGV ayant une vitesse constante,
(une bille roulant dans un TGV à l'arrêt). Si ce corps matériel se déplace dans un repère en mouvement (une bille roulant dans un TGV ayant une vitesse constante, 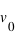 ) par rapport au lieu de mesure (le quai), alors la vitesse mesurée devient relative au repère. Elle vaut
) par rapport au lieu de mesure (le quai), alors la vitesse mesurée devient relative au repère. Elle vaut 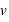 dans le repère inertiel (au repos ou avec une vitesse constante, c'est-à-dire la même dans le TGV au repos ou à vitesse constante), mais elle vaut
dans le repère inertiel (au repos ou avec une vitesse constante, c'est-à-dire la même dans le TGV au repos ou à vitesse constante), mais elle vaut 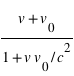 dans tout autre repère de mesure (la composition des vitesses n'est plus additive comme en mécanique classique où on aurait écrit
dans tout autre repère de mesure (la composition des vitesses n'est plus additive comme en mécanique classique où on aurait écrit 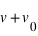 ). Cela traduit que la vitesse ne peut jamais être mesurée supérieure à la vitesse de la lumière (qui est une constante
). Cela traduit que la vitesse ne peut jamais être mesurée supérieure à la vitesse de la lumière (qui est une constante 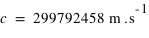 ), quelque soit le repère de mesure. Les évènements ne sont plus décrits dans une structure à trois dimensions, où leur distance
), quelque soit le repère de mesure. Les évènements ne sont plus décrits dans une structure à trois dimensions, où leur distance 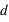 est mesurée classiquement par
est mesurée classiquement par 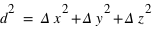 quelque soit le temps
quelque soit le temps  (espace-temps absolu), mais dans une structure à quatre dimensions, où la séparation des évènements
(espace-temps absolu), mais dans une structure à quatre dimensions, où la séparation des évènements 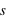 fait intervenir la distance parcourue par la lumière dans un laps de temps
fait intervenir la distance parcourue par la lumière dans un laps de temps 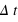 ,
, 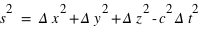 (espace-temps relativiste).
(espace-temps relativiste).
Notons que la définition du mètre est : la longueur de la distance parcourue dans le vide par la lumière pendant une durée de 1/299792458 seconde.
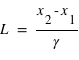 (
(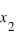 et
et 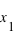 mesurés au même moment) , ou que le temps écoulé sera mesuré plus long,
mesurés au même moment) , ou que le temps écoulé sera mesuré plus long, 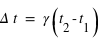 (
(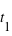 et
et 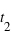 mesurés au même endroit), avec le facteur gamma (ou facteur de Lorentz) sans dimension
mesurés au même endroit), avec le facteur gamma (ou facteur de Lorentz) sans dimension 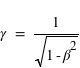 avec (
avec (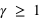 ) et
) et 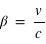 avec (
avec (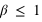 ).
).
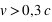 (donc pas pour un TVG...mais pour des corps matériels atteignant des vitesses relativistes telles que les particules dans des accélérateurs).
(donc pas pour un TVG...mais pour des corps matériels atteignant des vitesses relativistes telles que les particules dans des accélérateurs).
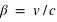
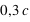
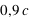
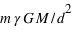 . L'accélération de la masse
. L'accélération de la masse 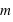 apparait plus grande dans le repère inertiel de la masse
apparait plus grande dans le repère inertiel de la masse 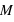 (autrement dit, le poids de la masse
(autrement dit, le poids de la masse 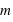 apparait plus fort) .
Nous voyons immédiatement que si un corps se déplace avec une vitesse proche de
apparait plus fort) .
Nous voyons immédiatement que si un corps se déplace avec une vitesse proche de 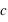 , la force sur ce corps matériel devient infinie ! Ainsi un corps matériel ayant une masse ne peut atteindre la vitesse de la lumière ; dans ce cas, la relativité est dite restreinte (
, la force sur ce corps matériel devient infinie ! Ainsi un corps matériel ayant une masse ne peut atteindre la vitesse de la lumière ; dans ce cas, la relativité est dite restreinte (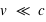 ).
).