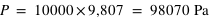Dans cette partie, nous allons aborder la force la plus commune, la gravitation, et que vous avez très probablement déjà étudiée dans votre cursus. C'est une force qui est en fait très particulière par rapport aux trois autres forces.
 Caractéristique de la matière : sa masse
Caractéristique de la matière : sa masse
Les masses sont liées entre elles via l’interaction de gravitation. L'unité de base de la masse est le kilogramme (kg).
Ses effets sont le plus familier à l’homme via la pesanteur, c’est-à-dire le poids des corps matériels. Elle provoque les marées, elle confine l’atmosphère autour de la Terre, elle maintient les planètes et les astéroïdes autour du Soleil, elle concentre le gaz, les étoiles, et la poussière des galaxies, elle forme les structures à grandes échelles de l’univers (groupes, amas, superamas)…
 Loi de conservation
Loi de conservation
La masse* est une quantité conservée dans tout phénomène de transformation de la matière.
* En fait, de part l'équivalence masse-énergie (la célèbre formule 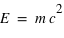 ), il est approprié de dire que c'est la masse-énergie qui est conservée.
), il est approprié de dire que c'est la masse-énergie qui est conservée.
Crédit :
ASM/Laurence Tresse
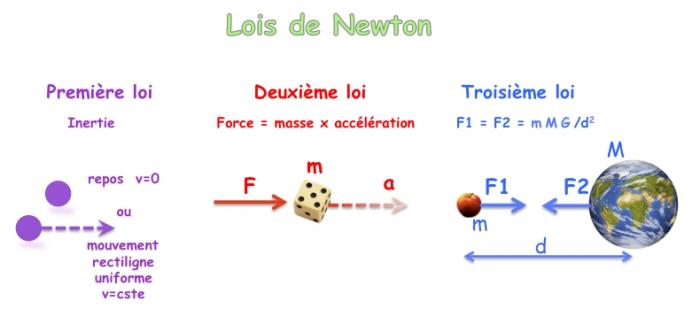
Elles forment les bases de la mécanique classique. Elles relient les forces qui agissent sur un corps matériel ayant une masse et le mouvement qui en est induit.
 Première loi de Newton ou principe de l'inertie
Première loi de Newton ou principe de l'inertie
Lex I: Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Si un corps ne subit pas de force, alors sa vitesse est constante : soit le corps est au repos (vitesse nulle) ou soit il se déplace en ligne droite avec une vitesse constante (vitesse non nulle).
 Enoncé
Enoncé
Le Principe Fondamental de la Dynamique, qui dérive de la deuxième loi de Newton, énonce que l'accélération d'un corps est la résultante des forces qu'il subit : 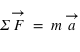 .
.
 Appplication
Appplication
Dans l'exercice précédent, nous avons négligé le fait que la Terre est légèrement aplatie au niveau des pôles, et la rotation autour de son axe, sans compter qu'elle est aussi une sphère avec un relief très varié... Etudions dans le prochain exercice leur prise en compte, en appliquant le principe fondamental de la dynamique, afin de mesurer localement la pesanteur terrestre.
Les variations locales de la pesanteur terrestre

La variation locale du champ de pesanteur terrestre illustré avec les données datant de juillet 2003 de la mission spatiale GRACE - du bleu foncé (le plus faible) au rouge foncé (le plus fort). La gravité standard à la surface de la Terre vaut, par convention,
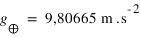
, elle prend en compte le rayon moyen de la Terre et la vitesse angulaire de la Terre à l'équateur. La sphère colorée représente ainsi les différences locales par rapport à la gravité standard de la Terre modélisée comme un ellipsoïde en rotation ayant une répartition de masse homogène.
Crédit :
University of Texas Center for Space Research and NASA
 Se libérer de la pesanteur...
Se libérer de la pesanteur...
Difficulté : ☆☆☆
Pour se libérer totalement de la pesanteur, la vitesse doit être au moins égale à : 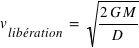 .
.
Question 1)
Combien vaut la vitesse de libération pour la Terre, Jupiter et le Soleil ?
Question 2)
Dans le cas d'un décollage vertical, quelle serait l'accélération (constante et linéaire) nécessaire pour faire passer un engin d'une vitesse nulle à la vitesse de libération terrestre (cf. question 1) sur une distance de 1000 km ? A combien de 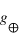 cela correspond-t-il ?
cela correspond-t-il ?
Question 3)
Pourquoi place-t-on les sondes spatiales d'abord en orbite basse 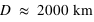 avant de les propulser plus loin pour aller explorer le système solaire ?
avant de les propulser plus loin pour aller explorer le système solaire ?
Question 4)
Quelle est l'expression de la vitesse de libération de l'influence gravitationnelle du Soleil à partir de la surface de la Terre ? Combien vaut-elle ?
 Définition
Définition
La pression, 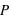 , est la force,
, est la force, 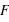 , rapportée à la surface,
, rapportée à la surface, 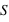 , sur laquelle elle s'applique,
, sur laquelle elle s'applique, 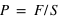 . Dans le système d'unités SI, un pascal (Pa) correspond à une force de
. Dans le système d'unités SI, un pascal (Pa) correspond à une force de 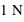 appliquée sur une surface de
appliquée sur une surface de 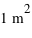 , et, est donc homogène à l'unité de base kg.m-1.s-2.
, et, est donc homogène à l'unité de base kg.m-1.s-2.
 La pression atmosphérique
La pression atmosphérique
L'atmosphère terrestre confinée par la force de gravité
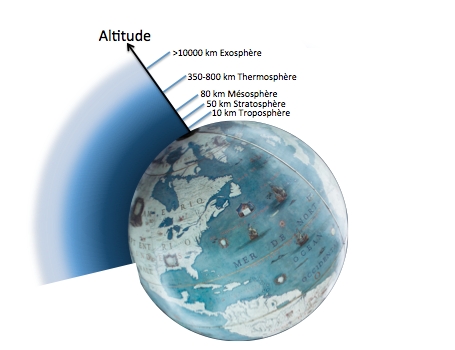
L'atmosphère terrestre est une couche de matière gazeuse confinée par la gravité de la Terre. Sa densité devient plus faible avec l'augmentation de l'altitude. Bien qu'il n'y ait pas une limite précise entre l'atmosphère et l'espace, en aéronautique ses effets sont considérés en dessous de 100 km d'altitude (dit aussi la ligne de Kármán). La navette spatiale internationale (ISS) est en orbite à une altitude d'environ 400 km, le Télescope Spatial Hubble (HST) l'est à 590 km ; ils orbitent dans la thermosphère.
Crédit :
ASM/Laurence Tresse (Globe terrestre de Coronelli, BnF)
 La sphère de Hill ou de Roche
La sphère de Hill ou de Roche
Difficulté : ☆
Question 1)
Calculer le rayon de la sphère de Hill de la Terre dans le champ de gravité du Soleil. Qu'en déduisez-vous pour la Lune ? pour la planète la plus proche Mars ?
On négligera l'influence des autres planètes et on exprimera le rayon en Unité Astronomique avec 1 U.A. = distance Terre-Soleil. On utilisera pour la Terre, 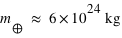 et pour le Soleil,
et pour le Soleil, 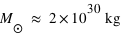 . La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.
. La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.
Question 2)
L'influence gravitationnelle du système solaire est estimée à 125000 U.A. Qu'en déduisez-vous pour l'étoile la plus proche du système solaire, Proxima du Centaure, située à 270000 U.A. environ ?
Les interactions fondamentales font intervenir la distance entre les corps matériels. Là où tout se complique, c'est que la distance n'est pas une mesure absolue...
 Seule la vitesse de la lumière est constante !
Seule la vitesse de la lumière est constante !
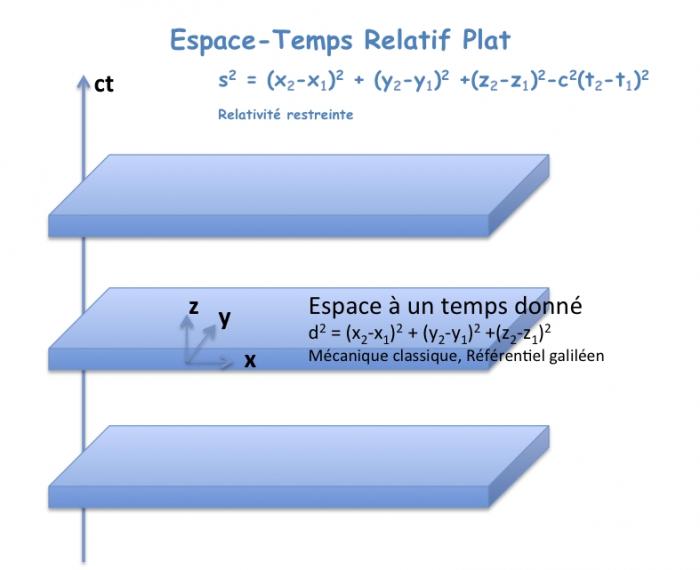
En mécanique classique, un évènement est décrit dans une structure à 3 dimensions. En relativité, il est décrit dans une structure à 4 dimensions. Cette quatrième dimension implique que nous ne pouvons mesurer des évènements simultanés (
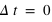
) que dans le même référentiel (x, y, z).
Crédit :
ASM/Laurence Tresse
En mécanique classique, la vitesse mesurée d'un corps matériel vaut
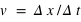 (une bille roulant dans un TGV à l'arrêt). Si ce corps matériel se déplace dans un repère en mouvement (une bille roulant dans un TGV ayant une vitesse constante,
(une bille roulant dans un TGV à l'arrêt). Si ce corps matériel se déplace dans un repère en mouvement (une bille roulant dans un TGV ayant une vitesse constante, 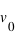 ) par rapport au lieu de mesure (le quai), alors la vitesse mesurée devient relative au repère. Elle vaut
) par rapport au lieu de mesure (le quai), alors la vitesse mesurée devient relative au repère. Elle vaut 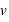 dans le repère inertiel (au repos ou avec une vitesse constante, c'est-à-dire la même dans le TGV au repos ou à vitesse constante), mais elle vaut
dans le repère inertiel (au repos ou avec une vitesse constante, c'est-à-dire la même dans le TGV au repos ou à vitesse constante), mais elle vaut 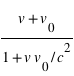 dans tout autre repère de mesure (la composition des vitesses n'est plus additive comme en mécanique classique où on aurait écrit
dans tout autre repère de mesure (la composition des vitesses n'est plus additive comme en mécanique classique où on aurait écrit 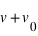 ). Cela traduit que la vitesse ne peut jamais être mesurée supérieure à la vitesse de la lumière (qui est une constante
). Cela traduit que la vitesse ne peut jamais être mesurée supérieure à la vitesse de la lumière (qui est une constante 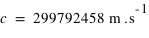 ), quelque soit le repère de mesure. Les évènements ne sont plus décrits dans une structure à trois dimensions, où leur distance
), quelque soit le repère de mesure. Les évènements ne sont plus décrits dans une structure à trois dimensions, où leur distance 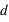 est mesurée classiquement par
est mesurée classiquement par 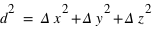 quelque soit le temps
quelque soit le temps  (espace-temps absolu), mais dans une structure à quatre dimensions, où la séparation des évènements
(espace-temps absolu), mais dans une structure à quatre dimensions, où la séparation des évènements 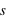 fait intervenir la distance parcourue par la lumière dans un laps de temps
fait intervenir la distance parcourue par la lumière dans un laps de temps 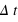 ,
, 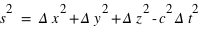 (espace-temps relativiste).
(espace-temps relativiste).
Notons que la définition du mètre est : la longueur de la distance parcourue dans le vide par la lumière pendant une durée de 1/299792458 seconde.
 Quelle vitesse pour des effets relativistes perceptibles ?
Quelle vitesse pour des effets relativistes perceptibles ?
Les effets relativistes deviennent perceptibles pour 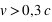 (donc pas pour un TVG...mais pour des corps matériels atteignant des vitesses relativistes telles que les particules dans des accélérateurs).
(donc pas pour un TVG...mais pour des corps matériels atteignant des vitesses relativistes telles que les particules dans des accélérateurs).
| Vitesse (km.h-1) | 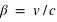 | Facteur γ | Longueur mesurée (1 m) | Temps écoulé (1 s) |
|---|
| 574,8 vitesse record du TGV | 0,0000005
| 1,00000000000004 | 0,99999999999996
| 1,00000000000004 |
| 27700 vitesse de la station spatiale internationale | 0,00003 | 1,0000000003
| 0,9999999997 | 1,0000000003
|
| 252800 vitesse de la sonde Helios (objet le plus rapide fait par l'humain) | 0,0002
| 1,00000003 | 0,99999997
| 1,00000003 |
| 1990000 vitesse de la Voie Lactée | 0,02 | 1,000002
| 0,999998
| 1,000002
|
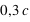 | 0,3 | 1,05 | 0,95 | 1,05 |
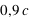 | 0,9 | 2,3 | 0,4 | 2,3 |
 La présence d'une masse courbe l'espace-temps !
La présence d'une masse courbe l'espace-temps !
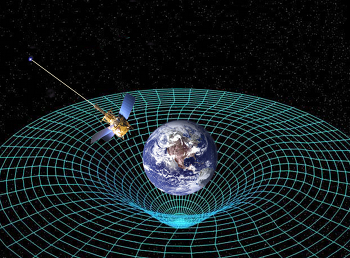
L'espace-temps courbé par la présence d'une masse telle que la Terre.
Crédit :
NASA
La vraie nature physique de la force gravitationnelle est en fait bien plus complexe. Nous verrons plus loin que cette théorie a été englobée dans une théorie plus large, la relativité générale qui s’applique à de la matière ayant une vitesse proche ou égale à la vitesse 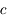 (la lumière est alors déviée au passage d’un corps massif voire absorbée par un objet extrêmement massif comme un trou noir). En fait, une masse déforme l’espace-temps en le courbant (courbure de
(la lumière est alors déviée au passage d’un corps massif voire absorbée par un objet extrêmement massif comme un trou noir). En fait, une masse déforme l’espace-temps en le courbant (courbure de 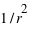 ), ce n’est plus un espace-temps plat comme en relativité restreinte mais un espace-temps courbé par la présence de corps massifs. Un autre corps matériel (avec une masse plus faible ou sans masse) va suivre cet espace-temps déformé. On peut imager cet effet comme une bille d’acier que l'on pose sur un drap plat ; elle creuse le drap, à son voisinage une autre bille moins massive tombera en tournoyant dans ce creux formé. Si ce drap est invisible, on a l’impression d’une attraction entre les deux billes, qui est en fait une fausse impression, car ce ne sont pas les corps qui s’attirent, mais c’est la masse d’un corps matériel qui déforme la structure espace-temps (le drap), déformation qui sera subie inéluctablement par tout autre corps matériel (moins massif ou sans masse). L’un et l’autre effet ne sont pas distinguables.
), ce n’est plus un espace-temps plat comme en relativité restreinte mais un espace-temps courbé par la présence de corps massifs. Un autre corps matériel (avec une masse plus faible ou sans masse) va suivre cet espace-temps déformé. On peut imager cet effet comme une bille d’acier que l'on pose sur un drap plat ; elle creuse le drap, à son voisinage une autre bille moins massive tombera en tournoyant dans ce creux formé. Si ce drap est invisible, on a l’impression d’une attraction entre les deux billes, qui est en fait une fausse impression, car ce ne sont pas les corps qui s’attirent, mais c’est la masse d’un corps matériel qui déforme la structure espace-temps (le drap), déformation qui sera subie inéluctablement par tout autre corps matériel (moins massif ou sans masse). L’un et l’autre effet ne sont pas distinguables.
 En relativité générale, la gravitation n’est pas une force d’interaction entre deux corps...
En relativité générale, la gravitation n’est pas une force d’interaction entre deux corps...
Elle est la manifestation d’un espace courbé par la présence de corps massifs.
La théorie de la relativité générale s'applique principalement lorsque le potentiel de gravité est fort,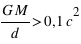 . Pour terminer, elle est vérifiée expérimentalement, mais pas sur des échelles extrêmement petites (échelles quantiques), où d’autres forces d’interaction dominent les phénomènes physiques.
. Pour terminer, elle est vérifiée expérimentalement, mais pas sur des échelles extrêmement petites (échelles quantiques), où d’autres forces d’interaction dominent les phénomènes physiques.
 Lieux privilégiés de la gravité relativiste
Lieux privilégiés de la gravité relativiste
Difficulté : ☆
Le potentiel de gravitation rapporté à 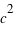 est dit fort lorsque
est dit fort lorsque 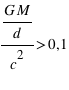 . Dans ce cas, les effets de la relativité générale sont perceptibles.
. Dans ce cas, les effets de la relativité générale sont perceptibles.
Question 1)
Calculer l'ordre de grandeur du potentiel de gravité rapporté à 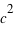 à la surface de la Terre, du Soleil, d'une étoile à neutrons et d'un trou noir. Qu'en déduisez-vous ?
à la surface de la Terre, du Soleil, d'une étoile à neutrons et d'un trou noir. Qu'en déduisez-vous ?
- Question 1
Aide :
La masse de la Terre vaut 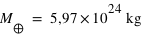 et son rayon moyen vaut
et son rayon moyen vaut 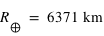 .
.
Solution :
A la surface de la Terre, 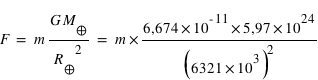 = m (kg) x 9,82 (m3.kg-1.s-2). Pour la pomme,
= m (kg) x 9,82 (m3.kg-1.s-2). Pour la pomme, 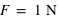 , et pour la personne,
, et pour la personne, 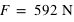 .
.
- Question 2
Solution :
La force d'interaction de la Terre sur la pomme est égale à celle de la pomme sur la Terre, F(pomme→Terre) = F(Terre→pomme) [cela correspond à la troisième loi de Newton], donc dans ce cas, 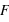 vaut également 1 N.
vaut également 1 N.
- Question 3
Solution :
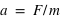 . L'accélération due à la masse de la Terre vaut pour la pomme,
. L'accélération due à la masse de la Terre vaut pour la pomme, 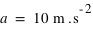 , et pour la personne,
, et pour la personne, 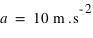 . Quelle que soit la masse considérée, l'accélération des corps matériels due à la force de gravité est la même, c'est la conséquence de la deuxième loi de Newton.
. Quelle que soit la masse considérée, l'accélération des corps matériels due à la force de gravité est la même, c'est la conséquence de la deuxième loi de Newton.
- Question 4
Solution :
L'accélération de la Terre due à la masse de la pomme vaut, 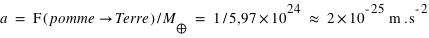 , due à la personne,
, due à la personne, 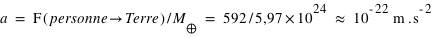 . L'accélération à laquelle est soumise la Terre due à la masse de la pomme ou de la personne est totalement négligeable devant celle produite par la Terre ! Plus la masse d'un corps est importante, plus son accélération est forte et domine. La force de gravitation est dite cumulative.
. L'accélération à laquelle est soumise la Terre due à la masse de la pomme ou de la personne est totalement négligeable devant celle produite par la Terre ! Plus la masse d'un corps est importante, plus son accélération est forte et domine. La force de gravitation est dite cumulative.
- Question 5
Solution :
Une force contraire et égale à la force de pesanteur doit exister. C'est la force normale. On l'apelle aussi force de soutien, force de contact, force de résistance de surface, voire force de réaction du plan. Cette force n'est pas due à l'interaction entre des masses, mais à la répulsion électrique des molécules de surface des deux objets comme nous le verrons lors de l'introduction de la deuxième force fondamentale.
- Question 1
Aide :
Lorsqu'un corps matériel, de masse 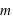 , a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
, a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
La force centrifuge dans le cas d'un mouvement circulaire uniforme vaut 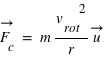 , où
, où 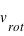 est la vitesse de rotation,
est la vitesse de rotation, 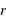 la distance entre la masse
la distance entre la masse 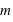 et le centre du cercle,
et le centre du cercle, 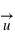 le vecteur unitaire dirigé du centre du cercle à la position de la masse.
le vecteur unitaire dirigé du centre du cercle à la position de la masse.
Pour le cas d'un corps matériel à la surface terrestre, noter bien que c'est le centre du cercle (qui se situe le long de l'axe de rotation terrestre), et non le centre de la sphère terrestre. Donc, aux pôles cette force est nulle : 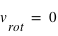 (le centre du cercle = pôle) , et à l'équateur elle est maximale (
(le centre du cercle = pôle) , et à l'équateur elle est maximale (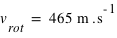 , le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
, le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
Solution :
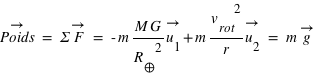 , avec
, avec 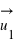 dirigé de la position de la masse
dirigé de la position de la masse 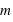 vers le centre de gravité de la Terre, et
vers le centre de gravité de la Terre, et 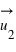 dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
- Question 2
Solution :
Non, sauf lorsque 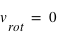 (aux pôles).
(aux pôles).
- Question 3
Aide :
Le rayon terrestre aux pôles vaut 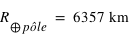 et à l'équateur
et à l'équateur 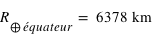 . La masse de la Terre vaut
. La masse de la Terre vaut 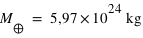 .
.
Solution :
Aux pôles, F = 60 x 6,674 x 10-11 x 5,97 1024/ 63570002 = 60 x 9,86 = 592 N, à l'équateur, F = 60 x 6,674 x 10-11 x 5,97 1024 / 63780002 - 60 x 4652/6378000 = 60 x 9,79 - 60 x 0,03 = 60 x 9,76 = 586 N. Une différence de 6 N parait négligeable, mais pour un objet de masse bien plus importante, telle une fusée, de plusieurs tonnes la différence signifie bien moins d'énergie à fournir au décollage, soit pour 300 tonnes, la différence de pesanteur est de l'ordre de ~ 30 000 N ! A proximité de l'équateur, la force à fournir est donc la plus faible ; c'est le cas du centre spatial de Kourou en Guyane.
- Question 4
Solution :
La force centrifuge l'emporterait sur la force de gravitation, les habitants aux alentours de l'équateur seraient expulsés de la Terre !
- Question 1
Aide :
Pour Jupiter : 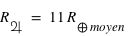 et
et 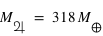 . Pour le Soleil :
. Pour le Soleil : 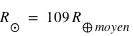 et
et 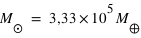 .
.
Solution :
Pour la Terre, Jupiter et le Soleil, vlibération = 11,2 km.s-1, 59 km.s-1 et 618 km.s-1, respectivement.
- Question 2
Aide :
L'accélération constante et linéaire, 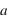 , qui fait passer un engin d'une vitesse nulle à une vitesse,
, qui fait passer un engin d'une vitesse nulle à une vitesse, 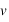 , sur une distance
, sur une distance 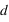 , vaut
, vaut 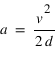 .
.
Solution :
v = 11,2 km.s-1 donc a = 11,22/ 2 x 1000 = 0,06272 km.s-2, soit ~63 m.s-2, soit ~6 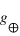 .
.
- Question 3
Solution :
Lorsqu'on met d'abord en orbite une sonde spatiale, on bénéficie du fait que la vitesse de libération est moindre à l'altitude 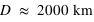 plutôt qu'à la surface de la Terre
plutôt qu'à la surface de la Terre 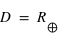 , et donc une force d'accélération,
, et donc une force d'accélération, 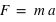 , bien moindre à fournir.
, bien moindre à fournir.
- Question 4
Aide :
On négligera l'influence des autres planètes. Les vitesses s'ajoutant au carré, soit 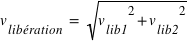 , où
, où 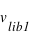 est la vitesse de libération de la Terre, et
est la vitesse de libération de la Terre, et 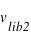 est la vitesse de libération du Soleil situé à
est la vitesse de libération du Soleil situé à 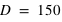 millions de kilomètres de la Terre. A cette vitesse
millions de kilomètres de la Terre. A cette vitesse 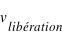 , il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil,
, il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil, 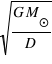 .
.
Solution :
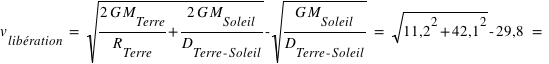 13,8 km.s-1.
13,8 km.s-1.
 Caractéristique de la matière : sa masse
Caractéristique de la matière : sa masse Loi de conservation
Loi de conservation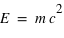 ), il est approprié de dire que c'est la masse-énergie qui est conservée.
), il est approprié de dire que c'est la masse-énergie qui est conservée.
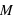 , crée un champ de gravité autour de lui dans une sphère de rayon
, crée un champ de gravité autour de lui dans une sphère de rayon 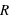 ,
, 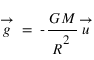 .
. 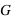 est la constante de gravitation dont la mesure vaut
est la constante de gravitation dont la mesure vaut 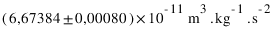 , et
, et 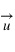 le vecteur unitaire partant de la masse
le vecteur unitaire partant de la masse 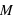 . Dans ce champ, tout autre corps de matière va subir cette attraction gravitationnelle. La force d’interaction subie par une masse
. Dans ce champ, tout autre corps de matière va subir cette attraction gravitationnelle. La force d’interaction subie par une masse 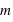 située à une distance
située à une distance 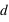 de la masse
de la masse 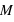 vaut :
vaut : 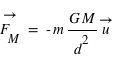 .
.
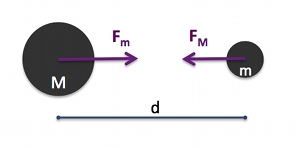
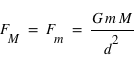 . Elle agit à toutes les distances. Si
. Elle agit à toutes les distances. Si 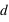 diminue d'un facteur 10, la force augmente d'un facteur 100.
diminue d'un facteur 10, la force augmente d'un facteur 100.
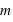 subit l’accélération
subit l’accélération 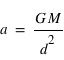 . Ceci a pour conséquence l’égalité de la masse grave (ou pesante, soit de la masse
. Ceci a pour conséquence l’égalité de la masse grave (ou pesante, soit de la masse 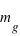 qui subit la gravité
qui subit la gravité 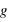 ), et de la masse inerte (soit de la masse
), et de la masse inerte (soit de la masse 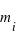 ayant un mouvement uniformément accéléré
ayant un mouvement uniformément accéléré 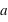 ),
), 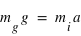 . Dans les faits expérimentaux, elle sont vérifiées égales à
. Dans les faits expérimentaux, elle sont vérifiées égales à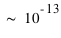 près (prévu pour un lancement en 2015, le satellite français Microscope devrait permettre une précision 100 fois meilleure, soit à
près (prévu pour un lancement en 2015, le satellite français Microscope devrait permettre une précision 100 fois meilleure, soit à 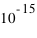 près).
près).

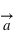 d'un corps est parallèle et directement proportionelle à la force nette appliquée
d'un corps est parallèle et directement proportionelle à la force nette appliquée 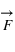 sur le corps, elle est dans la même direction que la force nette, et elle est inversement proportionnelle à la masse
sur le corps, elle est dans la même direction que la force nette, et elle est inversement proportionnelle à la masse 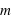 du corps, soit
du corps, soit 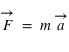 .
.
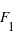 sur un deuxième corps, le deuxième corps exerce simultanément une force
sur un deuxième corps, le deuxième corps exerce simultanément une force 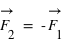 sur le premier corps. Ainsi
sur le premier corps. Ainsi 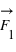 et
et 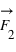 sont égales et opposées en direction.
sont égales et opposées en direction.
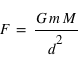 , sachant que la constante de gravitation,
, sachant que la constante de gravitation, 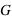 , est exprimée
, est exprimée 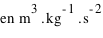 ?
?
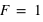 Newton (N) à quoi correspond un Newton dans le système SI, et quelle est sa signification ?
Newton (N) à quoi correspond un Newton dans le système SI, et quelle est sa signification ?
 par seconde d’un corps matériel ayant une masse de
par seconde d’un corps matériel ayant une masse de 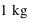 ?
?
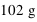 , et par une personne ayant une masse corporelle de
, et par une personne ayant une masse corporelle de 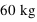 ?
?
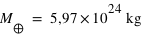 et son rayon moyen vaut
et son rayon moyen vaut 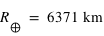 .
.
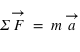 .
.

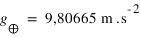 , elle prend en compte le rayon moyen de la Terre et la vitesse angulaire de la Terre à l'équateur. La sphère colorée représente ainsi les différences locales par rapport à la gravité standard de la Terre modélisée comme un ellipsoïde en rotation ayant une répartition de masse homogène.
, elle prend en compte le rayon moyen de la Terre et la vitesse angulaire de la Terre à l'équateur. La sphère colorée représente ainsi les différences locales par rapport à la gravité standard de la Terre modélisée comme un ellipsoïde en rotation ayant une répartition de masse homogène.
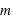 au repos à la surface de la Terre ?
au repos à la surface de la Terre ?
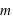 , a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
, a un mouvement circulaire autour de la masse attirante, il subit une force centrifuge (comme celle ressentie dans une voiture dans un virage) en sus de la force d'interaction des masses. La rotation de la Terre implique qu'un corps matériel à sa surface possède un mouvement circulaire autour de l'axe de rotation terrestre (appelé aussi l'axe Nord-Sud ou l'axe des pôles).
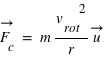 , où
, où 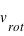 est la vitesse de rotation,
est la vitesse de rotation, 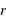 la distance entre la masse
la distance entre la masse 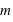 et le centre du cercle,
et le centre du cercle, 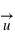 le vecteur unitaire dirigé du centre du cercle à la position de la masse.
le vecteur unitaire dirigé du centre du cercle à la position de la masse.
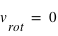 (le centre du cercle = pôle) , et à l'équateur elle est maximale (
(le centre du cercle = pôle) , et à l'équateur elle est maximale (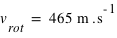 , le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
, le centre du cercle = centre de gravité de la Terre), et elle varie du pôle à l'équateur selon la latitude du lieu.
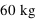 ? Quel est l'avantage de lancer un engin spatial de 300 tonnes (
? Quel est l'avantage de lancer un engin spatial de 300 tonnes (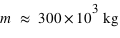 ) à proximité de l'équateur ?
) à proximité de l'équateur ?
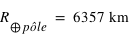 et à l'équateur
et à l'équateur 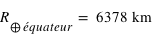 . La masse de la Terre vaut
. La masse de la Terre vaut 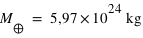 .
.
 autour d'une masse
autour d'une masse 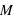 ? Est-elle dépendante de la masse du corps en mouvement ?
? Est-elle dépendante de la masse du corps en mouvement ?
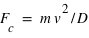 ).
).
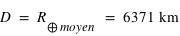 .
.
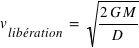 .
.
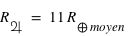 et
et 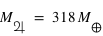 . Pour le Soleil :
. Pour le Soleil : 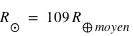 et
et 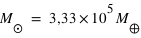 .
.
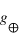 cela correspond-t-il ?
cela correspond-t-il ?
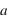 , qui fait passer un engin d'une vitesse nulle à une vitesse,
, qui fait passer un engin d'une vitesse nulle à une vitesse, 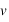 , sur une distance
, sur une distance 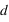 , vaut
, vaut 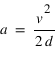 .
.
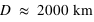 avant de les propulser plus loin pour aller explorer le système solaire ?
avant de les propulser plus loin pour aller explorer le système solaire ?
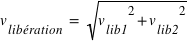 , où
, où 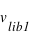 est la vitesse de libération de la Terre, et
est la vitesse de libération de la Terre, et 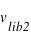 est la vitesse de libération du Soleil situé à
est la vitesse de libération du Soleil situé à 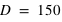 millions de kilomètres de la Terre. A cette vitesse
millions de kilomètres de la Terre. A cette vitesse 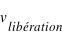 , il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil,
, il faudra aussi soustraire la vitesse liée au fait que la Terre est en orbite autour du Soleil, 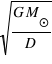 .
.
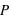 , est la force,
, est la force, 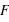 , rapportée à la surface,
, rapportée à la surface, 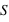 , sur laquelle elle s'applique,
, sur laquelle elle s'applique, 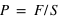 . Dans le système d'unités SI, un pascal (Pa) correspond à une force de
. Dans le système d'unités SI, un pascal (Pa) correspond à une force de 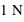 appliquée sur une surface de
appliquée sur une surface de 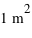 , et, est donc homogène à l'unité de base kg.m-1.s-2.
, et, est donc homogène à l'unité de base kg.m-1.s-2.

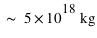 . Sachant que la superficie du globe terrestre vaut
. Sachant que la superficie du globe terrestre vaut 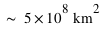 , combien vaut la masse moyenne au-dessus d'un mètre carré ?
, combien vaut la masse moyenne au-dessus d'un mètre carré ?
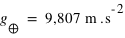 ), à quelle pression atmosphérique cela correspond-t-il ?
), à quelle pression atmosphérique cela correspond-t-il ?
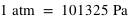 (valeur standard officielle). A votre avis pourquoi votre résultat précédent diffère de cette valeur ?
(valeur standard officielle). A votre avis pourquoi votre résultat précédent diffère de cette valeur ?
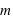 à une distance
à une distance 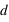 d'un corps plus massif de masse
d'un corps plus massif de masse 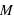 , le rayon de sa sphère de Hill vaut
, le rayon de sa sphère de Hill vaut ![r_H=d\, \sqrt[3]{\frac{m}{3M}}](../pages_forces/equations_force-gravitation-exercices-autre/equation17.png) .
.
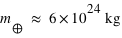 et pour le Soleil,
et pour le Soleil, 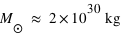 . La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.
. La Lune se situe à 0,0026 U.A. environ de la Terre. Mars atteint une distance minimale de la Terre à 0,37 U.A.

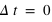 ) que dans le même référentiel (x, y, z).
) que dans le même référentiel (x, y, z).
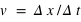 (une bille roulant dans un TGV à l'arrêt). Si ce corps matériel se déplace dans un repère en mouvement (une bille roulant dans un TGV ayant une vitesse constante,
(une bille roulant dans un TGV à l'arrêt). Si ce corps matériel se déplace dans un repère en mouvement (une bille roulant dans un TGV ayant une vitesse constante, 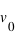 ) par rapport au lieu de mesure (le quai), alors la vitesse mesurée devient relative au repère. Elle vaut
) par rapport au lieu de mesure (le quai), alors la vitesse mesurée devient relative au repère. Elle vaut 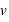 dans le repère inertiel (au repos ou avec une vitesse constante, c'est-à-dire la même dans le TGV au repos ou à vitesse constante), mais elle vaut
dans le repère inertiel (au repos ou avec une vitesse constante, c'est-à-dire la même dans le TGV au repos ou à vitesse constante), mais elle vaut 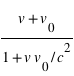 dans tout autre repère de mesure (la composition des vitesses n'est plus additive comme en mécanique classique où on aurait écrit
dans tout autre repère de mesure (la composition des vitesses n'est plus additive comme en mécanique classique où on aurait écrit 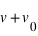 ). Cela traduit que la vitesse ne peut jamais être mesurée supérieure à la vitesse de la lumière (qui est une constante
). Cela traduit que la vitesse ne peut jamais être mesurée supérieure à la vitesse de la lumière (qui est une constante 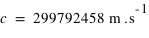 ), quelque soit le repère de mesure. Les évènements ne sont plus décrits dans une structure à trois dimensions, où leur distance
), quelque soit le repère de mesure. Les évènements ne sont plus décrits dans une structure à trois dimensions, où leur distance 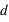 est mesurée classiquement par
est mesurée classiquement par 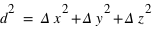 quelque soit le temps
quelque soit le temps  (espace-temps absolu), mais dans une structure à quatre dimensions, où la séparation des évènements
(espace-temps absolu), mais dans une structure à quatre dimensions, où la séparation des évènements 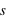 fait intervenir la distance parcourue par la lumière dans un laps de temps
fait intervenir la distance parcourue par la lumière dans un laps de temps 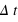 ,
, 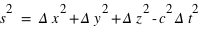 (espace-temps relativiste).
(espace-temps relativiste).
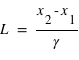 (
(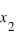 et
et 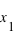 mesurés au même moment) , ou que le temps écoulé sera mesuré plus long,
mesurés au même moment) , ou que le temps écoulé sera mesuré plus long, 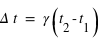 (
(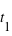 et
et 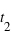 mesurés au même endroit), avec le facteur gamma (ou facteur de Lorentz) sans dimension
mesurés au même endroit), avec le facteur gamma (ou facteur de Lorentz) sans dimension 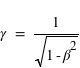 avec (
avec (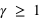 ) et
) et 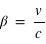 avec (
avec (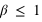 ).
).
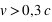 (donc pas pour un TVG...mais pour des corps matériels atteignant des vitesses relativistes telles que les particules dans des accélérateurs).
(donc pas pour un TVG...mais pour des corps matériels atteignant des vitesses relativistes telles que les particules dans des accélérateurs).
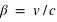
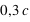
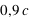
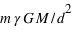 . L'accélération de la masse
. L'accélération de la masse 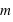 apparait plus grande dans le repère inertiel de la masse
apparait plus grande dans le repère inertiel de la masse 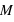 (autrement dit, le poids de la masse
(autrement dit, le poids de la masse 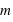 apparait plus fort) .
Nous voyons immédiatement que si un corps se déplace avec une vitesse proche de
apparait plus fort) .
Nous voyons immédiatement que si un corps se déplace avec une vitesse proche de 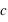 , la force sur ce corps matériel devient infinie ! Ainsi un corps matériel ayant une masse ne peut atteindre la vitesse de la lumière ; dans ce cas, la relativité est dite restreinte (
, la force sur ce corps matériel devient infinie ! Ainsi un corps matériel ayant une masse ne peut atteindre la vitesse de la lumière ; dans ce cas, la relativité est dite restreinte (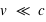 ).
).

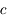 (la lumière est alors déviée au passage d’un corps massif voire absorbée par un objet extrêmement massif comme un trou noir). En fait, une masse déforme l’espace-temps en le courbant (courbure de
(la lumière est alors déviée au passage d’un corps massif voire absorbée par un objet extrêmement massif comme un trou noir). En fait, une masse déforme l’espace-temps en le courbant (courbure de 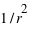 ), ce n’est plus un espace-temps plat comme en relativité restreinte mais un espace-temps courbé par la présence de corps massifs. Un autre corps matériel (avec une masse plus faible ou sans masse) va suivre cet espace-temps déformé. On peut imager cet effet comme une bille d’acier que l'on pose sur un drap plat ; elle creuse le drap, à son voisinage une autre bille moins massive tombera en tournoyant dans ce creux formé. Si ce drap est invisible, on a l’impression d’une attraction entre les deux billes, qui est en fait une fausse impression, car ce ne sont pas les corps qui s’attirent, mais c’est la masse d’un corps matériel qui déforme la structure espace-temps (le drap), déformation qui sera subie inéluctablement par tout autre corps matériel (moins massif ou sans masse). L’un et l’autre effet ne sont pas distinguables.
), ce n’est plus un espace-temps plat comme en relativité restreinte mais un espace-temps courbé par la présence de corps massifs. Un autre corps matériel (avec une masse plus faible ou sans masse) va suivre cet espace-temps déformé. On peut imager cet effet comme une bille d’acier que l'on pose sur un drap plat ; elle creuse le drap, à son voisinage une autre bille moins massive tombera en tournoyant dans ce creux formé. Si ce drap est invisible, on a l’impression d’une attraction entre les deux billes, qui est en fait une fausse impression, car ce ne sont pas les corps qui s’attirent, mais c’est la masse d’un corps matériel qui déforme la structure espace-temps (le drap), déformation qui sera subie inéluctablement par tout autre corps matériel (moins massif ou sans masse). L’un et l’autre effet ne sont pas distinguables.
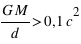 . Pour terminer, elle est vérifiée expérimentalement, mais pas sur des échelles extrêmement petites (échelles quantiques), où d’autres forces d’interaction dominent les phénomènes physiques.
. Pour terminer, elle est vérifiée expérimentalement, mais pas sur des échelles extrêmement petites (échelles quantiques), où d’autres forces d’interaction dominent les phénomènes physiques.
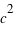 est dit fort lorsque
est dit fort lorsque 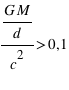 . Dans ce cas, les effets de la relativité générale sont perceptibles.
. Dans ce cas, les effets de la relativité générale sont perceptibles.
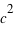 à la surface de la Terre, du Soleil, d'une étoile à neutrons et d'un trou noir. Qu'en déduisez-vous ?
à la surface de la Terre, du Soleil, d'une étoile à neutrons et d'un trou noir. Qu'en déduisez-vous ?
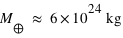 et
et 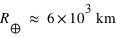 ;
; 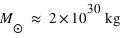 et
et 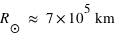 ;
; 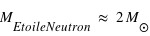 et
et  ; et pour un trou noir de masse intermédiaire
; et pour un trou noir de masse intermédiaire 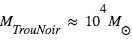 et
et 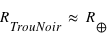 .
.
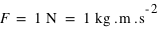 . Une force de 1 Newton est la force capable de fournir une accélération de
. Une force de 1 Newton est la force capable de fournir une accélération de 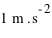 à un corps d'une masse de
à un corps d'une masse de 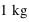 . Cela correspond à la deuxième loi de Newton,
. Cela correspond à la deuxième loi de Newton, 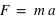 .
.
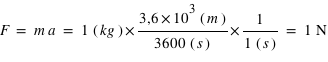
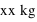 à la question du poids, alors que cela correspond à la masse corporelle. Le poids est une force, et il doit être exprimé en Newton. Le poids est la force qui fournit une accélération à une masse, c'est la force dite aussi de pesanteur.
à la question du poids, alors que cela correspond à la masse corporelle. Le poids est une force, et il doit être exprimé en Newton. Le poids est la force qui fournit une accélération à une masse, c'est la force dite aussi de pesanteur.
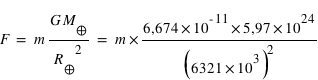 = m (kg) x 9,82 (m3.kg-1.s-2). Pour la pomme,
= m (kg) x 9,82 (m3.kg-1.s-2). Pour la pomme, 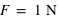 , et pour la personne,
, et pour la personne, 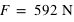 .
.
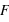 vaut également 1 N.
vaut également 1 N.
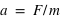 . L'accélération due à la masse de la Terre vaut pour la pomme,
. L'accélération due à la masse de la Terre vaut pour la pomme, 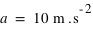 , et pour la personne,
, et pour la personne, 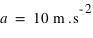 . Quelle que soit la masse considérée, l'accélération des corps matériels due à la force de gravité est la même, c'est la conséquence de la deuxième loi de Newton.
. Quelle que soit la masse considérée, l'accélération des corps matériels due à la force de gravité est la même, c'est la conséquence de la deuxième loi de Newton.
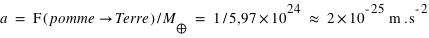 , due à la personne,
, due à la personne, 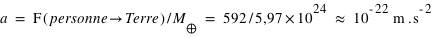 . L'accélération à laquelle est soumise la Terre due à la masse de la pomme ou de la personne est totalement négligeable devant celle produite par la Terre ! Plus la masse d'un corps est importante, plus son accélération est forte et domine. La force de gravitation est dite cumulative.
. L'accélération à laquelle est soumise la Terre due à la masse de la pomme ou de la personne est totalement négligeable devant celle produite par la Terre ! Plus la masse d'un corps est importante, plus son accélération est forte et domine. La force de gravitation est dite cumulative.
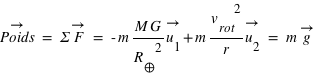 , avec
, avec 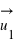 dirigé de la position de la masse
dirigé de la position de la masse 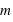 vers le centre de gravité de la Terre, et
vers le centre de gravité de la Terre, et 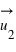 dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
dirigé orthogonalement de l'axe de rotation vers la masse. Donc le poids (=la force de pesanteur) ressenti sur la Terre dépend de notre position sur la Terre, il est lié à la fois au fait que la Terre n'est pas une sphère parfaite, et à la vitesse de rotation à une altitude donnée. Localement, il dépend aussi du fait que la masse de la Terre n'est pas répartie de manière homogène. La gravimétrie mesure de manière précise le champ de pesanteur à la surface terrestre.
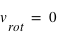 (aux pôles).
(aux pôles).
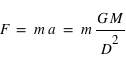 . En orbite,
. En orbite, 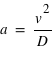 . Donc
. Donc 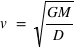 . Elle ne dépend pas de la masse du corps en orbite.
. Elle ne dépend pas de la masse du corps en orbite.
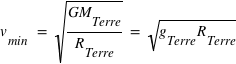 = 7,9 km.s-1.
= 7,9 km.s-1.
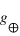 .
.
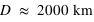 plutôt qu'à la surface de la Terre
plutôt qu'à la surface de la Terre 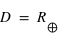 , et donc une force d'accélération,
, et donc une force d'accélération, 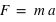 , bien moindre à fournir.
, bien moindre à fournir.
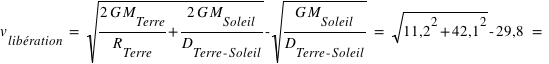 13,8 km.s-1.
13,8 km.s-1.
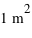 vaut
vaut 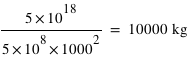 , soit environ 10 tonnes par mètre carré.
, soit environ 10 tonnes par mètre carré.