
Le champ stellaire analysé, autour de l'étoile HD 49933 (abondamment observée par une mission spatiale du CNES).
Crédit :
CDS
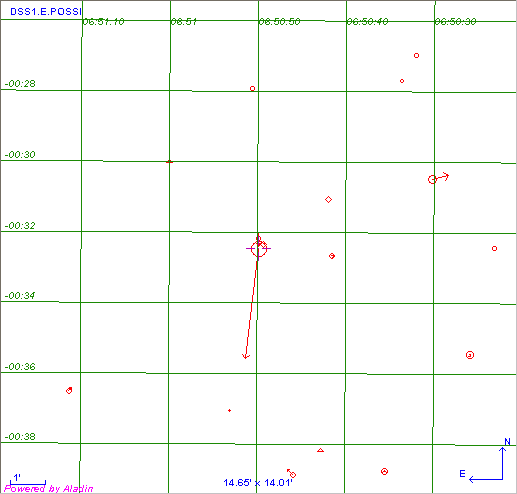
La carte des étoiles précédemment répertoriées, avec de plus leur mouvement propre.
Crédit :
CDS
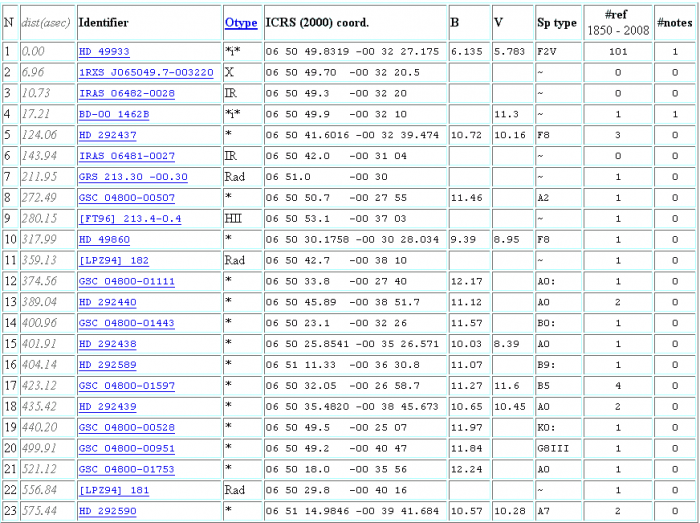
Le catalogue des étoiles précédemment répertoriées.
Crédit :
CDS
Un exemple : environnement d'une étoile
Les données astrométriques permettent une foultitude de choses, comme par exemple de précisément caractériser un champ autour d'un objet. Les figures ci-jointes décrivent de diverses manières l' environnement d'une étoile,
une carte, ou par
les coordonnées.
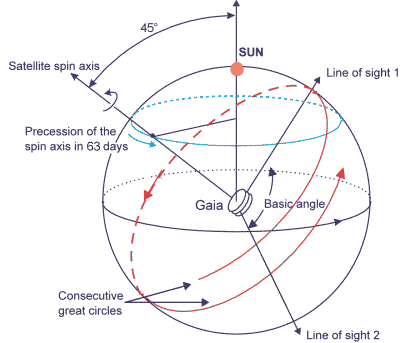
Le satellite Gaia, au point de
Lagrange L2, est animé d'un mouvement de rotation régulier, avec un axe (spin axis) orienté à 45 deg par rapport à la direction du Soleil. Il observe simultanément 2 régions du ciel (line of sight 1 et 2). Le mouvement de rotation induit le balayage de 2 grands cercles. La précession du mouvement de rotation induit l'évolution de ces grands cercles, pour observer tout le ciel.
Crédit :
ESA

Le montage de Gaia repose sur une structure octogonale très stable, pour la définition de l'angle entre les 2 lignes de visée astrométriques. Une 3ème ligne de visée est utilisée pour des mesures spectrométriques. La collecte du signal sur chaque ligne de visée implique 3 miroirs : les miroirs primaire et tertiaire se situent dans un même plan, et font face au miroir secondaire et au détecteur. Vu le nombre gigantesque de cibles à mesurer, le plan focal est composé d'une mosaïque de plusieurs dizaines de CCD. Le mode de lecture des CCD est original : les lignes du CCD sont positionnées exactement parallèlement au déplacement apparent de l'image suite à la rotation propre du satellite, et la pose et le transfert des charges d'un pixel à l'autre suivent le déplacement de l'image stellaire le long de la ligne du CCD.
Crédit :
EADS/Astrium
Le projet Gaia
Le principe de mesure de Gaia repose sur le balayage du ciel simultanément le long de deux lignes de visée. Le scénario de pointage met en oeuvre la rotation propre et la précession du satellite. Le montage optique s'appuie sur une structure stable.
 Définition
Définition
L'astrométrie a pour but de mesurer la position des astres, leur parallaxe et donc leur distance, leur mouvement propre. Elle opère un travail indispensable de repérage et d'arpentage.
Comment ?
L'agence spatiale européenne a exploité le satellite Hipparcos durant les années 1990, et lancé la mission Gaia fin 2013. Ces 2 missions ont pour but principal l'arpentage de l'Univers, obtenu par une très grande précision astrométrique.
Hipparcos comme Gaia sont des missions spatiales. L'écran de l'atmosphère terrestre est évité, la déviation d'un rayon lumineux au travers des couches atmosphériques étant bien trop importante par rapport à la précision recherchée, de l'ordre de la milliseconde d'arc.
La précision des missions Hipparcos et Gaia s'appuie sur le principe de l'observation simultanée de 2 champs stellaires, dans 2 directions faisant entre elles un angle fixé et stable (106.5 deg).
Comme un compas sert à repérer des distances (linéaires ou angulaires), de proche en proche les positions relatives des objets sont fixées les unes par rapport aux autres.
Gaia doit mesurer la précision d'un milliard d'objets dans la galaxies (soit 1% de son contenu stellaire), avec une précision de quelques millionièmes secondes d'arc pour les cibles les plus brillantes.
Performances attendues avec Gaia, pour une étoile de type G2
| magnitude | 10 | 15 | 20 |
| parallaxe (mas) | 0.007 | 0.027 | 0.3 |
Positions et mouvements
La
simulation ci-dessous permet de lire les positions et mouvements repérés par le satellite européen Hipparcos dans l'amas ouvert des Hyades. Noter que la précision des positions effectivement repérées par Hipparcos est infiniment meilleure que celle restituée par l'appliquette.

 Précision astrométrique et inégalité de Heisenberg
Précision astrométrique et inégalité de Heisenberg
Difficulté : ☆☆☆
Temps : 45 min
Cet exercice se propose de montrer que la précision astrométrique
d'un satellite tel Hipparcos ou Gaia peut être estimée par
l'application des inégalités de Heisenberg. On s'intéresse pour
ceci à la propagation d'un photon, issu d'un objet ponctuel à
l'infini, dont la trajectoire intercepte le miroir primaire de
détection (!). On munit l'espace d'un repère orthonormé 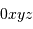 telle que le plan
telle que le plan 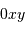 corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à
corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à 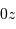 . On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
. On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
Question 1)
On s'intéresse à l'interception du photon selon la direction 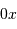 .
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe
.
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe 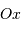 est inconnue, et que donc elle est
affublée d'une incertitude de position
est inconnue, et que donc elle est
affublée d'une incertitude de position 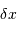 .
.
[2 points]
Réfléchir (!) à la formation d'image. Considérer une lentille
équivalente pour se simplifier la vie.
Question 2)
On rappelle qu'un échantillonnage par valeur entière correspond à
un bruit de numérisation de 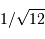 . En déduire
l'incertitude de mesure de la composant selon
. En déduire
l'incertitude de mesure de la composant selon 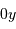 de la quantité
de mouvement du photon.
de la quantité
de mouvement du photon.
[1 points]
L'échantillonnage en position se fait ici par pas de largeur 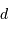 .
.
Question 3)
Par inégalité de Heisenberg, les incertitudes de position et
quantité de mouvement doivent vérifier :
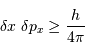
avec la quantité de mouvement totale 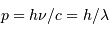 .
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
.
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
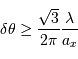
[3 points]
Déterminer d'abord 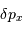 .
.
Déterminer 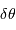 en fonction de
en fonction de 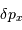 .
.
Question 4)
Faire l'application numérique pour Gaia, observant à la longueur
d'onde moyenne de 600 nm, avec 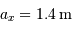 . Cela est-il
compatible avec les performances annoncées, de l'ordre de
. Cela est-il
compatible avec les performances annoncées, de l'ordre de 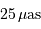 à la magnitude
à la magnitude 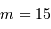 ? Pourquoi ?
? Pourquoi ?
[1 points]
Question 5)
La question précédente dimensionne l'incertitude pour 1 photon. On
montre plus loin dans le cours que pour 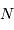 photons effectivement
détectés, l'incertitude est divisée par
photons effectivement
détectés, l'incertitude est divisée par 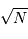 . Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
. Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
[1 points]





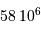
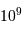
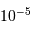

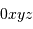 telle que le plan
telle que le plan 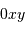 corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à
corresponde au miroir primaire de la
détection. La quantité de mouvement du photon incident est
quasiment parallèle à 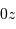 . On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
. On suppose que la formation d'image
suit parfaitement les lois de l'optique géométrique.
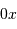 .
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe
.
Peut-on connaître la position de l'impact et de la réflexion du
photon sur le miroir? En déduire que le front d'onde incident est
découpé en tranche de largeur la dimension du miroir, que la
position selon l'axe 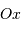 est inconnue, et que donc elle est
affublée d'une incertitude de position
est inconnue, et que donc elle est
affublée d'une incertitude de position 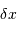 .
.
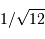 . En déduire
l'incertitude de mesure de la composant selon
. En déduire
l'incertitude de mesure de la composant selon 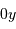 de la quantité
de mouvement du photon.
de la quantité
de mouvement du photon.
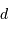 .
.
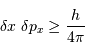
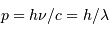 .
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
.
En déduire que l'incertitude de repérage de l'angle d'incidence du
photon vaut :
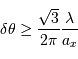
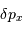 .
.
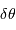 en fonction de
en fonction de 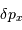 .
.
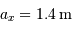 . Cela est-il
compatible avec les performances annoncées, de l'ordre de
. Cela est-il
compatible avec les performances annoncées, de l'ordre de 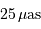 à la magnitude
à la magnitude 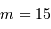 ? Pourquoi ?
? Pourquoi ?
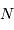 photons effectivement
détectés, l'incertitude est divisée par
photons effectivement
détectés, l'incertitude est divisée par 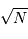 . Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.
. Combien de
photons doivent être détectés pour aboutir à la performance
annoncée.