Spectre du Soleil à haute résolution
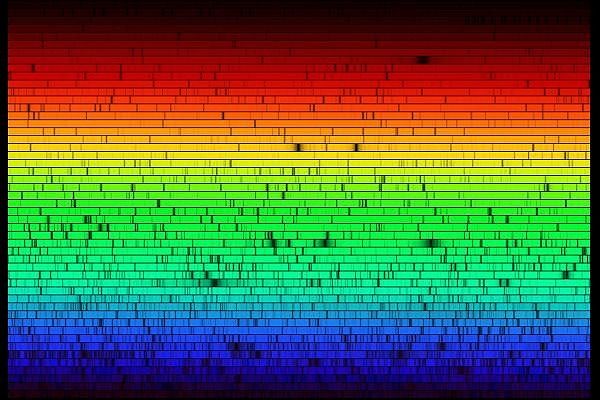
Le spectre solaire à haute résolution spectrale, observée avec un spectromètre à dispersion croisée. Les différents ordres d'interférence du spectromètre à haute dispersion ont été désenchevêtrés par la dispersion croisée.
Crédit :
NOAO
Dispersion croisée
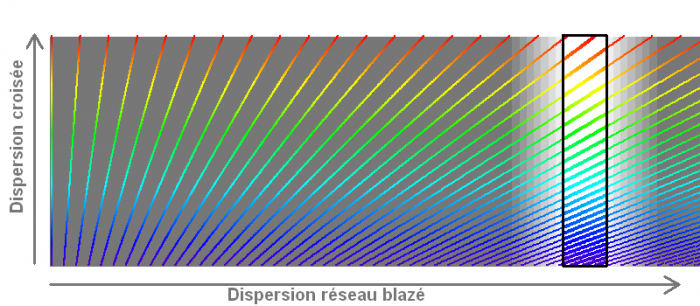
Schéma de principe :
une double dispersion permet l'enregistrement du spectre entier sur une caméra CCD. Un
réseau blazé disperse la lumière à haute résolution ; une dispersion à plus basse résolution, réalisée à l'aide d'un prisme, permet de distinguer les ordres entre eux. Le détecteur enregistre le signal dans les ordres élevés : chacun porte l'information spectrale, à haute résolution, dans un domaine de couleur différent. L'ensemble des ordres ainsi collectés permet de reconstituer le
spectre entier. Le réseau est blazé de façon à optimiser le rendement énergétique instrumental.
Crédit :
ASM
Réseau blazé
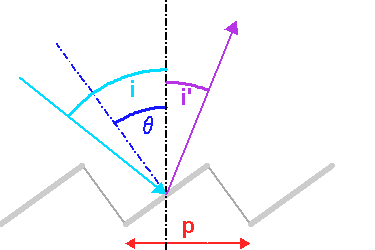
Profil d'un réseau blazé. Le profil en crête permet de réfléchir l'énergie dans un ordre d'interférence non nul.
Crédit :
ASM
Du bon usage des progrès technologiques
Les spectromètres pour la haute résolution spectrale ne datent pas d'hier. Mais l'avènement des caméras CCD, qui permettent d'enregistrer un signal sur 2 dimensions, a renouvelé le principe instrumental de la spectrométrie à haute résolution,
en ajoutant à la dispersion principale
une dispersion croisée, qui permet l'enregistrement simultané de tout le domaine spectral sur une caméra CCD.
Un spectromètre à réseau disperse la lumière dans ses ordres élevés, et les différents ordres sont séparés par une dispersion croisée obtenue à plus basse résolution. L'avantage d'une telle instrumentation est d'aboutir à un enregistrement simultané de tout le spectre, comme p.ex. ce spectre solaire.
Le spectromètre HARPS

Le spectromètre HARPS (High Accuracy Radial velocity Planet Searcher) est dédié à la recherche d'exoplanètes, par la méthode de mesure des vitesses radiales.
Crédit :
ESO/HARPS
Spectre obtenu par HARPS

Image d'un
spectre-échelle à haute résolution spectrale obtenu avec une caméra CCD. Le spectre de l'étoile apparaît ici sous l'aspect de bandes sombres.
L'étalonnage en longueur d'onde est apporté par les raies en émission d'une lampe spectrale (Thorium Argon), dont le spectre est intercalé avec celui de l'étoile, et enregistré simultanément.
Crédit :
ESO/HARPS
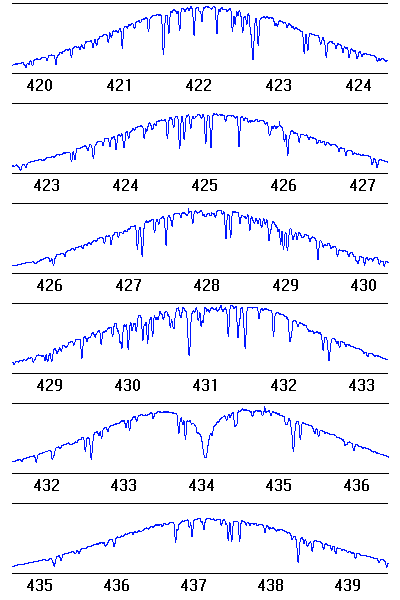
Spectre blazé obtenu avec le spectromètre Harps : la diffraction par chaque trait du réseau est responsable du profil d'étalement du flux.
Crédit :
ESO/HARPS
Le spectromètre HARPS
Le spectromètre HARPS dédié à la recherche d'exoplanètes est à l'heure actuelle le meilleur instrument de sa catégorie. Il atteint la résolution 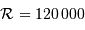 , en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.
, en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.
 Définition
Définition
Spectrométrie : étude des spectres.
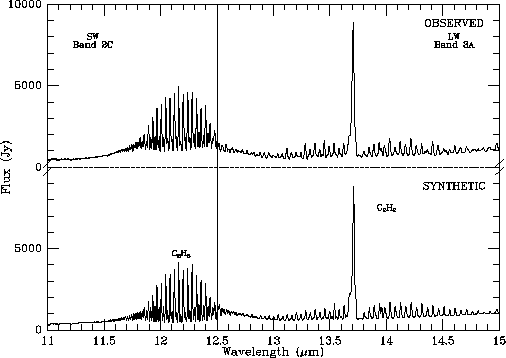
Spectre IR thermique de Saturne observé par le satellite ISO de l'Agence Spatiale Européenne, et interprétation des raies dues aux hydrocarbures présents dans la troposphère.
Crédit :
ESA
Pourquoi la spectrométrie à haute résolution ?
Bien distinguer l'identité spectrale des photons permet de remonter à la nature des éléments construisant le rayonnement, par absorption ou par émission.
La spectrométrie à haute résolution permet aussi, via l'analyse Doppler, des mesures très précises de vitesses radiales, comme p.ex. celles qui ont conduit à la découverte des planètes extrasolaires.
Le principe
Le principe du spectromètre HARPS (ESO/Observatoire de Genève) est expliqué ci-joint.
Principe du spectromètre HARPS 
 Le spectromètre HARPS
Le spectromètre HARPS
Difficulté : ☆☆☆
Temps : 45 min
Le spectromètre HARPS, mis en service au printemps 2003 à La Silla, l'un des sites chiliens de l'ESO, a pour but la recherche des exoplanètes. On se propose ici de retrouver quelques-unes des qualités qui lui permettent d'atteindre les objectifs scientifiques fixés.
Question 1)
Le spectromètre est installé derrière le télescope de 3.6 m de l'ESO. Sa pièce principale, le réseau, présente une hauteur 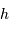 de 20 cm. Déterminer le grossissement
de 20 cm. Déterminer le grossissement 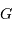 du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
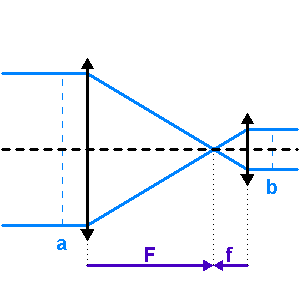
Rappel du montage afocal
Faisceau de sortie du montage afocal
Crédit :
ASM
Question 2)
Montrer qu'une déviation 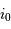 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 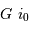 de l'angle dispersé.
de l'angle dispersé.
Relier la déviation de 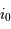 à celle de
à celle de 
Question 3)
Rappeler l'expression donnant les variations 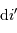 de l'angle de dispersion
de l'angle de dispersion 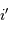 en fonction des variations de longueur d'onde
en fonction des variations de longueur d'onde 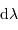 , du pas
, du pas 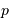 du réseau, et selon l'ordre d'interférence
du réseau, et selon l'ordre d'interférence 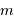 .
.
Le réseau envoie la lumière préférentiellement dans la direction 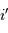 obéissant à :
obéissant à :
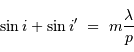
Différencier l'expression précédente.
Question 4)
On cherche à déterminer le champ objet maximal, qui permette
d'atteindre un pouvoir de résolution 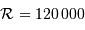 . Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
. Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
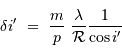
et conclure. On fera l'application numérique avec les données :
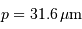 ,
, 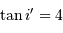 et un ordre d'interférence
et un ordre d'interférence 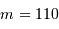 à
à 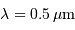 :
:
Question 5)
Justifier a posteriori l'hypothèse de non-divergence du faisceau. On pourra considérer un faisceau optique de longueur 8 m dans l'instrument.
Estimer la divergence en fonction de la longueur 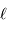 proposée et de l'angle
proposée et de l'angle 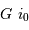 .
.
- Question 1
Aide :
Rappel du montage afocal
Faisceau de sortie du montage afocal

Crédit :
ASM
Solution :
Le grossissement du télescope doit transformer un faisceau parallèle de diamètre 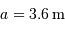 en un autre faisceau parallèle de diamètre
en un autre faisceau parallèle de diamètre 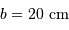 . Le grossissement doit donc vérifier :
. Le grossissement doit donc vérifier :
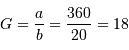
- Question 2
Aide :
Relier la déviation de 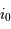 à celle de
à celle de 
Solution :
Vu le grossissement,
une déviation 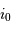 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 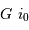 dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour
dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour 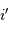 cette déviation
cette déviation 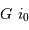 .
.
- Question 3
Aide :
Le réseau envoie la lumière préférentiellement dans la direction 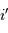 obéissant à :
obéissant à :
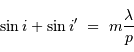
Aide :
Différencier l'expression précédente.
Solution :
Le réseau envoie la lumière préférentiellement dans la direction 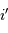 obéissant à :
obéissant à :
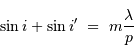
A incidence  fixée, la différentiation de la relation précédente donne :
fixée, la différentiation de la relation précédente donne :
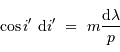
D'où la relation de dispersion :
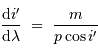
- Question 4
Aide :
Faire le lien entre 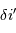 ,
, 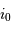 et le grossissement
et le grossissement 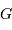 .
.
Solution :
La dispersion du réseau énonce :
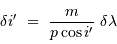
La résolution souhaitée entraîne la nécessité de distinguer des éléments spectraux de largeur :
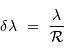
Par ailleurs, des variations de l'angle d'injection 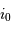 se traduisent par des variations de
se traduisent par des variations de 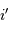 à hauteur de
à hauteur de 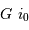 . On en déduit que les variations de l'angle
. On en déduit que les variations de l'angle 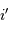 doivent être contraintes par :
doivent être contraintes par :
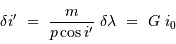
Et donc 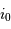 doit satisfaire :
doit satisfaire :
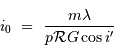
L'application numérique donne (avec 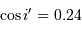 ) :
) :

On en déduit que le champ objet doit être extrêmement réduit. La fibre du spectromètre HARPS sélectionne ainsi uniquement 1" sur le ciel.
- Question 5
Aide :
Estimer la divergence en fonction de la longueur 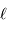 proposée et de l'angle
proposée et de l'angle 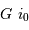 .
.
Solution :
Une déviation angulaire 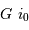 avec un bras de levier de longueur
avec un bras de levier de longueur 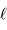 se traduit par une déviation linéaire
se traduit par une déviation linéaire 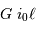 .
.
L'application numérique donne 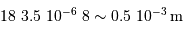 . Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
. Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.






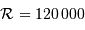 , en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.
, en proposant une excellente stabilité. Les mesures sont stables et reproductibles, sur une durée de plusieurs années, à mieux que le milliardième près. Les spectres de HARPS sont obtenus avec les différents ordres d'interférences repliés sur une image ; l'image, traitée, conduit au spectre.


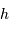 de 20 cm. Déterminer le grossissement
de 20 cm. Déterminer le grossissement 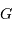 du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.
du montage afocal permettant un éclairement optimum du réseau, en supposant un faisceau non divergent.

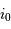 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 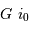 de l'angle dispersé.
de l'angle dispersé.
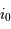 à celle de
à celle de 
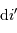 de l'angle de dispersion
de l'angle de dispersion 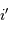 en fonction des variations de longueur d'onde
en fonction des variations de longueur d'onde 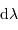 , du pas
, du pas 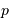 du réseau, et selon l'ordre d'interférence
du réseau, et selon l'ordre d'interférence 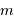 .
.
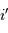 obéissant à :
obéissant à :
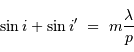
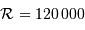 . Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
. Montrer que cette performance nécessite un faisceau émergeant du spectromètre de taille angulaire limitée à
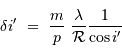
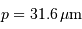 ,
, 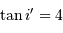 et un ordre d'interférence
et un ordre d'interférence 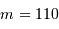 à
à 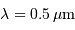 :
:
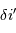 ,
, 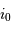 et le grossissement
et le grossissement 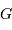 .
.
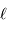 proposée et de l'angle
proposée et de l'angle 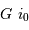 .
.
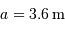 en un autre faisceau parallèle de diamètre
en un autre faisceau parallèle de diamètre 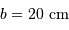 . Le grossissement doit donc vérifier :
. Le grossissement doit donc vérifier :
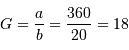
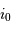 dans le champ objet se traduit par une variation
dans le champ objet se traduit par une variation 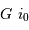 dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour
dans le champ image. Le spectromètre, attaqué par une onde incidente déviée, renvoie la lumière dans une direction déviée d'autant. On retrouve donc pour 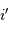 cette déviation
cette déviation 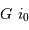 .
.
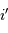 obéissant à :
obéissant à :
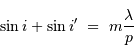
 fixée, la différentiation de la relation précédente donne :
fixée, la différentiation de la relation précédente donne :
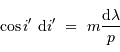
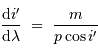
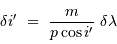
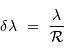
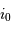 se traduisent par des variations de
se traduisent par des variations de 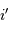 à hauteur de
à hauteur de 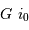 . On en déduit que les variations de l'angle
. On en déduit que les variations de l'angle 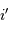 doivent être contraintes par :
doivent être contraintes par :
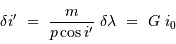
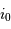 doit satisfaire :
doit satisfaire :
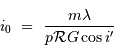
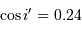 ) :
) :

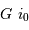 avec un bras de levier de longueur
avec un bras de levier de longueur 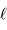 se traduit par une déviation linéaire
se traduit par une déviation linéaire 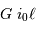 .
.
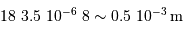 . Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.
. Ces 0.5 mm sont totalement négligeables devant la hauteur du faisceau de 20 cm.