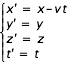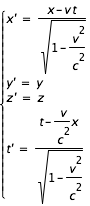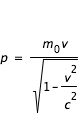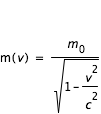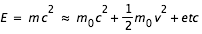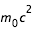La gravitation universelle et la relativité
Auteur: Jean-Eudes Arlot
- Introduction
- La gravitation newtonnienne
- Les limites de la gravitation universelle
- En savoir plus: l'excès d'avance du périhélie de Mercure
- La constante de la gravitation
- Exercice
- Les principes de la relativité
- La relativité galiléenne
- Les limites de la relativité galiléenne
- La relativité d'Einstein
- La relativité restreinte
- En savoir plus: la dynamique relativiste
- La relativité générale
- Les preuves expérimentales de la relativité générale
- QCM
Introduction
 Introduction
Introduction
La gravitation universelle a expliqué beaucoup de choses mais reste en elle-même inexpliquée. Une nouvelle approche de la description de l'univers va permettre d'expliquer certaines choses que la gravitation universelle de Newton n'expliquait pas.
La gravitation newtonnienne
Les limites de la gravitation universelle
Rappelons la loi de Newton : F = -Gmm'/r2 où F est la force exercée l'un sur l'autre par deux corps de masses respectives m et m' séparés d'une distance r. G est appelée constante de la gravitation.
D'autre part, le principe d'inertie découvert par Galilée stipule qu'un corps qui se déplace sans interaction avec l'extérieur, continuera sur une trajectoire rectiligne indéfiniment. Newton ajoutera que le seul moyen de modifier cette trajectoire est d'utiliser une force : un objet subissant une force accélère d'une quantité inversement proportionnelle à la masse de l'objet dans la direction de la force.
Tous ces principes vont nous permettre de décrire les mouvements dans le système solaire mais, avouons-le, ils n'expliquent pas grand-chose. On est en présence d'une action à distance. Pourquoi les corps s'attirent-ils ? Nul ne le sait. Avant Newton, on pensait que des anges poussaient les planètes sur leurs orbites ; après Newton, on sait que les anges ne poussent pas les planètes mais les tirent vers le corps central pour contrecarrer le principe d'inertie ! Aucun mécanisme n'a été mis en évidence pour expliquer l'action de cette force.
La théorie de Newton explique aussi l'aplatissement du globe terrestre et permet de décrire correctement les marées. On avait bien pensé auparavant que la Lune pouvait attirer l'eau des mers mais alors la marée aurait dû n'être haute que du côté de la Lune. Newton l'explique : la Terre tourne autour du Soleil, elle n'est pas dans un repère galiléen et subit l'attraction de la Lune. Rien ne maintient la Terre pendant que l'eau monte vers la Lune. Le différentiel des forces explique bien les marées hautes de part et d'autre de la Terre. Enfin la gravitation universelle ne s'applique pas qu'au système solaire mais à l'univers tout entier.
Elle n'explique pas l'excès d'avance du périhélie de Mercure.
Pour expliquer ce dernier point, il est nécessaire de faire appel à la théorie de la relativité générale pour laquelle :
- il n'y a pas de temps absolu
- la notion de référentiel galiléen n'est plus pertinente
- il n'y a plus de forces à distance mais un champ de gravité se propageant à la vitesse de la lumière.
En savoir plus: l'excès d'avance du périhélie de Mercure
 En savoir plus
En savoir plus
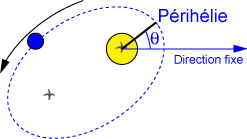
Périhélie : point où Mercure est au plus près du Soleil. l'angle θ est l'angle entre une direction fixe et la direction du périhélie.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Le système Soleil Mercure n'est pas isolé dans l'espace et subit des perturbations gravitationnelles qui peuvent faire varier l'angle θ qui donne la position du périhélie de Mercure. Ainsi θ va varier et le périhélie va sembler "avancer" au cours du temps. la mécanique newtonnienne permet de calculer cette avance mais les observations ont montré que le périhélie avance plus rapidement que prévu. Le Verrier a cherché une planète inconnue dont les perturbations expliqueraient cet excès d'avance mais ne l'a pas trouvé. Il faudra attendre Einstein et la théorie de la relativité générale pour l'expliquer.
La constante de la gravitation
Dans la formule de Newton ci-dessus, on remarque l'existence d'une constante G. A quoi correspond-elle ? Quelle est sa valeur ? En fait, la mesure des distances et des périodes dans le système solaire ne nous fournit que le produit Gm de la constante G avec la masse du corps central. On connaît donc G x (masse solaire) en mesurant les positions des planètes, G x (masse terrestre) en mesurant le mouvement de la Lune, G x (masse de Jupiter) en mesurant les positions des satellites de Jupiter, etc. La mesure absolue de G a été faite par Cavendish (1731-1810) en 1798. Pour cela il réalise une expérience désormais célèbre : il mesure l'attraction de deux boules de plomb de 150 kg chacune sur de petites billes par l'intermédiaire d'un pendule de torsion. Il pourra dire : j'ai pesé la Terre ! La valeur de cette constante est 6,672 59 x 10-11 m3 kg-1 s-2.
Une question se pose aussi : la constante de la gravitation est-elle vraiment constante ou se modifie-t-elle au cours du temps ? Il a été impossible de mesurer une variation de cette constante mais cette variation, si elle existe, ne peut être que faible. En effet, en supposant que cette constante ait varié de 10% au cours du dernier milliard d'années, les conditions de rayonnement du Soleil auraient été telles que la vie aurait été impossible sur Terre à cette époque. La variation de cette constante ne peut donc être que beaucoup plus faible que cela.
Exercice
 La constante de gravitation
La constante de gravitation
Question 1)
Cette détermination nous permet de connaître la masse des corps du système solaire et de résoudre des problèmes tels que :
quelle serait la durée de révolution d'une bille de masse négligeable autour d'une masse d'un kilogramme situé à un mètre dans l'espace ?
Les principes de la relativité
Après avoir vu la gravitation universelle au sens de Newton, venons-en au principe de relativité. Ce principe n'est pas récent. Dès les prémices de la mécanique, la question qui s'est posée est : les lois de la physique que l'on met à jour restent-elles invariantes dans n'importe quel référentiel ? Y-a-t-il un référentiel absolu ? C'est à cette question fondamentale que les théories de la relativité vont tenter de répondre.
En 1905, A. Einstein (1879-1955) publie sa théorie de la relativité restreinte et, en 1916, celle de la relativité générale.
La relativité galiléenne
Avant même la découverte de la gravitation universelle par Newton, Galilée énonce le principe de l'inertie : tout corps abandonné à lui-même et ne subissant aucune force extérieure, est animé d'un mouvement rectiligne uniforme. On appellera "référentiels galiléens" des systèmes de référence en mouvement de translation rectiligne uniforme les uns par rapport aux autres. Pour passer d'un référentiel R à un référentiel R' animé d'une vitesse v parallèle à l'axe des abscisses, le changement de variable est de la forme :
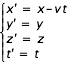
Dans cette transformation dite "galiléenne", les lois de la mécanique et de la physique sont supposées être invariantes. Les vitesses s'additionnent. Afin de respecter le principe d'inertie, Newton sera amené à introduire un temps absolu et un espace absolu universel.
Les limites de la relativité galiléenne
Ce système simple va vivre pendant plus d'un siècle et la mécanique céleste va décrire merveilleusement la dynamique du système solaire jusqu'à ce que deux grains de sable se glissent dans la machine. L'un sera l'inexplicable excès de l'avance du périhélie de Mercure. La mécanique classique sera impuissante devant ce problème. L'autre viendra de la découverte de l'électromagnétisme. En 1873, J. Maxwell (1831-1879), physicien écossais, publie les équations générales des champs électromagnétiques, dites "équations de Maxwell". On constate alors que ces équations ne sont pas invariantes. Effectivement, la composition des vitesses ne fonctionnent pas avec la vitesse de la lumière qui ne dépend pas de la vitesse de la source (cela se remarquerait lors de l'observation des étoiles doubles) et ne peut être composée avec une autre vitesse. Serait-ce dû à l'existence d'un "éther" dans lequel la lumière se déplace par vibration ? On chercha alors à déceler un mouvement par rapport à l'éther. En particulier, on devait pouvoir mesurer la vitesse d'un mobile en mesurant les modifications des lois physiques entraînées par le déplacement. Ce fut alors la célèbre expérience de Michelson qui consiste à mesurer la vitesse de la lumière dans deux directions perpendiculaires. Cette expérience fut faite en divers lieux, à 6 mois d'intervalle (la vitesse de la Terre change de sens) pendant des dizaines d'années et jamais on ne trouva un changement dans la vitesse de la lumière. Le mouvement de la Terre était indétectable avec cette méthode. Les équations de Maxwell étaient-elles fausses ? En fait non, c'était la transformation galiléenne qui n'était pas correcte. H. Poincaré montra que les équations de Maxwell étaient invariantes si on leur appliquait une transformation particulière, dite "transformation de Lorentz".
La relativité d'Einstein
La relativité restreinte
Einstein va réussir à étendre le principe de relativité de la mécanique à la physique à partir de deux postulats :
- tous les référentiels galiléens sont équivalents pour la formulation des lois physiques ;
- la vitesse de la lumière dans le vide est constante par rapport à n'importe quel système galiléen et est indépendante du mouvement de la source.
Ces deux postulats étaient bien sûr incompatibles avec la transformation galiléenne qui postule qu'il existe un temps absolu et que la mesure d'une longueur est indépendante du mouvement du système de référence. Einstein va montrer les erreurs de ces postulats. En particulier, il montre la relativité de la notion de simultanéité qui n'a de signification que dans un système galiléen déterminé, ce qui entraîne la relativité de la notion de longueur. Longueur et temps sont liés. La transformation galiléenne doit, comme prévu, être remplacée par la transformation de Lorentz :
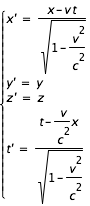
pour deux repères ayant leurs axes parallèles et en déplacement relatif selon l'axe x.
La loi de composition des vitesses n'est plus celle du système galiléen.
Cette transformation va entraîner la contraction des longueurs et la dilatation des durées pour les corps en mouvement. On remarquera que pour des vitesses relatives petites devant c (i.e. v/c petit), la transformation de Lorentz se réduit à la transformation de Galilée.
En savoir plus: la dynamique relativiste
 En savoir plus
En savoir plus
Les lois de la dynamique newtonnienne sont aussi à modifier : elles doivent être invariantes dans une transformation de Lorentz.
La quantité de mouvement p = mv devient :
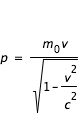
Dans la mécanique newtonnienne, la notion de masse a deux sens : sa détection par son poids (masse gravifique) et sa détection par sa résistance au mouvement (masse inerte). Ces masses sont proportionnelles et on choisit les unités de façon à ce qu'elles soient identiques. En identifiant l'expression ci-dessus avec p=m(v).v, on en déduit que :
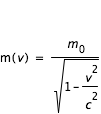
où m0 est la masse au repos.
La relativité d'Einstein introduit donc la notion de masse au repos et induit une augmentation de la masse avec la vitesse.
Quant à la loi de conservation de l'énergie, elle devient :
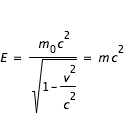
soit en développant :
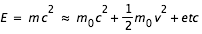
La théorie d'Einstein introduit un terme nouveau : 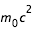
qui correspond à l' "énergie interne" en plus de l'énergie cinétique et il y a ainsi équivalence entre masse et énergie.
Tous ces faits nouveaux ont été vérifiés par la physique des particules qui permet d'obtenir de très grandes vitesses. Aux basses vitesses, on retrouve les lois de la dynamique newtonnienne.
La relativité générale
La relativité restreinte n'a cependant pas résolu tous les problèmes. Elle s'est montrée incapable d'incorporer la gravitation de manière satisfaisante et certaines expériences semblent toujours prouver qu'il existe un référentiel absolu. Par exemple, l'expérience du pendule de Foucault semble indiquer que l'on peut mesurer le mouvement de la Terre par rapport à un référentiel absolu. Où donc se trouve la contradiction ? Einstein va étendre pour cela la relativité restreinte à la gravitation. Pour cela Einstein va énoncer le principe d'équivalence. L'identité entre la masse gravifique et la masse inertielle devient un postulat de base de la théorie. Ainsi, il n'est pas possible, localement, de distinguer une force créée par une accélération d'une force créée par la gravitation. Cette identité a conduit Einstein à penser qu'un laboratoire en chute libre dans un champ gravitationnel constitue en quelque sorte l'extension naturelle du concept de système de référence inertiel de l'ancienne mécanique. On est ainsi amené à postuler que "tous les systèmes de référence en chute libre sont équivalents pour l'expression des lois physiques non gravitationnelles, quel que soit leur état de mouvement et leur localisation". Cet énoncé constitue ce qu'on appelle aujourd'hui le principe d'équivalence d'Einstein.
Il faut souligner à ce propos que ce principe n'édicte rien sur la description des phénomènes gravitationnels eux-mêmes. Ainsi, il ne postule pas que deux laboratoires en chute libre situés en des endroits différents vont trouver la même valeur pour la constante de la gravitation G (étant admis qu'ils sont munis d'horloges et de mètres de même fabrication). Autrement dit, le principe d'équivalence d'Einstein ne rejette pas a priori que la "vraie théorie relativiste de la gravitation" puisse prédire que G varie avec le temps et le lieu. Ce principe permet donc des généralisations de la relativité générale, généralisations dont les vérifications font l'objet de nombreuses recherches actuelles.
L'idée qu'en présence d'un champ gravitationnel, ce sont les référentiels en chute libre qui doivent remplacer les référentiels inertiels en amène très naturellement une autre : les référentiels en chute libre ne peuvent être que locaux, car un vrai champ de gravitation (celui de la Terre par exemple) n'est pas uniforme. En effet, la non uniformité entraîne qu'aucun mouvement global du système de référence ne peut supprimer partout le champ de la Terre. D'où l'idée que le principe d'équivalence d'Einstein, qui est purement local, n'interdit pas à la géométrie de l'espace-temps de changer d'un point à un autre. Au contraire, un tel changement de géométrie permet de résoudre le problème de la gravitation avec une extrême élégance conceptuelle. Le principe d'inertie galiléen nous dit qu'en l'absence de tout champ de force, un point matériel a un mouvement rectiligne uniforme dans tout référentiel galiléen. Or, une droite est une géodésique de l'espace euclidien. Il est dès lors naturel de considérer le mouvement d'une particule en chute libre dans un champ gravitationnel comme défini par une géodésique d'une métrique plus complexe qu'une métrique euclidienne. En fait, Einstein a introduit une généralisation dite "pseudo-riemanienne" de la métrique spatio-temporelle de la relativité restreinte.
Nous donnons ci-dessous une analogie qui permet de comprendre pourquoi une métrique non euclidienne peut rendre compte de façon simple d'une force de gravitation.
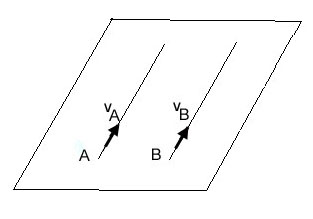
Plan euclidien P : deux corps A et B initialement doués de vitesse vA = vB et suivant des géodésiques de P (droites) vont rester à distance constante : il n'y a pas de gravitation dans cet univers : A et B ne "s'attirent" pas.
Crédit : CNRS/Jean-Eudes Arlot
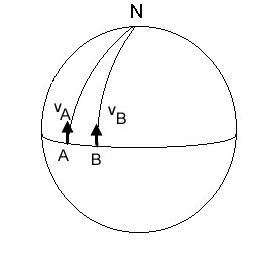
Sphère S : deux corps A et B initialement doués de vitesse vA = vB sur l'équateur et suivant des géodésiques de S (grands cercles) vont se rapprocher et se rejoindre au pôle N : il y a de la gravitation dans cet univers : A et B "s'attirent".
On peut donc décrire la gravitation comme une manifestation de la courbure d'une métrique.
Crédit : CNRS/Jean-Eudes Arlot
Les preuves expérimentales de la relativité générale
La théorie de la relativité générale a permis d'expliquer plusieurs phénomènes importants :
- l'excès d'avance du périhélie de Mercure se trouve parfaitement modélisé dans le cadre de la relativité générale ;
- la courbure des rayons lumineux passant près d'une masse est détectée en observant les étoiles proches du Soleil pendant une éclipse ;
- les mirages gravitationnels (effet de lentille d'une masse importante se trouvant sur le trajet de rayons lumineux) ont été observés (cf. ci-dessous) ;
- l'expansion de l'univers découverte par Hubble grâce au décalage spectral vers le rouge des galaxies.

Cette image du télescope spatial HST de l'amas de galaxies Abell 2218 montre un exemple spectaculaire de lentille gravitationnelle. Les arcs visibles sur l'image sont des mirages créés par le champ gravitationnel de l'amas. L'amas est tellement massif et compact que les rayons lumineux passant à travers cet amas sont déviés et, comme à travers une lentille, forment une nouvelle image. Ce processus déforme l'image primaire des objets se trouvant beaucoup plus loin que l'amas de galaxies provoquant le phénomène.
Crédit : NASA/STSCI
QCM
Réponses aux QCM
pages_relativite-einstein/mctc-qcm-relativite.html
QCM
- Question 1
Solution : réponse 3)
(
oui, la relativité générale explique que la masse du Soleil déforme l'espace et modifie le mouvement de Mercure par rapport à un mouvement newtonien simple
)
 Introduction
Introduction