Effet sur la matière
Pour comprendre comment l’on peut détecter une onde gravitationnelle, il faut se demander qu’est-ce qui se passe pour la matière quand l’amplitude caractéristique h des termes non nuls de la matrice 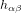 oscille autour de sa valeur normale,
oscille autour de sa valeur normale, 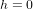 .
.
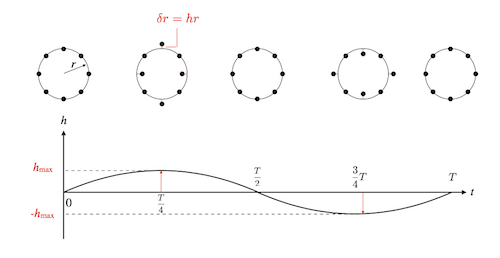
Considérons donc le cadran d’une montre imaginaire et huit particules disposées à 1h30, 3h, 4h30, 6h, 7h30, 9h, 10h30 et 12h (Figure ci-dessous). Soit r le rayon du cercle qui passe par les huit particules. Les positions des huit particules sont perturbées par le passage d’une onde gravitationnelle sinusoïdale avec une période T. Nous choisissons le temps 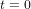 de telle manière que
de telle manière que 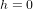 pour
pour 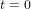 . A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
. A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
A 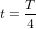 , h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
, h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
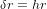 (1).
(1).
A 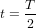 ,
, 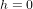 . Donc, les particules sont revenues à la position initiale. A
. Donc, les particules sont revenues à la position initiale. A 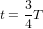 ,
, 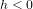 , donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à
, donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à 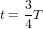 a la même forme que l’ellipse à
a la même forme que l’ellipse à 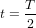 tournée de 90˚. A
tournée de 90˚. A 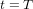 , les particules reviennent pour la deuxième fois à la position initiale.
, les particules reviennent pour la deuxième fois à la position initiale.
L’effet du passage de l’onde gravitationnelle est donc celui de générer une vibration de la structure de l’espace-temps qui met en oscillation toutes les longueurs.
L'interférométrie
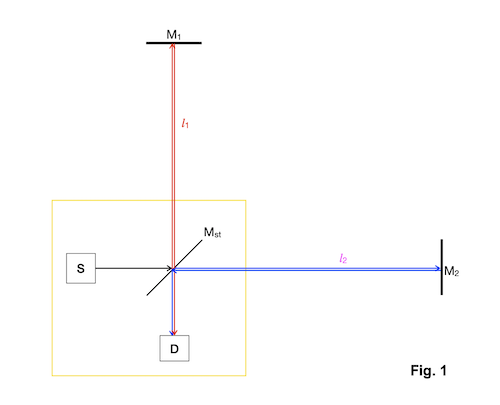
L’instrument que l’on utilise pour mesurer des variations de distance très très petites est un interféromètre. La raison de ce nom nous sera claire bientôt. Le principe de fonctionnement d’un interféromètre consiste à utiliser un système de miroirs pour faire arriver un faisceau laser d’une source à un détecteur en lui faisant emprunter deux chemins différents, 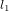 et
et 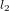 (Fig. 1).
(Fig. 1).
Un faisceau laser sort de la source S, située dans le bâtiment principal, dont les murs sont marqués en jaune. Le faisceau laser rencontre le miroir semi-transparent (la plaque séparatrice de verre semi-argentée) 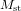 . Une partie de la lumière est réfléchie et redirigée vers le miroir
. Une partie de la lumière est réfléchie et redirigée vers le miroir 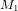 . Une autre partie continue son chemin en ligne droite vers le miroir
. Une autre partie continue son chemin en ligne droite vers le miroir 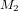 . La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers
. La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers 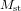 . Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers
. Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers 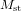 . Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
. Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
Les ondes monochromatiques qui arrivent au détecteur par les deux chemins ont été émises avec la même phase, s’agissant du même faisceau laser qui a été séparé en deux, mais elles y arriveront avec des phases différentes si les longueurs 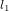 et
et 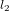 des deux chemins après leur séparation sont
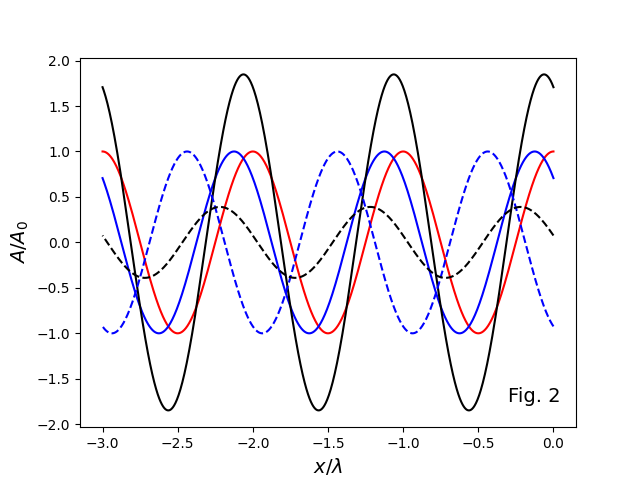
des deux chemins après leur séparation sont 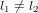 . Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins
. Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins 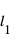 et
et 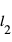 est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (
est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (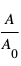 est le rapport entre l’amplitude
est le rapport entre l’amplitude 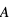 mesurée par le détecteur et l’amplitude
mesurée par le détecteur et l’amplitude 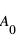 émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin
émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin 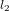 (5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
(5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
En général, 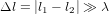 , où
, où  est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si
est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si 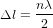 et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si
et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si 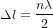 et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.
et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.
Interféromètres

Interféromètres LIGO (Hanford à gauche et Livingston au centre) et VIRGO (à droite)
Crédit :
MIT-CNRS
Les principaux interféromètres pour la détection d’ondes gravitationnelles sont construits à Hanford (Washington) et Livingstone (Louisiane) par la collaboration américaine LIGO, et à proximité de Pise par la collaboration franco-italienne VIRGO. Un quatrième interféromètre, beaucoup plus petit, a aussi été construit à Hanover par la collaboration anglo-allemande GEO600. D’autres interféromètres seront bientôt opérationnels.
Dans les trois cas, l’interféromètre est constitué d’une unité centrale et de deux bras, qui font 4 km de long dans le cas de LIGO, 3 km de long dans le cas de VIRGO et 600 m de long dans le cas de GEO600. L’unité centrale contient la source laser, le détecteur et la lame séparatrice, un miroir semi-transparent qui sépare la lumière en un faisceau réfléchi et un faisceau transmis. Les deux faisceaux sont envoyés dans les deux bras de l’interféromètre, des tubes sous vide qui se terminent avec des miroirs qui réfléchissent les deux faisceaux vers l’unité centrale. Des systèmes de miroirs sont utilisés afin que la lumière fasse plusieurs aller-retours dans chaque bras avant d’être envoyée au détecteur, de telle manière que tout se passe comme si les bras étaient des centaines de fois plus longs (la vitesse de la lumière est tellement élevée que la lumière peut faire des centaines d’aller-retours dans un temps court par rapport à la période des ondes gravitationnelles, déterminée par la période orbitale des systèmes binaires qui les produisent).
La difficulté la plus grande est due à la présence de nombreuses sources de bruit qui pourraient mettre en vibration les miroirs d’un interféromètre simulant les effet d’une onde gravitationnelle (activité sismique, vent, circulation routière, bruit thermique). La détection d’une onde gravitationnelle avec au moins deux interféromètres à deux endroits différents de la planète est nécessaire pour exclure ces formes de bruits, qui ne peuvent pas générer la même forme d’onde simultanément à plusieurs milliers de kilomètres de distance.
Détection des ondes gravitationnelles
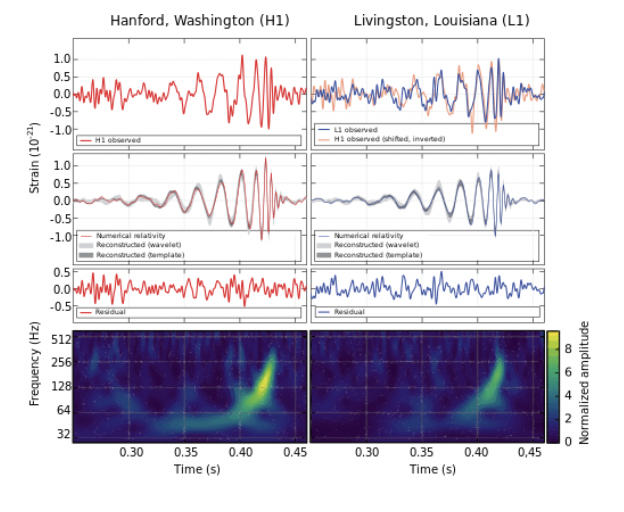
Détection par la collaboration LIGO des ondes gravitationnelles le 14 septembre 2015
Crédit :
LIGO
La première détection d’ondes gravitationnelles a été réalisée aux Etats Unis, par la collaboration LIGO, le 14 septembre 2015, même si la découverte n’a été annoncée que le 11 février 2016, après de nombreuses vérifications. Les miroirs de l'interféromètre de Livingston sont entrés en vibration, puis, 7 millisecondes plus tard, le même phénomène s’est produit dans les miroirs de l’interféromètre de Hanford. La fréquence des oscillations a augmenté et leur amplitude a cru pendant 0,2 seconde, puis elles se sont amorties. Les figures ci-dessus montrent la fréquence du signal mesurée à Livingston et Hanford en fonction du temps.
Ce signal a été appelé GW150914. GW est un acronyme pour Gravitational Waves. Les chiffres qui suivent donnent l’année, le mois et le jour de l’événement. L’amplitude de la perturbation était trop faible pour qu’un être humain puisse s’apercevoir de quoi que ce soit, mais on a remarqué que la fréquence du signal correspondait à des longueurs d’onde audibles. En l’amplifiant énormément, on entend ce qui pourrait ressembler au pépiement d’un oiseau.
Au maximum de l’intensité, la variation de distance entre l’unité centrale et les miroirs au fond des bras a été de un sur 1021 (graphiques sur la première ligne de la figure ci-dessus). La similarité des formes d’onde observées à Livingston et à Hanford (respectivement, la courbe bleue et la courbe rouge dans la figure en haut à droite), ainsi bien que la presque simultanéité des deux détections, cohérente avec une perturbation qui voyage à la vitesse de la lumière (la distance entre Hanford et Livingstone est d’environ 2000 km) supporte fortement l’interprétation que le signal mesuré soit dû au passage d’une onde gravitationnelle. Des ondes sismiques ne pourraient pas se propager à une vitesse supérieure à la vitesse du son dans les roches (de l’ordre de 10 km/s).
Un autre argument qui supporte cette interprétation est la similarité entre la forme d’onde observée et le signal prédit par les simulations numériques des ondes gravitationnelles générées par la coalescence de trous noirs. Les deux graphiques sur la deuxième ligne de la figure ci-dessus comparent ces prédictions (les courbes rouge et bleue dans les graphiques du milieu) à l’évolution de l’amplitude des oscillations, après que celles-ci ont été nettoyées du bruit (les courbes grises au-dessous des courbes rouges et bleues montrent le signal nettoyé). Cette comparaison a non seulement confirmé l’origine gravitationnelle du signal mesuré mais elle a aussi permis de reconstruire certains aspects de l’événement astrophysique qui l’a produit.
Les ondes gravitationnelles viendraient d’un système binaire de trous noirs de 35 et 30 masses solaires. Leur émission correspond aux dernières orbites des deux trous noirs et à leur coalescence finale, qui aboutit à la formation d’un seul trou noir de 62 masses solaires, la masse-énergie des 3 masses solaires manquantes ayant été convertie en ondes gravitationnelles. La puissance émise durant les dernières 20 millisecondes de la coalescence aurait été de 3 x 1056 erg/s, soit 50 fois la puissance lumineuse totale de toutes les étoiles dans l’Univers visible.
Le signal provenait de la direction de la constellation du Sagittaire. A partir de l’amplitude du signal (ou bien de la faiblesse du signal, pour phénomène d'une telle puissance), on a estimé que l’événement s’est passé à une distance de 440 mégaparsecs, donc bien au-delà de l’Univers local. Les ondes gravitationnelles que nous avons détectées le 14 septembre 2015 ont donc voyagé dans l’espace pendant 1,4 milliards d’années avant de nous parvenir.
Cette détection d'ondes gravitationnelles ouvre de nouvelles fenêtres sur l’Univers. Les premiers éléments enthousiasmants sont la détection expérimentale d’un phénomène physique prédit mais non observé, et qu'il s'agit d'une nouvelle confirmation de la théorie de la relativité d’Einstein. L’intérêt des détections suivantes (GW151226, GW170104) et des prochaines porteront plus sur les connaissances astrophysiques qu’elles apportent sur les propriétés des trous noirs et la fréquence de ce type d’événements. Le télescope restera toujours l’instrument principal de l’astronome, mais la détection d’ondes gravitationnelles aussi bien que celle des neutrinos nous offre la possibilité d’étudier les astres par d’autres manières que l’observation de leur lumière.
Les limites les plus importantes au développement de l’astronomie des ondes gravitationnelles restent la taille maximale des interféromètres que l’on peut construire et les bruits dérivant de nombreux phénomènes qui se passent sur notre planète. La prochaine étape sera donc le développement d’un interféromètre dans l’espace. L’Agence Spatiale Européenne a déjà un projet dans ce sens. Il s’agit de LISA (Laser Interferometer Space Antenna). Dans LISA, l’unité centrale et les miroirs au fond des bras seront remplacés par trois astronefs séparées par des distances de millions de kilomètres. La mission LISA devrait devenir opérationnelle après 2030. Une étude préliminaire des bruits auxquels on peut s’attendre dans les mesures avec LISA vient d’être plubiée en 2017.
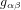 qui définissent la métrique.
qui définissent la métrique.
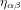 , pour laquelle
, pour laquelle 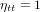 ,
, 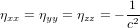 et
et 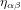 quand
quand 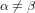 . La personne qui a failli recevoir un pot de fleurs sur la tête ne partagera bien sûr pas cet avis, mais c’est la raison pour laquelle l’amplitude des ondes gravitationnelles est donnée par la matrice :
. La personne qui a failli recevoir un pot de fleurs sur la tête ne partagera bien sûr pas cet avis, mais c’est la raison pour laquelle l’amplitude des ondes gravitationnelles est donnée par la matrice :
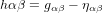 (1),
(1),
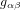 et la métrique de Minkowski
et la métrique de Minkowski 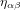 .
.
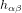 correspond donc à une perturbation de la métrique.
correspond donc à une perturbation de la métrique.
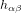 oscille autour de sa valeur normale,
oscille autour de sa valeur normale, 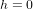 .
.
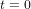 de telle manière que
de telle manière que 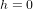 pour
pour 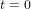 . A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
. A cet instant initial, il n’y a pas de perturbation, donc les particules forment un cercle parfait.
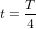 , h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
, h atteint la valeur maximale. Notez que nous avons écrit en italique l’amplitude h de l’onde gravitationnelle pour ne pas la confondre avec le h d’heure. Les particules à 6h et 12h se sont éloignées du centre du cercle, alors que les particules à 3h et 9h s’en sont approchées. Le cercle est devenu une ellipse, dont le grand axe est l’axe vertical. La distance de laquelle les particules à 3h et 9h se sont rapprochées du centre est égale à la distance de laquelle les particules à 6h et 12h se sont éloignées du centre. Toutes les quatre se sont déplacées d’une longueur :
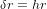 (1).
(1).
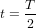 ,
, 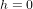 . Donc, les particules sont revenues à la position initiale. A
. Donc, les particules sont revenues à la position initiale. A 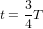 ,
, 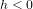 , donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à
, donc l’éloignement du centre des particules à 6h et 12h est négatif – elles se sont rapprochées du centre – et le rapprochement des particules à 3h et 9h est lui aussi négatif – elles s’en sont éloignées. L’ellipse à 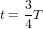 a la même forme que l’ellipse à
a la même forme que l’ellipse à 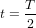 tournée de 90˚. A
tournée de 90˚. A 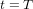 , les particules reviennent pour la deuxième fois à la position initiale.
, les particules reviennent pour la deuxième fois à la position initiale.

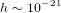 . Pour un détecteur avec une longueur
. Pour un détecteur avec une longueur 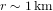 , cela correspond à une variation de longueur de l’ordre de
, cela correspond à une variation de longueur de l’ordre de 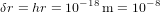 angström, où 1 angström est la taille caractéristique d’un atome. Mesurer une variation de longueur de cette taille correspond à mesurer une fluctuation de l’épaisseur d’un cheveu dans la distance entre le Soleil est l’étoile la plus proche, Proxima du Centaure. Des mesures d’une telle précision semblent impossibles. En fait, elles constituent un défi technologique majeur, mais elles ont été faites.
angström, où 1 angström est la taille caractéristique d’un atome. Mesurer une variation de longueur de cette taille correspond à mesurer une fluctuation de l’épaisseur d’un cheveu dans la distance entre le Soleil est l’étoile la plus proche, Proxima du Centaure. Des mesures d’une telle précision semblent impossibles. En fait, elles constituent un défi technologique majeur, mais elles ont été faites.

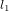 et
et 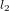 (Fig. 1).
(Fig. 1).
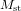 . Une partie de la lumière est réfléchie et redirigée vers le miroir
. Une partie de la lumière est réfléchie et redirigée vers le miroir 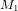 . Une autre partie continue son chemin en ligne droite vers le miroir
. Une autre partie continue son chemin en ligne droite vers le miroir 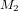 . La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers
. La lumière qui suit le premier chemin (la ligne rouge) est réfléchie vers 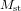 . Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers
. Une partie traverse le miroir semi-transparent et arrive au détecteur D. L'autre partie (la partie réfléchie) est perdue. La lumière qui suit le deuxième chemin (la ligne bleue) est elle aussi renvoyée vers 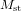 . Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.
. Dans le cas du chemin bleu, c'est la lumière réflechie par le miroir semi-transparent qui est envoyée au détecteur.

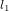 et
et 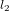 des deux chemins après leur séparation sont
des deux chemins après leur séparation sont 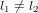 . Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins
. Dans l'exemple en Fig. 2, les ondes rouges et bleues, qui étaient parties de la source S avec la même phase (elles ont toutes commencé leur chemin au même point de la courbe sinusoïdale), arrivent au détecteur D avec des phases différentes parce qu'elles ont parcouru des chemins avec des longueurs différentes (en Fig. 2, la distance x le long des chemins 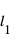 et
et 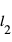 est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (
est mesurée à partir de la position x=0 du détecteur D en allant à rebours ; la longueur d’onde λ est utilisée comme unité de mesure).
Dans le cas de la courbe bleue continue, l'onde bleue et l'onde rouge arrivent au détecteur toutes les deux presque en phase de crête. L'interférence est constructive et amplifie le signal reçu (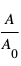 est le rapport entre l’amplitude
est le rapport entre l’amplitude 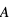 mesurée par le détecteur et l’amplitude
mesurée par le détecteur et l’amplitude 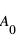 émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin
émise à la source).
Dans le cas de la courbe bleue à traits, une petite variation de la longeur du chemin 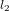 (5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
(5λ/16 dans le cas montré en figure) fait en sorte que l'onde bleue arrive en phase de vallée. L'interférence est alors destructive et l'amplitude de l'onde résultante est beaucoup plus faible. Une variation de 5/16 de longueur d’onde, qui n’est rien sur un chemin de plusieurs kilomètres, réduit l’amplitude du signal détecté d’un ordre de grandeur.
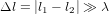 , où
, où  est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si
est la longueur d’onde de la lumière laser, mais ce n’est pas ça qui est important. Le principe est que, si 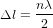 et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si
et n est un entier pair, alors les deux ondes arriverons en phase, leur interférence sera constructive et l’intensité lumineuse mesurée par le détecteur sera maximale, alors que, si 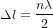 et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.
et l’entier n est impair, l’interférence sera destructive et l’intensité lumineuse mesurée sera nulle. Un interféromètre est donc un instrument capable de mesurer des variations du chemin optique égales à une fraction de la longueur d’onde λ de la lumière laser.

