Le sommeil agité de la matière
Dans la section précédente, nous avons considéré le mouvement d’une bille sur la surface d’un matelas, sur lequel on a déposé une balle de bowling, qui représente une grande masse, pensée comme statique. Remplaçons maintenant la balle de bowling par un être humain qui s’assoit sur le lit. Les êtres humains ont une différences majeure par rapport aux balles de bowling : ils bougent tout le temps. L’espace-temps est plus similaire à un matelas à ressorts. Quand la matière qui le déforme bouge, il propage des vibrations dans sa géométrie, c’est-à-dire dans les composantes de la métrique 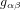 . C'est ça, les ondes gravitationnelles.
. C'est ça, les ondes gravitationnelles.
L’analogie avec les ondes électromagnétiques est évidente. Un courant qui varie avec le temps produit des ondes électromagnétiques - c’est, par ailleurs, comme ça qu’une antenne fonctionne. Une distribution de matière qui varie avec le temps produit des ondes gravitationnelles.
A la vitesse de la lumière
La similarité est aussi présente dans la vitesse de propagation, qui est la vitesse de la lumière dans les deux cas. La raison n’est pas difficile à comprendre si on considère le parcours historique qui a amené d'abord à la théorie de la relativité restreinte, puis à la théorie de la relativité générale. Nous allons résumer ce parcours brièvement.
Un peu d'histoire :
I. - La relativité galiléenne
Au début il y avait la mécanique et la théorie de la gravitation de Newton. En mécanique newtonienne, la vitesse est relative : le voyageur assis est au répos par rapport au wagon, il est un mouvement par rapport à un observateur sur le quai, qui regarde le train partir. Si un corps se déplace à la vitesse  pour un observateur O, il se déplacera à la vitesse :
pour un observateur O, il se déplacera à la vitesse :
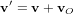
pour un autre observateur O', pour lequel O va à la vitesse 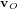 (l'´équation ci-dessus est connue comme la transformation de Galilée). En revanche, l'espace, le temps et l'accélération sont absolus, et la masse est constante. Donc la force
(l'´équation ci-dessus est connue comme la transformation de Galilée). En revanche, l'espace, le temps et l'accélération sont absolus, et la masse est constante. Donc la force 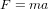 doit être la même dans tous les référentiel inertiels, dans lesquels il n'y a pas de forces apparentes.
doit être la même dans tous les référentiel inertiels, dans lesquels il n'y a pas de forces apparentes.
Cela est bien le cas pour la force gravitationnelle. Dans la théorie de la gravitation de Newton, la force 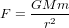 avec laquelle deux corps de masse M et m s'attirent ne dépend que de la distance r entre les deux corps, qui est indépendante du référentiel (le distance entre le passeger et son café est un mètre pour le passager et un mètre pour l'observateur sur le quai). Elle ne dépend pas de leur vitesses.
avec laquelle deux corps de masse M et m s'attirent ne dépend que de la distance r entre les deux corps, qui est indépendante du référentiel (le distance entre le passeger et son café est un mètre pour le passager et un mètre pour l'observateur sur le quai). Elle ne dépend pas de leur vitesses.
II. - Le magnétisme met en crise la relativité galiléenne
La crise de la mécanique classique commence avec la découverte du magnétisme, parce que les forces magnétiques dépendent des vitesses des charges. Une charge au répos ne produit pas de champs magnétique. Donc la présence (ou l'absence) de forces magnétiques devrait dépendre du référentiel, ce qui est incompatible avec la notion que la force est absolue.
Les physiciens de la fin du 19ème siècle se trouvaient donc dans une position très inconfortable. Soit ils abandonnaient les transformations de Galilée, soit ils acceptaient que les lois de l'électromagnétisme n'étaient pas vraies dans tous les référentiels, et alors la question était : quel est le référentiel privilegié, par rapport auquel les vitesses des charges doivent être mesurées ?
III. - Naissance et abandon de l'hypothèse de l'éther
L'hypothèse la plus répandue était celle de l'éther. Les ondes sonores ne voyagent pas dans le vide. Elles ont besoin d'un milieu matériel dans lequel se propager (l'air, l'eau, un mur). La même chose aurait pu valoir – on pensait – pour les ondes électromagnétiques. Voilà donc l'idée de l'éther, une substance très légère, très fine, qui remplit tout l'espace et qui fournit le milieu dans lequel les ondes électromagnétiques se propagent. Dans cette vision, l'éther définissait le référentiel privilégié par rapport auquel les vitesses des charges doivent être mesurées pour un calcul correct des forces électromagnétiques.
Einstein refuse la notion de cette substance indétectable. Les équations de l'électromagnétisme prédisent que la lumière doit avoir une vitesse c. Plutôt que chercher dans quel référentiel cette prédiction est vraie, Einstein suppose que les équations de l'électromagnétisme doivent être vraies pour tous les observateurs inertiels. Donc c est une constante fondamentale de la nature. Si les transformations de Galilée, pour lesquelles toute vitesse dépend du référentiel, sont en conflit avec cette conclusion, c'est eux qu'il faut changer. C'est comme ça que les transformations de Lorentz remplacent les transformations de Galilée.
IV. - Pourquoi une théorie relativiste de la gravitation ?
La théorie de la relativité restreinte remplace les lois de Newton par de nouvelles lois dynamiques invariantes par rapport aux transformations de Lorentz, qui ont donc l’avantage d’être entièrement compatibles avec la théorie électromagnétique. Mais cela laisse ouvert le problème de trouver une nouvelle théorie de la gravitation qui soit invariante par rapport aux transformations de Lorentz (les transformations qui préservent la vitesse de la lumière).
Ce problème est résolu avec la découverte de la théorie de la relativité générale. Les équations d’Einstein, qui donnent 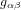 en fonction de la distribution de matière, ont donc été développées exprès de telle manière que la trajectoire d’un photon soit toujours décrite par l'équation :
en fonction de la distribution de matière, ont donc été développées exprès de telle manière que la trajectoire d’un photon soit toujours décrite par l'équation :
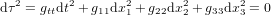 ,
,
qui se reduit à l'équation 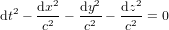 et donc à
et donc à 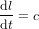 dans le cas sans gravité
dans le cas sans gravité 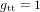 ,
, 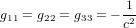 .
.
Constante fondamentales
La théorie de la relativité générale ne contient que deux constantes physiques : la vitesse de la lumière c et la constante de gravitation universelle G. Ensemble avec la constante de Planck h, qui définit l'échelle des phénomènes quantiques, elles constituent les trois constantes de la nature les plus fondamentales.
La constante de gravitation universelle G exprime l’intensité du couplage entre la matière et la géométrie : dans notre comparaison, elle détermine la masse par unité de surface que l’on doit déposer sur un matelas pour obtenir un enfoncement donné. G n’a pourtant aucun effet sur la propagation des ondes gravitationnelles dans le vide, c’est-à-dire, à grande distance des masses qui les ont générées.
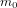 et vitesse
et vitesse 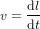 pour laquelle :
pour laquelle :
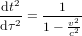 (1)
(1)
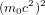 , d'une manière à obtenir :
, d'une manière à obtenir :
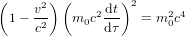 (2).
(2).
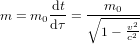 (3)
(3)
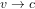 .
.
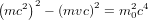 (4),
(4),
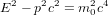 (5),
(5),
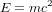
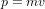
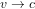 ,
, 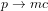 et donc
et donc 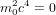 . Une particule qui se déplace a la vitesse de la lumière doit avoir une masse
. Une particule qui se déplace a la vitesse de la lumière doit avoir une masse 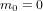 .
.