Il est désormais temps de l'utiliser, ce fameux oculaire. Commençons par le mettre à la sortie d'une lunette astronomique.
 La lunette astronomique
La lunette astronomique
Une lunette astronomique est constituée de deux lentilles :
- Une lentille objectif, en entrée de l'instrument, qui capte la lumière de l'astre et en fait l'image à son foyer.
- Une lentille oculaire, en sortie, qui, nous l'avons déjà vu, rejette l'image de l'astre à l'infini afin d'en faciliter son observation à l'oeil.
Dans le cas d'une lunette astronomique, les deux lentilles sont convergentes, et l'image de l'astre sera inversée.
La lunette astronomique
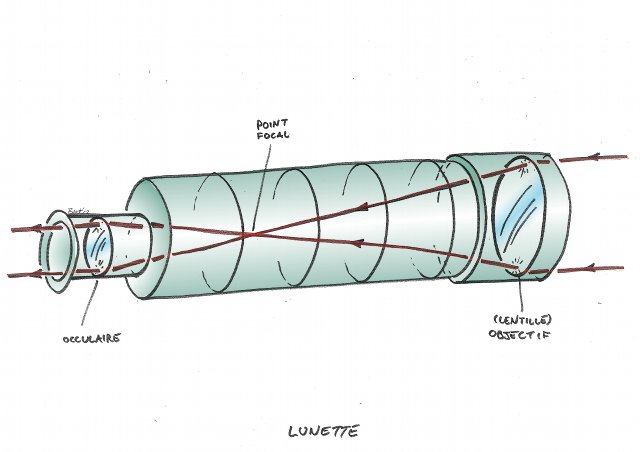
Une lunette est constituée de deux lentilles convergentes en entrée (objectif) et sortie (oculaire).
Crédit :
B. Mollier
 La lunette de Galilée
La lunette de Galilée
La lunette de Galilée se distingue par la nature de la lentille oculaire. Cette dernière est ici divergente. L'image en sortie sera droite.
À focale équivalente, la lunette de Galilée sera plus courte. Nous verrons pourquoi.
Lunette astronomique - Lunette de Galilée
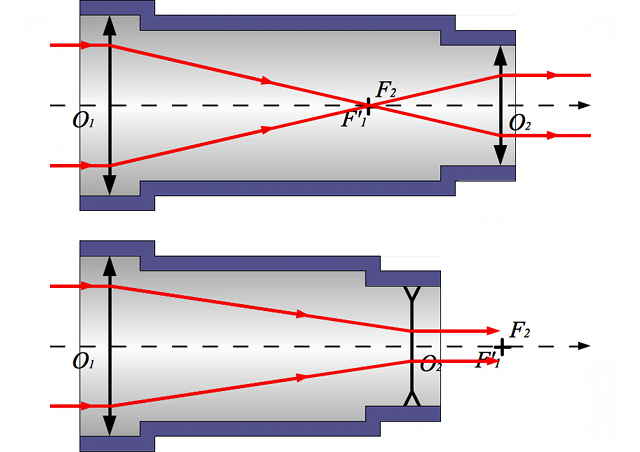
En haut, une lunette astronomique avec 2 lentilles convergentes. En bas, une lunette de Galilée avec un objectif convergent et un oculaire divergent.
Crédit :
ASM/B. Mollier
 L'objectif
L'objectif
L'objectif capte la lumière provenant de l'astre, et en fait l'image  à son foyer.
à son foyer.
Plus la focale de l'objectif sera grande, plus l'image sera également grande. Et si on se rappelle de la section sur l'appareil photo, on se souviendra que son angle de champ sera d'autant plus petit que cette focale est grande.
Principe de fonctionnement
Crédit :
ASM/B. Mollier
 L'oculaire
L'oculaire
L'image intermédiaire 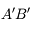 étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
Et si on fait appel au cours sur la loupe, on se souviendra que l'image finale 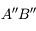 est d'autant plus grande que la focale de l'oculaire est courte.
est d'autant plus grande que la focale de l'oculaire est courte.
 Remarques
Remarques
- Compte-tenu de ce qu'on vient de dire, on sent bien que l'image de notre astre sera d'autant plus grosse que la focale de l'objectif est longue et celle de l'oculaire est courte. Le grossissement serait-il égal au rapport des deux focales ? La réponse page suivante.
- Le principe de fonctionnement est le même pour la lunette de Galilée. La seule différence étant que l'image intermédiaire
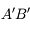 constitue un objet virtuel pour l'oculaire.
constitue un objet virtuel pour l'oculaire.
 Système afocal
Système afocal
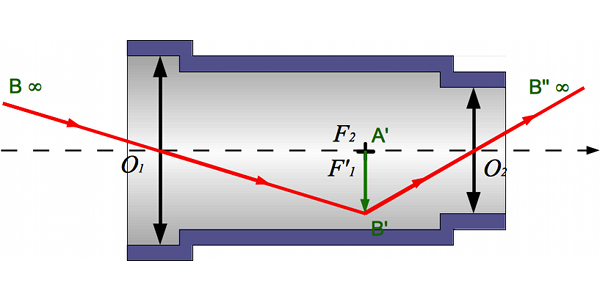
Dans une lunette (et, nous le verrons également, un télescope) l'objet est à l'infini et l'image aussi. Ce système n'a donc pas de foyer. Il est dit afocal.
Comment réaliser un tel système ? L'image intermédiaire est, par définition, au foyer principal image de l'objectif. Pour projeter l'image finale 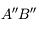 à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
Bref, pour fabriquer un système afocal, il suffit de superposer le foyer principal image de l'objectif avec le foyer principal objet de l'oculaire.
Nous allons calculer le grossissement d'une lunette astronomique en fonction des focales de son objectif et de son oculaire. Nous vérifierons ainsi si l'hypothèse émise à la page précédente est juste.
 Calcul du grossissement
Calcul du grossissement
Par définition de grossissement 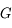
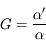
Il vient assez immédiatement que
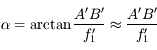 et
et 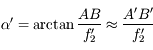
D'où 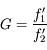
 Remarques
Remarques
L'image sera d'autant plus grande que la focale de l'objectif sera grande et celle de l'oculaire petite. On trouve bien le résultat qui était attendu.
Ce résultat est valable également pour la lunette de Galilée.
Grossissement
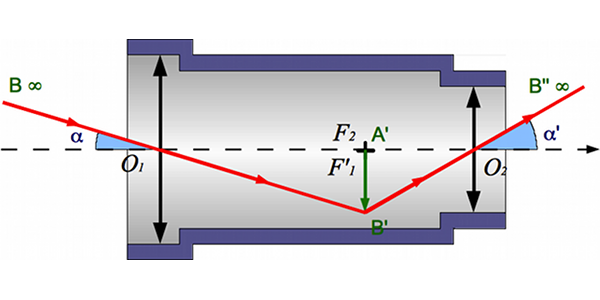
Le grossissement d'une lunette est égale au rapport des focales de l'objectif et de l'oculaire.
Crédit :
ASM/B. Mollier
Auteur: B. Mollier
 Observation de Jupiter
Observation de Jupiter
Difficulté : ☆☆
Temps : 20 min
On souhaite observer Jupiter à l'aide d'une lunette de 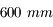 de focale (il s'agit ici de la focale de l'objectif).
de focale (il s'agit ici de la focale de l'objectif).
Jupiter

Jupiter, photographiée au télescope de
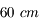
de la table équatoriale, à l'observatoire de Meudon. On y voit la grande tache rouge (bande rouge du haut), ainsi qu'une tempête (bande rouge du bas).
Crédit :
P. Kervella
Question 1)
Calculer le diamètre apparent de cette planète à l'opposition.
On parle d'opposition quand la planète est au plus proche de la Terre.
Le rayon équatorial de Jupiter est de 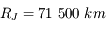 . À l'opposition, elle se situe à environ
. À l'opposition, elle se situe à environ 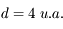 de la Terre.
de la Terre.
Question 2)
Vous disposez de 3 oculaires de 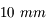 ,
, 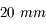 et
et 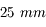 de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
Question 3)
Calculez alors le diamètre apparent de Jupiter dans cet oculaire.
Question 4)
La grande tache rouge mesure à peu près 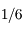 du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?
du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?
La résolution de l'oeil, c'est-à-dire la taille du plus petit détail visible, est de l'ordre de 1'.
Ce qui va suivre ne s'applique pas aux lunettes de Galilée.
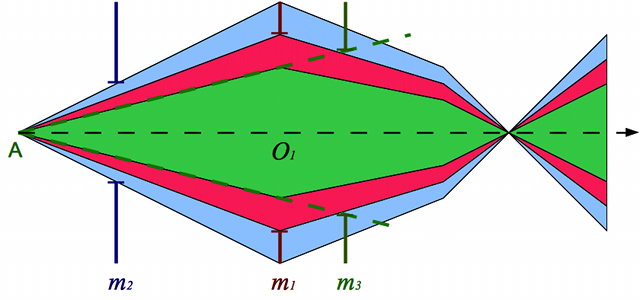
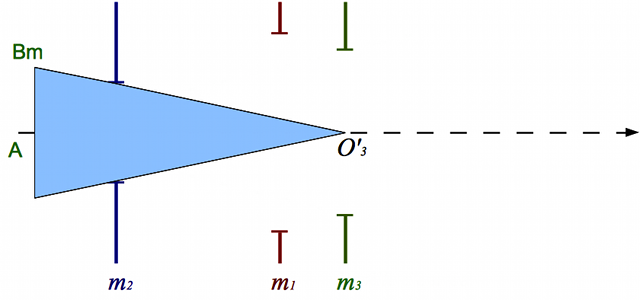
 Champ d'une lunette astronomique
Champ d'une lunette astronomique
Le champ de la lunette est l'ensemble des points de l'espace visibles dans l'instrument. Comme dans le cas de l'appareil photo, cet espace est un cône. Les objets à l'intérieur de celui-ci seront visibles, ceux à l'extérieur, non.
Grand champ

La grande coupole de l'observatoire de Meudon. Le champ de vue est grand ici.
Crédit :
B. Mollier
Champ réduit

La grande coupole de l'observatoire de Meudon. Le champ de vue est réduit.
Crédit :
B. Mollier
 Champ de l'oculaire
Champ de l'oculaire
L'image en sortie sera-t-elle petite ? (c'est-à-dire qu'on pourra l'embrasser en entier sans bouger l'oeil), ou au contraire sera-t-elle grande ? (il faudra alors bouger son oeil pour tout voir, ce qui n'est pas forcément agréable). C'est ce qu'on appellera le champ de l'oculaire.
Pour l'instant, nous ferons l'hypothèse que le champ de l'oculaire est celui de l'oeil, c'est-à-dire 50°.
Champ de l'oculaire réduit

Lorsque le champ de l'oculaire est réduit (inférieur à 50°), on peut voir toute l'image sans bouger l'oeil.
Crédit :
B. Mollier
Champ de l'oculaire grand

Lorsque le champ de l'oculaire est trop grand (supérieur à 50°) comme ici, on ne peut pas voir toute l'image sans bouger l'oeil. C'est fatiguant et peu agréable. (Cliquez sur l'image pour agrandir)
Crédit :
B. Mollier
 Remarques
Remarques
Le champ est inversement proportionnel au grossissement. Pour une lunette donnée, et donc une focale fixée, le champ diminue avec la focale de l'oculaire. Plus l'oculaire est court, plus le champ est réduit.
La démonstration de ce résultat est ici.
Le champ d'une lunette est limité par le diaphragme de champ
Champ d'une lunette
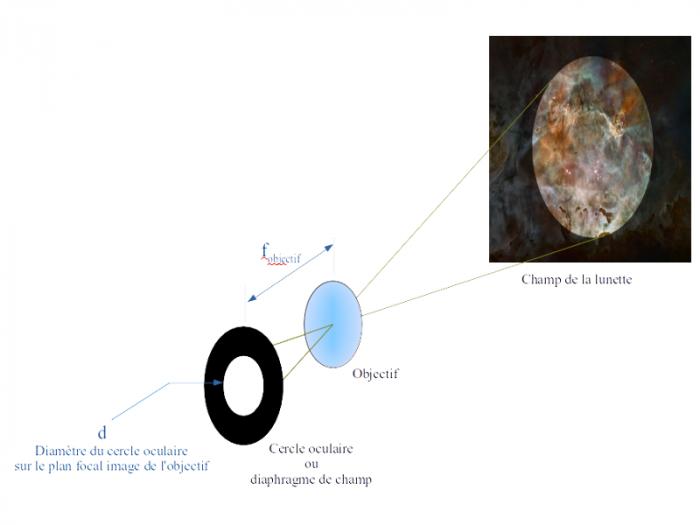
L'expression du champ d'une lunette est très proche de celle d'un appareil photographique : où d est le diamètre du diaphragme de champ, au niveau du plan focal image de l'objectif, f_objectif la distance focale image de l'objectif.
La démonstration de ce résultat est très simple, puisqu'il suffit d'écrire la définition de la tangente de l'angle
Auteur: B. Mollier
 Observation de la Lune
Observation de la Lune
Par une nuit de pleine Lune, on désire observer l'astre sélène. On possède une lunette de 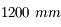 de focale, ainsi qu'un oculaire de
de focale, ainsi qu'un oculaire de 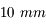 de focale et de
de focale et de 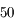 ° de champ.
° de champ.
Question 1)
Calculez le grossissement de cet instrument.
Question 2)
À partir du champ de l'oculaire, calculez l'angle de champ de la lunette. Pourra-t-on voir la Lune en entier dans l'oculaire ? Et la Galaxie d'Andromède (M31) ?
Le diamètre apparent de la Lune est de 0,5°. Celui de M31 est de 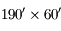 .
.
Dans les quelques pages à venir, nous allons rentrer dans des détails un peu plus techniques. Je les donne pour satisfaire la curiosité du lecteur, mais ils ne rentreront pas aux programmes de l'examen.
 Diaphragme d'ouverture
Diaphragme d'ouverture
Considérons un instrument possédant un certain nombre de lentilles. Faisons avec l'image d'un point 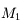 situé sur l'axe optique.
situé sur l'axe optique.
Diaphragme d'ouverture
La lentille
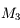
est celle qui limite le plus la taille du faisceau. Le faisceau rouge, prenant appui sur la monture
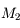
est vignété par

. Le faisceau bleu, prenant appui sur la monture
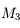
est vignété par
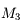
et
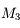
. La lentille
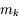
joue le rôle de diaphragme d'ouverture.
Crédit :
ASM/B. Mollier
Ce point émet un faisceau lumineux. Certains rayons de ce faisceau ressortiront de l'instrument, d'autres seront interceptés par la monture d'une des lentilles.
Pour connaître la quantité de lumière qui ressort de l'instrument, il faut chercher la monture qui limite la taille du faisceau (sur notre image, c'est la monture 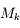 ).
).
On nommera cette monture diaphragme d'ouverture.
 Exemples de diaphragme d'ouverture
Exemples de diaphragme d'ouverture
Sur une lunette et un télescope, où on cherche à avoir le plus de lumière, on construit l'instrument de telle sorte que le diaphragme d'ouverture soit la première lentille (ou le miroir primaire). Comme c'est l'optique la plus grande, il serait dommage qu'elle ne serve à rien si c'est une autre monture plus petite qui joue le rôle de diaphragme d'ouverture.
En photographie, la problématique est différente. L'ouverture étant liée au temps de pose et à la profondeur de champ, on cherche à la contrôler en fonction de l'effet recherché. C'est donc un diaphragme physique, avec un diamètre ajustable, placé dans l'objectif, qui servira de diaphragme d'ouverture.
 Pupille d'entrée, pupille de sortie
Pupille d'entrée, pupille de sortie
Pour rechercher quelle monture limite la largeur de notre faisceau, une méthode consiste à rechercher l'antécédent de ces montures par rapport à toutes les précédentes.
Un rayon qui passera chacun des conjugués 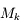 traversera toutes les montures réelles
traversera toutes les montures réelles 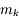 . Trouver le diaphragme d'ouverture
. Trouver le diaphragme d'ouverture 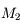 revient à chercher le conjugué
revient à chercher le conjugué 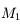 dont le diamètre est le plus petit.
dont le diamètre est le plus petit.
Pupille d'entrée
On cherche les antécédents des montures
à travers
et
à travers
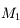
et
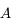
.
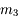
est son propre antécédent. On cherche ensuite lequel de ces antécédents limite le plus le faisceau issu de
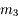
. Ici, c'est
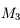
.
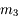
est appelé pupille d'entrée, et son image
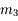
est appelée diaphragme d'ouverture.
Crédit :
ASM/B. Mollier
Ici, c'est 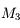 .
. 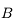 est appelé pupille d'entrée et
est appelé pupille d'entrée et 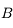 diaphragme d'ouverture.
diaphragme d'ouverture.
 Remarque
Remarque
La pupille d'entrée est le conjugué du diaphragme d'ouverture dans l'espace objet.
De la même manière, on définit la pupille de sortie comme étant le conjugué du diaphragme d'ouverture dans l'espace image.
Pour profiter pleinement d'un instrument, il faut que la pupille de sortie et la pupille de l'oeil soient confondues.
Ce n'est pas nécessairement une lentille qui joue le rôle de diaphragme d'ouverture. Ça peut-être un vrai diaphragme, comme dans le cas de l'appareil photo.
On peut également placer un vrai diaphragme physique, en entrée, pour jouer le rôle à la fois de diaphragme d'ouverture et de pupille d'entrée. (En effet, s'il est placé en amont de la première lentille, il est son propre antécédent).
 Dans ce pragraphe...
Dans ce pragraphe...
... je m'étendrai un peu plus sur la notion de champ d'une lunette, et j'introduirai les notions de diaphragme de champ et de lucarne.
 Diaphragme de champ
Diaphragme de champ
On considère cette fois-ci un point 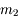 , hors de l'axe optique. Intéressons-nous au rayon issu de
, hors de l'axe optique. Intéressons-nous au rayon issu de 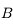 et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.
et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.
Diaphragme de champ
L'antécédent
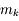
, appelé lucarne d'entrée, est celui qui limite le plus l'angle de champ.
Crédit :
ASM/B. Mollier
Faisons bouger 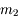 jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués
jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués 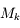 (ici
(ici 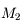 ).
).
Par définition, ce conjugué est appelé lucarne d'entrée, et son antécédent associé 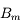 (ici
(ici 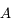 ) est appelé diaphragme de champ.
) est appelé diaphragme de champ.
 Champ moyen
Champ moyen
Le rayon touchant le bord du diaphragme de champ est noté 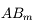 . Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre
. Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre 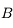 et de rayon
et de rayon 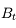 .
.
C'est grosso-modo la portion visible de l'image. (Mais pas tout à fait)
Champ moyen

Le cercle bleu représente le champ moyen. Il délimite à peu près la zone visible.
Crédit :
B. Mollier
Que voit-on réellement dans l'oculaire ?
 Champ de pleine lumière
Champ de pleine lumière
Considérons maintenant un autre du point 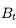 , de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.
, de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.
Champ pleine lumière
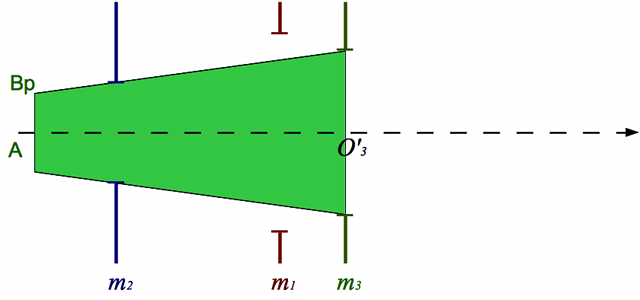
Le faisceau lumineux issu d'un point situé dans le champ pleine lumière passera la pupille d'entrée sans être vignété par la lucarne.
Crédit :
ASM/B. Mollier
Le faisceau lumineux issu d'un point situé dans le champ de pleine lumière passera la pupille d'entrée sans être vignété par la lucarne.
Le faisceau lumineux issu d'un point situé en dehors de ce champ sera en partie, voir totalement, vignété par la lucarne d'entrée. Au delà de ce cercle de pleine lumière, la luminosité commence à décroître.
Champ pleine lumière

Le cercle vert délimite le champ de pleine lumière. Au delà de ce cercle, la luminosité décroît.
Crédit :
B. Mollier
 Champ de contour
Champ de contour
La luminosité décroît jusqu'au cercle de diamètre 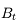 .
.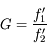 est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de
est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de 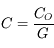 passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.
passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.
Champ de contour
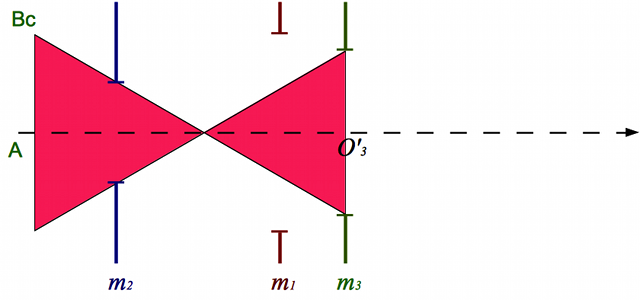
Tout objet situé en dehors de ce champ de contour sera invisible dans la lunette.
Crédit :
ASM/B. Mollier
Il délimite le champ de contour. Ce champ inclut les deux autres champs définis précédemment.
Pur résumer, dans le champ de pleine lumière, toute la lumière rentrant dans la lunette en ressort. En dehors du champ de contour, plus aucune lumière ne ressort de l'instrument. Entre les deux, une partie de la lumière entrante est stoppée quelque part dans la lunette.
Champ de contour

Le cercle rouge représente le champ de contour. Au delà de ce cercle, plus aucune lumière n'est visible.
Crédit :
B. Mollier
Les trois champs

En vert, le champ de pleine lumière, qui est inclus dans le champ moyen (en bleu) qui est inclus dans le champ de contour (en rouge).
Crédit :
B. Mollier
 Ce que l'on voit
Ce que l'on voit
Visuellement, on observe un cercle au bord flou, où la lumière décroît progressivement du centre vers le bord. Ce n'est pas agréable à l'oeil.
Le jeu consiste donc à confondre ces trois champs, afin d'obtenir un bord net. Il faut pour cela déplacer le diaphragme de champ de façon à ce que son conjugué, la lucarne d'entrée, soit dans le même plan que l'objet observé. Dans le cas d'un instrument astronomique, il faut que la lucarne d'entrée soit à l'infini.
Cercle oculaire flou

Ici, le cercle oculaire est flou, ce qui est désagréable à l'oeil. Les trois champs ne sont pas superposés. La lucarne d'entrée n'est pas dans le plan de l'objet (la coupole ici).
Crédit :
B. Mollier
Cercle oculaire net

Ici, le cercle oculaire est net, ce qui est plus agréable à l'oeil. Les trois champs se superposent. La lucarne d'entrée est dans le plan de l'objet (la coupole ici).
Crédit :
B. Mollier
 Description d'une lunette
Description d'une lunette
Une lunette est l'association de deux lentilles. Un objectif convergent et un oculaire convergent (lunette astronomique) ou divergent (lunette de Galilée).
 Système afocal
Système afocal
Une lunette est un système afocal, c'est-à-dire que le faisceau issu d'un objet à l'infini ne converge pas en sortie de l'instrument. C'est à l'oeil de faire l'image de cet objet. La lunette est un instrument subjectif.
Pour réaliser un système afocal, il faut superposer le foyer principal image de l'objectif avec le foyer principal objet de l'oculaire.
 Grossissement
Grossissement
Le grossissement d'une lunette est le rapport des focales de l'objectif et de l'oculaire,
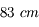
Le grossissement sera d'autant plus grand que la focale de la lunette est grande, et celle de l'oculaire réduite.
 Angle de champ
Angle de champ
L'angle de champ de la lunette est proportionnel à celui de l'oculaire (qui est en général de 40-50°) et inversement proportionnel au grossissement :
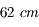
 Diaphragmes
Diaphragmes
Il existe deux types de diaphragmes :
- le diaphragme de champ, qui limite le champ de vue,
- le diaphragme d'ouverture, qui limite l'ouverture, c'est-à-dire la luminosité.
Auteur: B. Mollier
 La grande lunette de Meudon
La grande lunette de Meudon
La Grande coupole de l'observatoire de Meudon abrite une des plus grandes lunettes de la planète. Il s'agit en fait de deux lunettes montées en parallèle. L'une mesurant 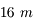 de diamètre, l'autre
de diamètre, l'autre 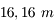 . Elles possèdent toutes deux une focale de
. Elles possèdent toutes deux une focale de 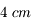 .
.
Grande lunette

La Grande Lunette de l'Observatoire de Meudon. Héliogravure de Dujardin publiée en 1896 dans les Annales de l'Observatoire d'Astronomie Physique de Paris, Sis Parc de Meudon - Volume 1 planche IX.
Crédit :
Observatoire de Paris
Question 1)
La lunette et son oculaire sont réglés de sorte à obtenir un système afocal. La focale de la lunette est de 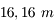 , celle de l'oculaire est de
, celle de l'oculaire est de 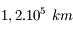 . Calculez le grossissement.
. Calculez le grossissement.
Question 2)
Quel est le diamètre apparent de Saturne, avec et sans ses anneaux, à l'opposition ? Quel sera alors son diamètre dans la lunette ?
Saturne est située à 10 u.a. du Soleil, et possède un diamètre de 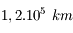 . Celui des anneaux est le double.
. Celui des anneaux est le double.
Question 3)
La division de Cassini est-elle visible à la lunette ?
La division de Cassini mesure 5000 km de large.
Question 4)
En supposant que l'angle de champ de l'oculaire est de 50°, calculez l'angle de champ de la lunette. Saturne est-elle visible en entier ?
Question 5)
Calculez l'ouverture de la lunette. Comparez cette valeur à celle des télescopes professionnels modernes.
Les télescopes modernes possèdent des ouvertures de l'ordre de 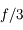 .
.
- Question 1
Solution :
Par définition du grossissement
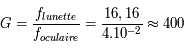
Le grossissement est de 400 !
- Question 2
Aide :
Saturne est située à 10 u.a. du Soleil, et possède un diamètre de 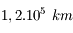 . Celui des anneaux est le double.
. Celui des anneaux est le double.
Solution :
À l'opposition, la distance Terre-Saturne est de 9 u.a. soit 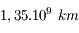 . On en déduit son angle apparent :
. On en déduit son angle apparent :
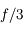
Le diamètre apparent de Saturne est de 18 secondes d'angle. Avec ses anneaux, elle mesure environ 36 secondes d'angle.
Dans la lunette, elle mesure alors 400 fois plus, soit 2 degrés.
- Question 3
Aide :
La division de Cassini mesure 5000 km de large.
Solution :
L'angle apparent de la division est de l'ordre de  . À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
. À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
- Question 4
Solution :
L'angle de champ de la lunette est de 0,13°. Saturne est visible en entier parce que sa taille fait 36 arcsec avec les anneaux. La planète est 13 fois plus petite que l'angle de champ de la lunette.
- Question 5
Aide :
Les télescopes modernes possèdent des ouvertures de l'ordre de 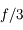 .
.
Solution :
Pour obtenir l'ouverture, on divise le diamètre de la lunette par sa focale. On obtient donc des ouvertures respectives de 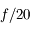 et
et  pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.
pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.
 La lunette astronomique
La lunette astronomique
 La lunette de Galilée
La lunette de Galilée
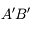 à son foyer.
à son foyer.

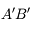 étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
étant en général petite, il faut la regarder avec une loupe : l'oculaire. Ce dernier grossit l'image et la rejette à l'infini.
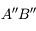 est d'autant plus grande que la focale de l'oculaire est courte.
est d'autant plus grande que la focale de l'oculaire est courte.
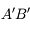 constitue un objet virtuel pour l'oculaire.
constitue un objet virtuel pour l'oculaire.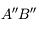 à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
à l'infini, nous avons placé le foyer principal objet sur l'image intermédiaire.
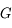
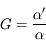
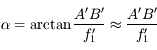 et
et 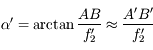
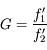
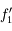 ) et de l'oculaire (
) et de l'oculaire (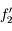 )
)
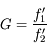

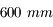 de focale (il s'agit ici de la focale de l'objectif).
de focale (il s'agit ici de la focale de l'objectif).

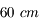 de la table équatoriale, à l'observatoire de Meudon. On y voit la grande tache rouge (bande rouge du haut), ainsi qu'une tempête (bande rouge du bas).
de la table équatoriale, à l'observatoire de Meudon. On y voit la grande tache rouge (bande rouge du haut), ainsi qu'une tempête (bande rouge du bas).
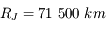 . À l'opposition, elle se situe à environ
. À l'opposition, elle se situe à environ 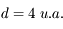 de la Terre.
de la Terre.
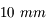 ,
, 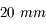 et
et 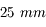 de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
de focale respectivement. Lequel devez-vous utiliser pour obtenir le meilleur grossissement ?
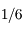 du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?
du diamètre de Jupiter. Sera-t-elle visible dans cet instrument ?




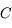 d'une lunette astronomique (et d'un télescope) est le rapport du champ de l'oculaire
d'une lunette astronomique (et d'un télescope) est le rapport du champ de l'oculaire 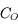 par le grossissement
par le grossissement 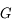 :
:
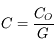

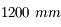 de focale, ainsi qu'un oculaire de
de focale, ainsi qu'un oculaire de 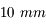 de focale et de
de focale et de 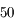 ° de champ.
° de champ.
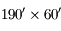 .
.
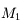 situé sur l'axe optique.
situé sur l'axe optique.

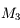 est celle qui limite le plus la taille du faisceau. Le faisceau rouge, prenant appui sur la monture
est celle qui limite le plus la taille du faisceau. Le faisceau rouge, prenant appui sur la monture 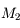 est vignété par
est vignété par  . Le faisceau bleu, prenant appui sur la monture
. Le faisceau bleu, prenant appui sur la monture 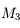 est vignété par
est vignété par 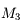 et
et 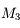 . La lentille
. La lentille 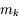 joue le rôle de diaphragme d'ouverture.
joue le rôle de diaphragme d'ouverture.
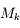 ).
).
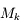 traversera toutes les montures réelles
traversera toutes les montures réelles 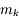 . Trouver le diaphragme d'ouverture
. Trouver le diaphragme d'ouverture 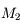 revient à chercher le conjugué
revient à chercher le conjugué 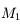 dont le diamètre est le plus petit.
dont le diamètre est le plus petit.

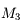 à travers
à travers 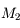 et
et 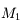 à travers
à travers 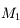 et
et 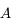 .
. 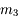 est son propre antécédent. On cherche ensuite lequel de ces antécédents limite le plus le faisceau issu de
est son propre antécédent. On cherche ensuite lequel de ces antécédents limite le plus le faisceau issu de 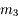 . Ici, c'est
. Ici, c'est 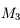 .
. 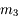 est appelé pupille d'entrée, et son image
est appelé pupille d'entrée, et son image 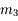 est appelée diaphragme d'ouverture.
est appelée diaphragme d'ouverture.
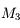 .
. 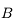 est appelé pupille d'entrée et
est appelé pupille d'entrée et 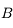 diaphragme d'ouverture.
diaphragme d'ouverture.
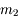 , hors de l'axe optique. Intéressons-nous au rayon issu de
, hors de l'axe optique. Intéressons-nous au rayon issu de 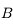 et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.
et passant par le centre de la pupille d'entrée et donc au centre du diaphragme d'ouverture et de la pupille de sortie. Il est appelé rayon moyen ou rayon principal.

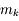 , appelé lucarne d'entrée, est celui qui limite le plus l'angle de champ.
, appelé lucarne d'entrée, est celui qui limite le plus l'angle de champ.
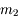 jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués
jusqu'à ce que le rayon rayon principal soit intercepté par un des conjugués 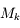 (ici
(ici 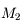 ).
).
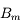 (ici
(ici 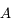 ) est appelé diaphragme de champ.
) est appelé diaphragme de champ.
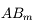 . Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre
. Il délimite le champ moyen de l'instrument. Le champ moyen est le disque de centre 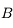 et de rayon
et de rayon 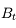 .
.

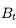 , de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.
, de telle sorte que le rayon qui en est issu passe par le bord de la lucarne d'entrée et la pupille d'entrée (en vert sur la figure). Il délimite également un champ, plus petit que le précédent appelé champ de pleine lumière.


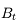 .
.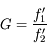 est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de
est un point particulier : les rayons qui en sont issus passent par le bord supérieur de la lucarne d'entrée puis par le bord inférieur de la pupille d'entrée. Bref, le faisceau issu de 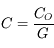 passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.
passant par les lucarne et pupille d'entrée se résume à un seul rayon lumineux.




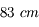
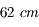
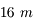 de diamètre, l'autre
de diamètre, l'autre 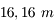 . Elles possèdent toutes deux une focale de
. Elles possèdent toutes deux une focale de 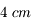 .
.

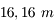 , celle de l'oculaire est de
, celle de l'oculaire est de 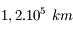 . Calculez le grossissement.
. Calculez le grossissement.
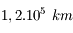 . Celui des anneaux est le double.
. Celui des anneaux est le double.
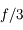 .
.

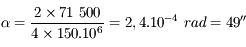
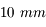 pour avoir le plus fort grossissement. Il sera alors de
pour avoir le plus fort grossissement. Il sera alors de 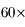 .
.
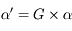 avec
avec 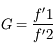
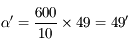
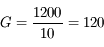
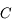 de la lunette est le champ de l'oculaire divisé par le grossissement. Il vaut donc
de la lunette est le champ de l'oculaire divisé par le grossissement. Il vaut donc 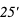
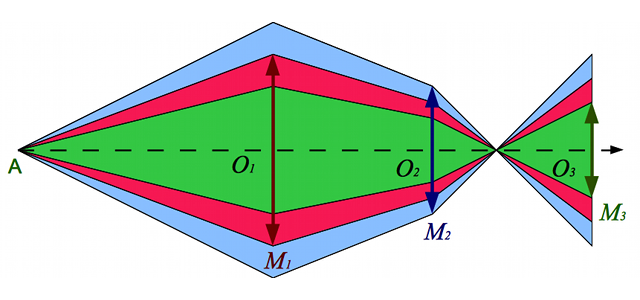
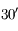 , elle ne sera pas visible en entier dans la lunette, il faudra préférer un oculaire de
, elle ne sera pas visible en entier dans la lunette, il faudra préférer un oculaire de 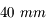 qui donnera un champs de
qui donnera un champs de 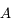 . M3 ne sera pas visible entierrement, même avec un oculaire de
. M3 ne sera pas visible entierrement, même avec un oculaire de 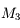 .
.
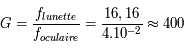
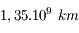 . On en déduit son angle apparent :
. On en déduit son angle apparent :
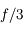
 . À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
. À la lunette, on la verra sous un angle de 5 minutes d'angle, ce qui largement au dessus de la résolution de l'oeil.
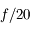 et
et  pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.
pour les deux lunettes. Ces lunettes sont très fermées en comparaison des télescopes de maintenant. Il faudra donc poser beaucoup plus longtemps pour obtenir la même quantité de photons issus d'un point de l'astre.