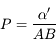Nous allons étudier, dans cette section, le système optique oeil + loupe. C'est, vous l'aurez reconnu, un doublet de deux lentilles convergentes.
Pourquoi étudier le système oeil + loupe ? Parce que tous les instruments d'optique subjectifs possèdent un oculaire, qui est équivalent à une loupe. Étudier ce système nous permettra de nous familiariser avec les notions de grossissement, de puissance, de netteté de l'image...
 Intérêt de la loupe
Intérêt de la loupe
Pour observer les détails d'un objet, il est nécessaire de le rapprocher le plus possible de notre oeil, au  . Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
. Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
Utiliser une lentille convergente, une loupe, va nous permettre d'obtenir une image de taille angulaire plus grande que l'objet. On grossit l'image !
De plus, en plaçant l'objet au foyer de la loupe, l'image est à l'infini. L'oeil n'a pas besoin d'accommoder et ne se fatigue plus.
 Intérêt de l'oculaire
Intérêt de l'oculaire
L'oculaire, qui est une sorte de loupe, permet de rendre subjectif l'objectif d'une lunette ou d'un télescope. Il renvoie l'image issue de ces derniers à l'infini, afin d'être vue par l'oeil, sans se fatiguer.
En fonction de leur focale, les oculaires permettent d'agrandir l'image de l'objet et de réduire ou d'augmenter l'angle de champ.
 Angle apparent
Angle apparent
L'oeil est sensible à l'angle apparent d'un objet. En effet, il ne fait pas la distinction entre un objet proche et petit et un objet grand et lointain. Certes, le cerveau y arrive en interprétant diverses informations, comme la vision en 3 dimensions, ainsi que le paysage dans son ensemble, mais fermez un oeil, vous verrez que c'est tout de suite moins évident.
L'autre exemple est celui de la Lune et du Soleil, qui n'ont pas la même taille, mais qui ont le même diamètre apparent.
Le but d'une loupe, d'un oculaire, puis des systèmes comme les lunettes et les télescopes, est d'augmenter l'angle apparent.
 Angle apparent d'un objet à l'infini
Angle apparent d'un objet à l'infini
Pour un objet à l'infini, l'angle apparent est directement l'angle sous lequel on voit l'objet. Pour mémoire, le diamètre apparent de la Lune et du Soleil est de 0,5°.
 Angle apparent d'un objet proche
Angle apparent d'un objet proche
S'il est proche, ce diamètre est donné par le rapport de sa taille par sa distance à l'oeil.
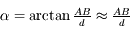
 Remarque
Remarque
Pour un objet proche, l'angle apparent dépend bien sûr de la distance à laquelle il se trouve.
 Utiliser une loupe
Utiliser une loupe
Je rappelle qu'une loupe est une lentille convergente. Pour fonctionner en "loupe", il faut placer l'objet entre le foyer principal objet et la lentille.
 Construction de l'image
Construction de l'image
Construisons l'image d'un objet à travers une loupe.
Image à travers une loupe
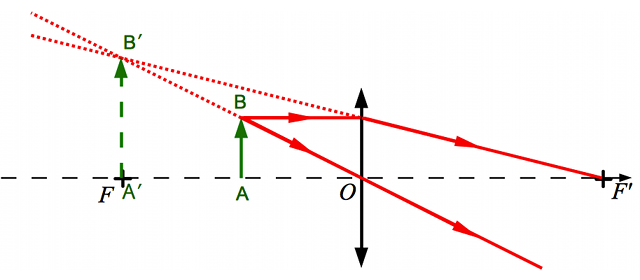
Crédit :
ASM/B. Mollier
 Angle apparent de l'image
Angle apparent de l'image
L'image est plus grosse et plus éloignée. Quel est alors son angle apparent ?
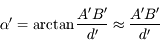
Cet angle dépend de la distance entre la loupe et l'objet, ainsi que de la loupe et l'oeil.
 Cas limite : l'objet est au foyer
Cas limite : l'objet est au foyer
Plaçons nous plutôt dans le cas le plus reposant pour l'oeil (ainsi que le plus simple mathématiquement) : l'image rejetée à l'infini. Pour cela, il suffit de placer le foyer principal objet sur l'objet qu'on veut observer.
Objet au foyer
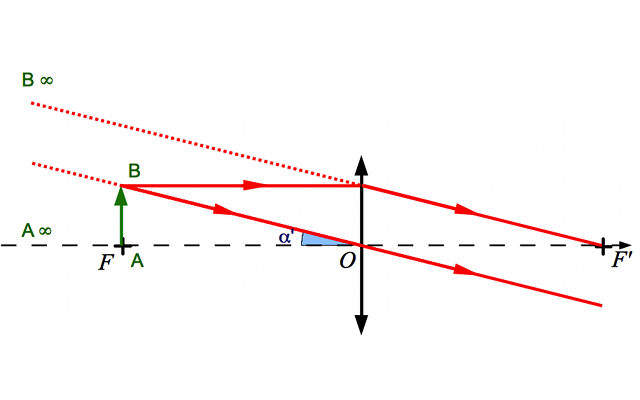
L'objet est placé au foyer, l'image est à l'infini.
Crédit :
ASM/B. Mollier
L'expression de l'angle apparent est alors immédiate
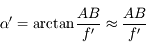
L'angle apparent dépend maintenant de la distance focale de la loupe, et uniquement de celle-ci. Plus cette distance est courte, plus grand sera l'angle apparent. On aimerait dire que, plus la loupe est convergente, plus elle grossit notre image. Mais que veut vraiment dire grossir ?
 Le grossissement
Le grossissement
On a à notre disposition deux diamètres apparents, l'un avec, l'autre sans la loupe (ou l'instrument subjectif en général).
On peut définir naturellement le grossissement 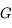 comme étant le rapport de ces deux quantités :
comme étant le rapport de ces deux quantités :
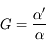
Plus un instrument est grossissant (c'est-à-dire plus 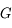 est grand) plus grand sera le diamètre apparent de l'image.
est grand) plus grand sera le diamètre apparent de l'image.
Grossissement d'un objet à l'infini
Le grossissement est le rapport de l'angle apparent de l'image sur l'angle apparent de l'objet.
Crédit :
ASM/B. Mollier
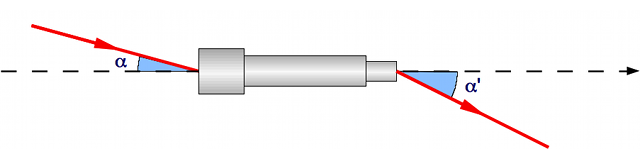
Grossissement d'un objet à distance finie
Le grossissement est le rapport de l'angle apparent de l'image sur l'angle apparent de l'objet.
Crédit :
ASM/B. Mollier
 Attention
Attention
Ne pas confondre grossissement et grandissement !
 Position du problème
Position du problème
Petit problème : pour un objet à distance 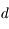 finie, le diamètre apparent
finie, le diamètre apparent 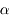 dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
Le microscope ou la loupe sont des exemples de système optique grossissant des objets à distance finie.
 La puissance
La puissance
On définit également, pour le cas des objets à distance finie, la puissance de l'instrument, comme étant le rapport de diamètre apparent de l'image, sur la taille 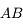 de l'objet :
de l'objet :
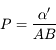
 Remarques
Remarques
Remarquons que 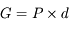
En astronomie, la distance 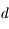 tend vers l'infini. La puissance est donc toujours nulle.
tend vers l'infini. La puissance est donc toujours nulle.
Si l'image est à l'infini, donc l'objet au foyer principal objet, la puissance est simplement la vergence de l'instrument : 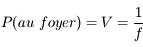
De nombreux instruments sont équipés d'oculaires : télescopes, lunettes, microscopes...
Cet instrument comprend plusieurs lentilles, mais joue le rôle d'une loupe. Il est cependant plus puissant, corrige les aberrations optiques et chromatiques, possède un champ plus grand. Il peut parfois être équipé d'un réticule pour mesurer des tailles angulaires, des parallaxes ou viser...
 La loupe
La loupe
Une loupe est une lentille convergente. Elle sert à grossir les objets. Une utilisation optimale consiste à placer son foyer sur l'objet visé. Son image est alors rejetée à l'infini. L'oeil n'a pas besoin d'accommoder et se fatigue moins.
 Le grossissement
Le grossissement
Le grossissement est le rapport de l'angle apparent de l'image sur celui de l'objet :
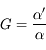
 La puissance
La puissance
On a également défini la puissance 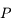 comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.
comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.
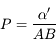
 Intérêt de la loupe
Intérêt de la loupe . Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
. Cependant, cela entraîne une fatigue de l'oeil, et, avec l'âge, ce point s'éloigne.
 Intérêt de l'oculaire
Intérêt de l'oculaire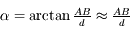
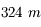 et est distante de
et est distante de 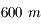 de l'esplanade.
de l'esplanade.
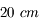 pour obtenir le même angle apparent ?
pour obtenir le même angle apparent ?

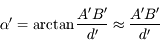

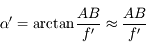
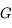 comme étant le rapport de ces deux quantités :
comme étant le rapport de ces deux quantités :
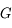 est grand) plus grand sera le diamètre apparent de l'image.
est grand) plus grand sera le diamètre apparent de l'image.


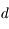 finie, le diamètre apparent
finie, le diamètre apparent 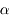 dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
dépend de la position de l'oeil. Or il serait bon d'avoir un grossissement ne dépendant que de l'instrument. Cela nous permettra de les comparer entre eux.
 , c'est-à-dire à 25 cm de l'oeil.
, c'est-à-dire à 25 cm de l'oeil.
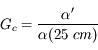 avec
avec 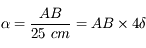
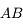 de l'objet :
de l'objet :
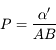
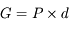
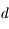 tend vers l'infini. La puissance est donc toujours nulle.
tend vers l'infini. La puissance est donc toujours nulle.
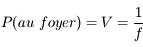
 et le
et le  pour être vue nette. Sa distance est comprise entre
pour être vue nette. Sa distance est comprise entre 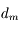 et
et 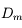 .
.
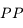 et du
et du 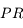 par loupe. Elle dépend bien sûr de la position de l'oeil par rapport à la loupe.
par loupe. Elle dépend bien sûr de la position de l'oeil par rapport à la loupe.
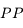 et
et 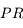 vaut respectivement :
vaut respectivement :
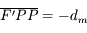 et
et 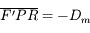 .
.
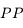 et
et 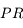 sont respectivement :
sont respectivement :
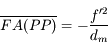 et
et 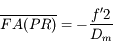
![= [-\frac{f'^2}{d_m}-f',-\frac{f'^2}{D_m}-f']](../pages_instruments-oculaire/equations_instruments-oculaire/equation35.png)
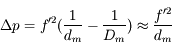
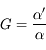
 comme étant le cas particulier du grossissement d'un objet situé à
comme étant le cas particulier du grossissement d'un objet situé à 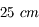 de l'oeil.
de l'oeil.
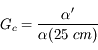
 comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.
comme étant le rapport entre la taille de l'objet et le diamètre apparent de l'image.