Les lois de Kepler
Auteur: Jean-Eudes Arlot
- Introduction
- L'héliocentrisme
- Pourquoi l'héliocentrisme ?
- Histoire : de la Terre plate aux orbites elliptiques
- Histoire : le monde d'Aristote
- Histoire : les premières mesures
- Histoire : l'univers de Ptolémée
- Histoire : l'héliocentrisme de Copernic
- Histoire : le géohéliocentrisme de Tycho-Brahe
- Histoire : les orbites elliptiques autour du soleil
- QCM
- Les trois lois de Kepler
- La première loi de Kepler
- La deuxième loi de Kepler
- La troisième loi de Kepler
- Exercice
- Exercice
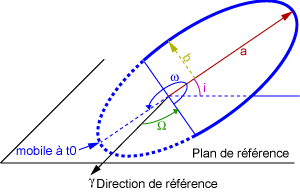
- En savoir plus: les paramètres de l'ellipse
- Les distances dans le système solaire
- Parallaxe diurne, parallaxe horizontale
- La troisième loi de Képler
- La distance Terre-Mars
- La distance Terre-Vénus
- QCM
Introduction
 Introduction
Introduction
L'observation du ciel n'est pas suffisante pour bien appréhender les distances des astres et comprendre le mécanisme de leur mouvement. L'observation va permettre de valider les principes théoriques qui ne seront tout d'abord que des suppositions. Les lois que Kepler va énoncer seront validées par l'observation.
L'héliocentrisme
Pourquoi l'héliocentrisme ?
Jusqu'à Copernic et Galilée, on suppose la Terre immobile au centre de l'univers. Effectivement, aucune observation ne peut mettre en évidence un mouvement de la Terre dans l'espace. Copernic et Galilée vont supposer le mouvement des planètes autour du Soleil. Kepler va énoncer des lois pour ce mouvement, lois qui ne découlent que de l'observation du mouvement des astres. Ces lois ne représentent qu'une description cinématique de ce mouvement sans faire d'hypothèses sur la nature des forces en jeu.
Kepler (1571-1630) est le disciple de Tycho Brahe (1546-1601) auquel il succède comme astronome de l'empereur d'Allemagne Rodolphe II. Tycho Brahe est principalement un observateur de positions précises mais s'il effectue de très bonnes observations, en revanche, il n'est pas convaincu par les théories héliocentriques de Copernic (1473-1543). Il pense toujours que la Terre est au centre du système solaire. Kepler va utiliser les observations de Tycho Brahe pour énoncer ses lois. Kepler est convaincu que Copernic a raison, ce qui sera définitivement admis après Galilée (1564-1642) en 1610 grâce à l'utilisation d'une lunette astronomique et à l'observation des satellites de Jupiter.
Kepler énonce ses deux premières lois en 1609 et sa troisième loi en 1619.

Kepler (1571-1630)
Crédit :
Danielle Briot - Collection particulière
Histoire : de la Terre plate aux orbites elliptiques
Il a fallu plus de deux mille ans pour comprendre que les planètes avaient des orbites elliptiques autour du Soleil. La progression des connaissances ne fut pas régulière, loin de là !
On doit la première démarche scientifique de recherche d'une représentation de l'univers à Thalès (625-547 avant J.-C.). Il fonda, au 6ème siècle avant notre ère, l'école des philosophes ioniens à Milet. La Terre était alors supposée de forme géométrique plate. L'un des disciples de Thalès, Anaximandre (610-547 avant J.-C.), supposa une Terre cylindrique habitée sur sa partie supérieure plane. C'est à cette époque que la notion de sphères célestes supportant les corps célestes apparaît : cette notion perdurera jusqu'au Moyen Âge.
Vers la même époque, à l'école de Pythagore (570-480 avant J.-C.) on affirma la sphéricité de la Terre, celle du Soleil et de la Lune en étant un indice. Toutes les formes et les mouvements célestes se devaient d'être parfaits, donc sphériques ou circulaires : le philosophe pythagoricien Parménide (543-449 avant J.-C.) fut le premier à exprimer la sphéricité de la Terre ainsi que le fait que la Lune était éclairée par le Soleil..
Le monde selon Philolaos (470-400 avant J.-C.)
Crédit : ASM/Damien Guillaume
Histoire : le monde d'Aristote
Aristote (384-322 avant J.-C.), disciple de Platon, précepteur d'Alexandre le Grand, peut sans doute être considéré comme le plus grand savant de l'Antiquité. Son oeuvre colossale, composée de plusieurs dizaines de volumes, abordera aussi bien l'astronomie, la physique que la botanique ou la médecine. Aristote va en particulier développer un modèle physique, fondé sur l'observation et la perception intuitive des phénomènes, dont l'influence sera déterminante pour les siècles à venir. Sa conception de l'Univers est basée sur 3 dogmes fondamentaux :
- la Terre est immobile au centre de l'Univers
- il y a séparation absolue ente le monde terrestre imparfait et changeant et le monde céleste parfait et éternel (la limite étant l'orbite de la Lune)
- les seuls mouvements célestes possibles sont les mouvements circulaires uniformes.
La Terre immobile est faite des quatre éléments eau, air, terre et feu. Aristote pense même avoir "démontré" l'immobilité de la Terre avec un argument basé sur le fait que si la Terre était en mouvement nous devrions en ressentir directement les effets. Pour ce qui est de la mécanique céleste, Aristote considérera un système de sphères centrées sur la Terre. La sphère extérieure est celle des fixes. Ce système présentait cependant un défaut majeur, qui sera mis en évidence au siècle suivant. S'il rendait en effet compte à peu près correctement des mouvements des planètes, il ne pouvait expliquer leurs variations d'éclat au cours de l'année, car dans ce modèle les planètes étaient supposées à une distance constante de la Terre. Certes, Aristote aurait pu invoquer une variation intrinsèque de l'éclat des planètes, mais cela était incompatible avec son dogme sur la perfection et l'immuabilité des cieux.
Le monde d'Aristote
Le système d’Aristote
Crédit : ASM/Damien Guillaume
Histoire : les premières mesures
Il semble qu'au 4ème siècle avant notre ère, Héraclide du Pont (388-310 avant J.-C.) envisagea que la sphère des fixes était immobile et que la Terre tournait autour de son axe, ce qui expliquerait le mouvement diurne des étoiles (mais les sources écrites sont ici très ténues et incertaines).
Au 3ème siècle avant notre ère Eratosthène (284-192 avant J.-C.) fit la première mesure précise du rayon terrestre : il utilisa le fait que l'ombre portée d'un bâton à midi faisait 7° 10' le jour du solstice à Alexandrie alors qu'elle était nulle (le Soleil était au zénith) 800 kilomètres plus au sud à Syène sur le tropique du Cancer. Ce fut le premier calcul mathématique de mesure dans le système solaire. Il trouva ainsi 6500 kilomètres pour le rayon terrestre, soit une valeur remarquablement correcte.
A la même époque vécut Aristarque de Samos (310-230 avant J.-C.), dont l'œuvre est attestée par très peu de traces écrites. Il fut sans doute un des premiers à estimer (avec une remarquable précision) la distance Terre-Lune. Aristarque est par ailleurs crédité pour avoir proposé un modèle héliocentrique du monde (mais le seul témoignage écrit est une phrase d'un manuscrit d'Archimède).
Au 2ème siècle avant notre ère vécut Hipparque (190-120 avant J.-C.), peut-être le plus grand astronome de l'Antiquité. Hipparque fut avant tout un grand observateur. Il mis en évidence le phénomène de précession des équinoxes, qu'il estima être de 36 secondes d'arc par an (la vraie valeur est de 50 secondes). Hipparque calcula également assez précisément la longueur de l'année tropique : 365 jours 5 heures 55 minutes 12 secondes (la vraie valeur était 365 jours 5 heures 48 minutes 46 secondes).
Histoire : l'univers de Ptolémée
L'astronomie grecque va connaître son apogée au 2ème siècle de notre ère avec l'astronome alexandrin Claude Ptolémée (100-170). Ptolémée va faire la synthèse de tous les travaux de ses prédécesseurs (en particulier Hipparque) et va les parachever en proposant un système physique et mathématique du ciel qui restera incontesté pendant près de 14 siècles. Tous les travaux astronomiques de Ptolémée sont quasiment regroupés dans un seul ouvrage majeur, la "grande syntaxe mathématique", plus connu sous le nom que lui donnèrent les Arabes : l'Almageste. L'Almageste reprend dans ses grandes lignes la vision aristotélicienne du monde physique, avec les mêmes dogmes et principes : dichotomie Terre/Univers, immobilité de la Terre, etc.
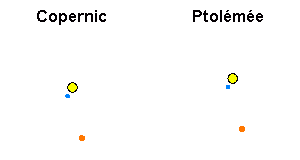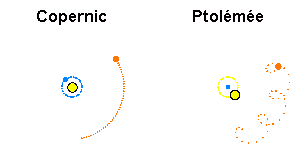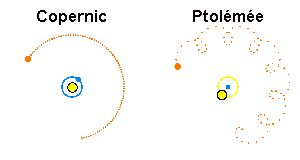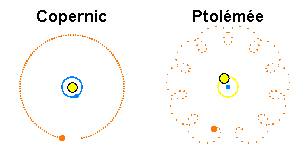
Crédit : ASM/Benoît Mosser
Histoire : l'héliocentrisme de Copernic
Nicolas Copernic (1473-1543), un chanoine et astronome polonais, va remettre en cause le modèle géocentrique du monde de Ptolémée et d'Aristote dans un ouvrage publié l'année de sa mort : le "De Revolutionibus orbium caelestium". Cet ouvrage propose un modèle héliocentrique du monde, dans lequel tous les mouvements planétaires sont centrés sur le Soleil. Mais surtout, ce que Copernic va affirmer c'est que la Terre n'est ni immobile, ni au centre du monde. Elle est en effet animée de 2 mouvements : l'un sur elle-même en 24h (qui remplace le mouvement de la sphère des fixes des Grecs anciens) et l'autre autour du Soleil en un an, faisant de la Terre une planète comme les autres. Contrairement à ce que l'on croit parfois, Copernic ne va pas démontrer l'héliocentrisme, car il faudra attendre plus de 150 ans pour avoir une preuve du mouvement de la Terre. L'argument de Copernic est que son modèle est plus simple, plus logique et plus "harmonieux" que celui de Ptolémée (même si dans le détail le fonctionnement mathématique du système copernicien est assez complexe).
Le De Revolutionibus, malgré son côté fondamentalement révolutionnaire, fut reçu avec relativement d'indifférence par les savants de l'époque.
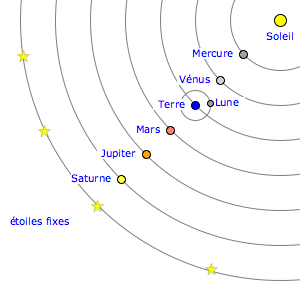
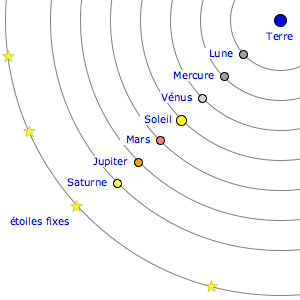
Le système héliocentrique de Copernic
Crédit : ASM/Damien Guillaume
Histoire : le géohéliocentrisme de Tycho-Brahe
Tycho Brahe (1546-1601) fut avant tout un observateur hors pair. Il construisit ses instruments lui permettant d'atteindre une précision de mesure inégalée (2 minutes de degré). Il effectua des observations continues du Soleil, de la Lune, des planètes et des étoiles pendant trente ans et constata les erreurs des tables d'éphémérides de l'époque. Il observa la supernova de 1572 ce qui sera le point de départ de la remise en cause de l'immuabilité de la sphère des fixes d'Aristote et de Ptolémée. Il observa une comète en 1577 et, là aussi, il prit en défaut les théories d'Aristote : la comète n'appartenait pas au monde sublunaire et son orbite coupait celles des autres planètes. Il ne put mesurer de parallaxe annuelle des étoiles, ce qui lui fit adopter le système géohéliocentrique.
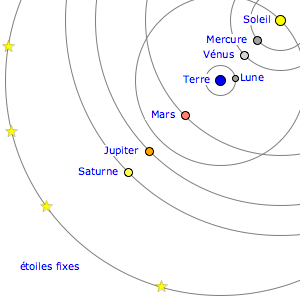
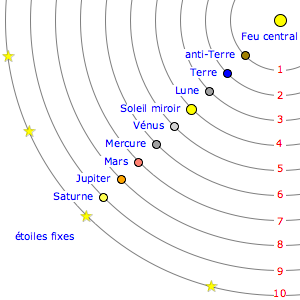
Le système de Tycho Brahe
Crédit : ASM/Damien Guillaume
Giordano Bruno (1548-1600) était plus un philosophe qu'un astronome mais il introduisit une vision du monde fondée sur un univers infini qui tranchait avec les idées admises alors. Il défendit aussi l'idée de la pluralité des mondes habités autour des étoiles et celle que la Terre n'était pas le centre de l'univers, pas plus que le Soleil. Il se heurta à l'Inquisition, ce qui n'était pas prudent à l'époque.
Histoire : les orbites elliptiques autour du soleil
Johannes Kepler (1571-1630), très grand calculateur et mathématicien, eut la chance de prendre la suite de Tycho Brahe dont il analysa les observations. Kepler fut capable d'en déduire les orbites des planètes et d'énoncer les lois qui portent son nom et qui caractérisent ces orbites. Il introduisit pour la première fois la notion d'orbite elliptique, rompant avec les sacro-saints mouvements circulaires uniformes érigés en dogme par les Grecs. Kepler montra par ailleurs que les plans des orbites planétaires passaient par le Soleil et non par la Terre, ce qui contredisait un des postulats du géocentrisme.
Galilée (1564-1642) était d'abord un physicien et il étudia la mécanique et la dynamique des corps en mouvement. Galilée établit la loi de l'inertie (tout corps non soumis à une force extérieure est animé d'un mouvement rectiligne uniforme et se trouve dans un référentiel que l'on nomme aujourd'hui "galiléen"). C'est à la fin de l'année 1609 et au début de 1610 qu'il a l'idée de braquer une lunette d'approche récemment inventée et qu'il a construit lui-même vers le ciel. Ses découvertes seront nombreuses et vont bouleverser la vision de l'univers de l'époque. Il observa des taches sur le Soleil, des cratères sur la Lune, les phases de Vénus, une multitude d'étoiles dans la Voie lactée et des satellites autour de Jupiter. Cette dernière découverte donnait le coup de grâce au géocentrisme. Il adhéra aux idées de Copernic et à l'héliocentrisme sans pouvoir le démontrer et ne considéra pas le géohéliocentrisme qui nous semble aujourd'hui être une étape incontournable dans l'élaboration d'un modèle d'univers.

Crédit :
Danielle Briot - Collection particulière
Ainsi, au début du XVIIème siècle, on avait une vision de l'univers assez proche de la réalité. Cependant, on ignorait complètement comment les mouvements observés pouvaient se faire. Il faudra attendre Newton et la gravitation
universelle et la mécanique céleste pour pouvoir décrire tous ces mouvements par des théories dynamiques et non plus de simples modèles cinématiques.
QCM
Les trois lois de Kepler
La première loi de Kepler
Chaque planète décrit, dans le sens direct, une ellipse dont le Soleil occupe l'un des foyers.
Jusqu'alors, on n'avait considéré que le cercle comme trajectoire possible des corps célestes. Ce sont les observations précises de Tycho Brahe qui ont permis de revenir sur ce postulat. L'ellipticité des orbites des planètes est très faible. La différence entre le cercle et l'orbite de la Terre est infime : si on veut la représenter sur une feuille de papier, la différence entre le cercle et l'ellipse tient dans l'épaisseur du trait de crayon ! Heureusement le Soleil n'est pas au centre de l'ellipse, mais au foyer qui est décentré.
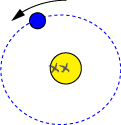
Orbite de la Terre : une ellipse peu excentrique dont le Soleil occupe un des foyers.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
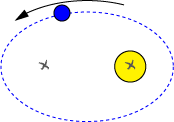
Cas d'une orbite très excentrique
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
La deuxième loi de Kepler
Les aires décrites par le rayon vecteur planète-Soleil sont proportionnelles aux temps employés pour les décrire.
La signification de cette loi est claire : les planètes ne tournent pas avec une vitesse uniforme ; elles vont plus vite quand elles sont près du Soleil et plus lentement quand elles en sont loin. Cela est particulièrement observable pour les comètes dont les orbites sont, contrairement à celles des planètes, très excentriques (très allongées).

La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales.
Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.
Crédit : ASM/Benoît Mosser
La troisième loi de Kepler
Le cube du demi grand axe "a" d'une orbite d'une planète, divisé par le carré de la période de révolution sidérale "T" est une constante pour toutes les planètes du système solaire.
C'est-à-dire :
a3/T2 = constante
ou bien n2 a3 = constante
(n étant le moyen mouvement = 2π/T)
Cette loi relie les planètes entre elles. En fait, cette loi provient de la masse prépondérante du Soleil dans le système solaire. On verra que la loi de la gravitation engendre une force proportionnelle aux masses en jeu. Dans le cas du système solaire, les masses des planètes sont négligeables devant celle du Soleil et la constante ci-dessus est le produit de la masse solaire et de la constante de la gravitation.
Kepler ne pouvait pas démontrer ses lois : il lui manquait les principes fondamentaux de la mécanique ainsi que la loi de Newton, c'est-à-dire les fondements de la dynamique, qui, appliqués aux astres, forment la mécanique céleste. Kepler introduit la notion de trajectoire elliptique qui va complètement modifier la modélisation du système solaire.
Exercice
 Calcul du demi grand axe d'Uranus
Calcul du demi grand axe d'Uranus
Question 1)
Calculer le demi-grand axe de l'orbite d'Uranus connaissant les paramètres de l'orbite terrestre et sachant que la période de révolution d'Uranus autour du Soleil est de 84 ans.
Appliquer la troisième loi de Kepler pour des corps tournant autour du Soleil
Exercice
 Distance minimale Terre-Saturne
Distance minimale Terre-Saturne
Question 1)
Calculez la distance minimale Terre-Saturne
connaissant la période orbitale de Saturne (29,5 ans). On
supposera les orbites dans le système solaire circulaires.
1 unité astronomique égale (environ): 150 millions de km,
c'est le demi grand axe de la Terre
sa période de révolution est un an
Calculer tout d'abord le demi-grand axe de Saturne
En savoir plus: les paramètres de l'ellipse
Les distances dans le système solaire
Parallaxe diurne, parallaxe horizontale
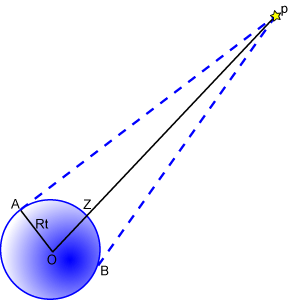
On a vu précédemment que triangulation ou parallaxe utilisait le même principe pour déterminer la distance d'un objet éloigné sans avoir à y aller et sans mesurer directement la distance à l'objet. On remarque que la précision de la mesure dépend de la longueur de la base. Il faut pouvoir mesurer les angles avec suffisamment de précision. Pour un astre pas trop éloigné, il suffit de se déplacer sur la surface de la Terre -ou mieux de faire deux observations simultanées à partir de deux lieux éloignés sur la surface de la Terre- pour en déterminer la distance.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
La parallaxe diurne a une valeur maximale : c'est la "parallaxe horizontale" pour un astre donné (quand l'observateur est en A). Elle sera atteinte pour un astre observé à l'horizon. Cette valeur est donc l'angle sous lequel un observateur situé sur l'astre P en question voit le rayon terrestre RT. La parallaxe diurne est nulle lorsque l'astre observé est au zénith (observateur en Z, sur la droite OP).
La troisième loi de Képler
Ayant vu comment les astronomes mesurent les distances aux astres lointains -mais pas trop-, comment va-t-on concrètement mesurer le système solaire tout entier ? Le Soleil est bien trop loin pour qu'une mesure de parallaxe nous en donne sa distance. Les lois de Kepler vont nous donner les rapports des distances des planètes au Soleil et il suffira de connaître une seule distance entre les planètes pour les connaître toutes.
La première loi de Kepler énonce que les orbites des planètes autour du Soleil sont des ellipses.
La deuxième loi de Kepler est la loi des aires. Plus simplement, elle indique les planètes vont plus vite sur leur orbite quand elles sont près du Soleil. Nous utiliserons cette loi pour l'analyse des observations de passage qui nécessite de connaître la vitesse angulaire apparente de Vénus sur le disque solaire.
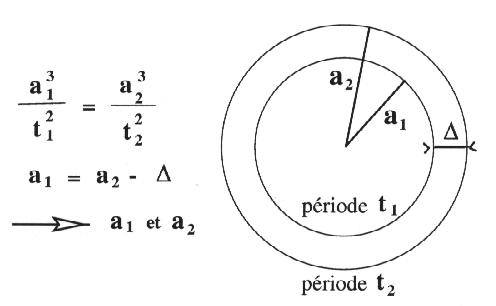
La troisième loi de Kepler nous fournit les rapports entre les distances au Soleil de toutes les planètes et il suffit ainsi de connaître une seule distance dans le système solaire pour connaître toutes les autres. Elle s'énonce ainsi :
le rapport a3/T2 est constant pour toutes les planètes du système solaire où a est le demi grand axe de l'orbite et T la période de révolution autour du Soleil. La figure ci-dessous montre ce qui se passe si les orbites sont des cercles, connaissant la distance Δ et les périodes t1 et t2.
La première loi de Kepler énonce le fait que les orbites sont des ellipses et on ne pourra donc pas assimiler les distances Soleil-Terre et Soleil-Vénus aux demi-grands axes aT et aV des orbites de la Terre et de Vénus. On passe du demi grand axe "a" à la distance Soleil-planète (rayon vecteur) "rP" par la formule :
rP = a (1 - e cos E) où e est l'excentricité de l'ellipse et E caractérise l'emplacement de la planète sur son orbite elliptique (E est appelé "anomalie excentrique").
La distance Terre-Mars
Pour mesurer le système solaire, il nous suffit donc de mesurer une distance entre la Terre et la planète la plus proche. Dès le XVIIème siècle, on s'est tourné vers Mars et Vénus qui passent régulièrement à une distance pas trop grande de la Terre.
Pour comprendre comment mesurer leur distance à la Terre, voyons concrètement comment en déterminer la parallaxe.
On a vu qu'il fallait mesurer un angle de visée d'un astre par rapport à une direction fixe, connue des deux observateurs, même éloignés et sans contact. Cette direction fixe va être fournie par un astre situé à proximité de l'astre dont on veut mesurer la distance, mais situé suffisamment loin pour pouvoir être considéré comme étant à l'infini. Cela revient à dire que sa parallaxe est nulle : quel que soit le lieu de la Terre d'où on l'observe, on le voit toujours dans la même direction. On va donc utiliser les étoiles pour lesquelles la parallaxe diurne est négligeable. On a appliqué cette méthode à la planète Mars dès le XVIIème siècle mais la visée des étoiles était difficile et on a cherché un autre astre et une méthode plus facile.
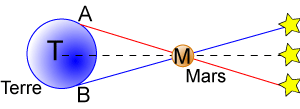
Cas de la planète Mars : celle-ci n'apparaît pas devant les mêmes étoiles selon le lieu d'observation sur Terre
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Pour la planète Mars, seul le principe de la parallaxe avec un calcul utilisant une base connue (dépendant des lieux d'observation sur Terre) va nous permettre de calculer la distance Terre Mars.
La distance Terre-Vénus
La planète Vénus, passant régulièrement devant le Soleil, a apporté une bonne solution. Lors d'un tel passage, le disque solaire est un repère sur lequel la planète Vénus va apparaître à des endroits différents pour des observateurs différents. C'est le principe de la parallaxe.
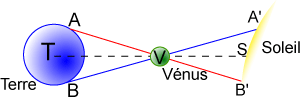
Cas de la planète Vénus : la projection de son disque sombre sur le disque solaire lors d'un passage n'est pas la même pour deux observateurs terrestres
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Pour Vénus, on se sert du Soleil comme référence pour calculer la parallaxe. A la différence du calcul de la parallaxe pour la planète Mars, le Soleil n'est pas à l'infini : il a lui aussi une parallaxe et il nous faut connaître le rapport des distances du Soleil à Vénus et à la Terre. Cela nous est fourni par les lois de Kepler. On connaît la distance AB, l'angle en V (par l'observation) ainsi que le rapport VA/VA' (par la troisième loi de Kepler), on en déduit VT, VS et TS, d'où la distance Terre-Soleil et l'unité astronomique. Le problème se complique du fait que A et B bouge (rotation de la Terre autour de son axe), ainsi que T et V (révolution de la Terre et de Vénus autour du Soleil).
Dès le XVIIIème siècle, la distance Terre-Soleil était connue assez précisément : 150 millions de kilomètres environ que l’on nommera l’unité astronomique, unité de mesure du système solaire.
QCM
Réponses aux QCM
pages_heliocentrisme/mctc-qcm-kepler.html
QCM
- Question 1
Solution : réponse 2)
(
oui, les instruments de mesure ne permettaient pas de détecter un mouvement de la Terre
)
Solution : réponse 3)
(
oui, le géocentrisme de Ptolémée permettait de prévoir la plupart des phénomènes célestes
)
- Question 2
Solution : réponse 2)
(
oui, sans l'ellipticité des orbites des planètes, l'héliocentrisme ne fonctionne pas bien
)
Solution : réponse 3)
(
oui, mais seulement par son utilisation de la lunette, parce que ce sont surtout les lois de Kepler qui ont bouleversé notre perception du système solaire
)
pages_distances-systeme/mctc-qcm-distances.html
QCM
- Question 1
Solution : réponse 1)
(
c'est suffisant mais ce n'est pas nécessaire...
)
Solution : réponse 3)
(
oui, la troisième loi de Kepler permet de calculer toutes les autres distances
)
- Question 2
Solution : réponse 2)
(
oui, c'est la distance Terre-Soleil
)
- Question 3
Solution : réponse 1)
(
oui, plus il est près de la Terre, plus sa direction dans le ciel change quand l'observateur se déplace
)
Réponses aux exercices
pages_kepler/mctc-demi-grand-axe.html
Exercice
'Calcul du demi grand axe d'Uranus'
pages_kepler/mctc-distance-terre-saturne.html
Exercice
'Distance minimale Terre-Saturne'
- Question 1
Aide :
1 unité astronomique égale (environ): 150 millions de km,
c'est le demi grand axe de la Terre
sa période de révolution est un an
Aide :
Calculer tout d'abord le demi-grand axe de Saturne
 Introduction
Introduction









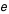 telle que
telle que 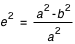 où
où 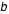 est le demi-petit axe
est le demi-petit axe 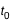 ou l'anomalie moyenne
ou l'anomalie moyenne 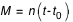 où
où 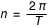 avec
avec 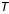 période de révolution définie par la 3ème loi de Kepler (qui dit que
période de révolution définie par la 3ème loi de Kepler (qui dit que 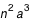 est une constante connue).
est une constante connue).