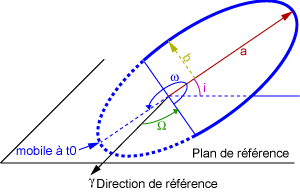
Chaque planète décrit, dans le sens direct, une ellipse dont le Soleil occupe l'un des foyers.
Jusqu'alors, on n'avait considéré que le cercle comme trajectoire possible des corps célestes. Ce sont les observations précises de Tycho Brahe qui ont permis de revenir sur ce postulat. L'ellipticité des orbites des planètes est très faible. La différence entre le cercle et l'orbite de la Terre est infime : si on veut la représenter sur une feuille de papier, la différence entre le cercle et l'ellipse tient dans l'épaisseur du trait de crayon ! Heureusement le Soleil n'est pas au centre de l'ellipse, mais au foyer qui est décentré.
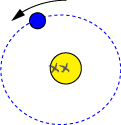
Orbite de la Terre : une ellipse peu excentrique dont le Soleil occupe un des foyers.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
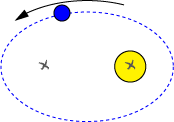
Cas d'une orbite très excentrique
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
Les aires décrites par le rayon vecteur planète-Soleil sont proportionnelles aux temps employés pour les décrire.
La signification de cette loi est claire : les planètes ne tournent pas avec une vitesse uniforme ; elles vont plus vite quand elles sont près du Soleil et plus lentement quand elles en sont loin. Cela est particulièrement observable pour les comètes dont les orbites sont, contrairement à celles des planètes, très excentriques (très allongées).

La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales.
Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.
Crédit : ASM/Benoît Mosser
Le cube du demi grand axe "a" d'une orbite d'une planète, divisé par le carré de la période de révolution sidérale "T" est une constante pour toutes les planètes du système solaire.
C'est-à-dire :
a3/T2 = constante
ou bien n2 a3 = constante
(n étant le moyen mouvement = 2π/T)
Cette loi relie les planètes entre elles. En fait, cette loi provient de la masse prépondérante du Soleil dans le système solaire. On verra que la loi de la gravitation engendre une force proportionnelle aux masses en jeu. Dans le cas du système solaire, les masses des planètes sont négligeables devant celle du Soleil et la constante ci-dessus est le produit de la masse solaire et de la constante de la gravitation.
Kepler ne pouvait pas démontrer ses lois : il lui manquait les principes fondamentaux de la mécanique ainsi que la loi de Newton, c'est-à-dire les fondements de la dynamique, qui, appliqués aux astres, forment la mécanique céleste. Kepler introduit la notion de trajectoire elliptique qui va complètement modifier la modélisation du système solaire.



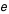 telle que
telle que 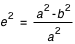 où
où 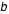 est le demi-petit axe
est le demi-petit axe 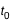 ou l'anomalie moyenne
ou l'anomalie moyenne 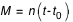 où
où 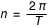 avec
avec 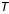 période de révolution définie par la 3ème loi de Kepler (qui dit que
période de révolution définie par la 3ème loi de Kepler (qui dit que 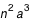 est une constante connue).
est une constante connue).