Traçons l'image d'un objet à travers une lentille convergente
On dispose d'un objet 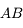 en amont de la lentille et du foyer objet. On cherche à tracer son image à travers la lentille.
en amont de la lentille et du foyer objet. On cherche à tracer son image à travers la lentille.
- On trace le rayon issu de
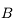 et passant par
et passant par 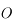 . Il n'est pas dévié.
. Il n'est pas dévié. - Il faut un deuxième rayon pour obtenir l'image de
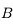 . En effet, dans les conditions de stigmatisme approché, deux rayons suffisent à définir un point image. On a le choix entre deux autres rayons. On trace par exemple le rayon issu de
. En effet, dans les conditions de stigmatisme approché, deux rayons suffisent à définir un point image. On a le choix entre deux autres rayons. On trace par exemple le rayon issu de 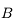 et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image
et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image 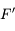 . Il croise le premier rayon en
. Il croise le premier rayon en 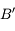 , image de
, image de 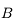 par la lentille.
par la lentille. - Par acquis de conscience, traçons un troisième rayon, et vérifions qu'il passe bien par
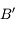 . Traçons le rayon issu de
. Traçons le rayon issu de 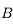 et passant par le foyer principal objet
et passant par le foyer principal objet 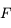 . Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point
. Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point 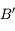 .
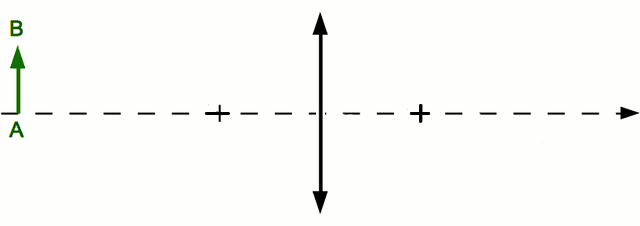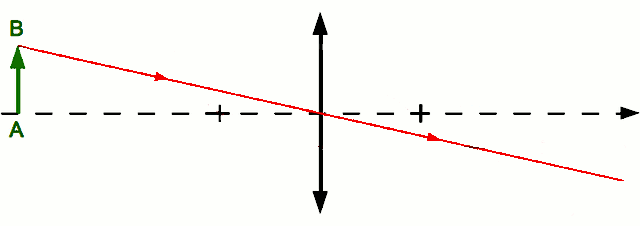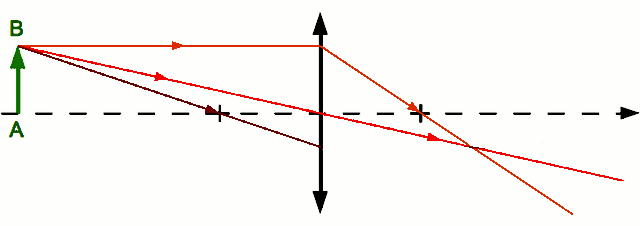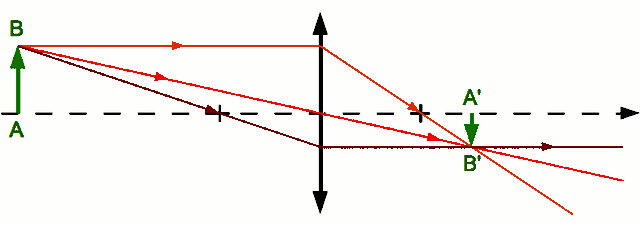
. - Il nous reste à tracer l'image
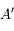 du point
du point 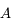 . On ne peut utiliser la même méthode que le point
. On ne peut utiliser la même méthode que le point 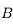 car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors ? Utilisons la propriété d'aplanétisme. On sait que
car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors ? Utilisons la propriété d'aplanétisme. On sait que 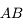 est perpendiculaire à l'axe optique. L'image
est perpendiculaire à l'axe optique. L'image 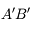 l'est également.
l'est également. 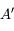 est donc le point de l'axe optique à la verticale de
est donc le point de l'axe optique à la verticale de 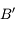 . Le tour est joué.
. Le tour est joué.
 Remarques
Remarques
- L'image
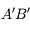 est inversée. On retrouve le deuxième cas décrit dans l'exemple décrit précédemment.
est inversée. On retrouve le deuxième cas décrit dans l'exemple décrit précédemment. - L'image
 est réelle car en aval de la lentille.
est réelle car en aval de la lentille.
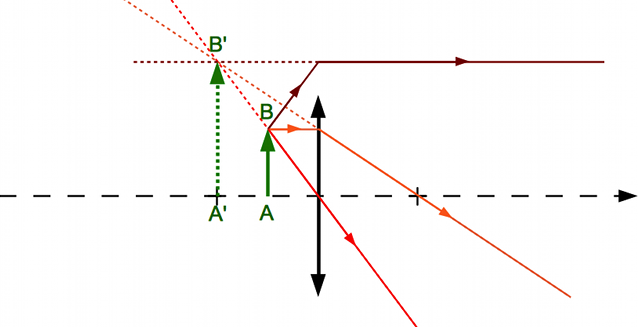
 est dans le même sens.
est dans le même sens. est virtuelle car en amont de la lentille.
est virtuelle car en amont de la lentille.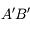 est plus grande que l'objet. On a affaire à une loupe.
est plus grande que l'objet. On a affaire à une loupe.
 est :
est :
 est :
est :
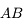 à l'infini. Il possédera un diamètre apparent
à l'infini. Il possédera un diamètre apparent 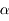 .
.
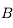 et passant par
et passant par 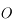 . Il n'est pas dévié.
. Il n'est pas dévié. sont parallèles les uns aux autres. Nous pouvons cependant tracer le rayon parallèle au premier passant par le foyer objet. Il ressortira parallèle à l'axe optique. On constate qu'il coupe le premier dans le plan focal. C'est normal. Nous avons défini le plan focal image comme ceci.
sont parallèles les uns aux autres. Nous pouvons cependant tracer le rayon parallèle au premier passant par le foyer objet. Il ressortira parallèle à l'axe optique. On constate qu'il coupe le premier dans le plan focal. C'est normal. Nous avons défini le plan focal image comme ceci.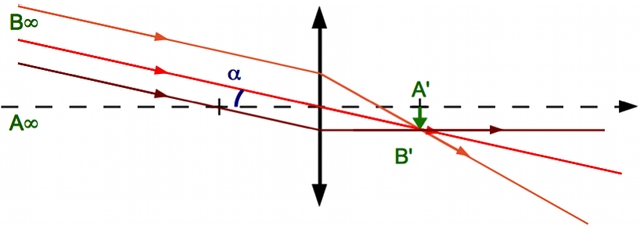
 et passant par
et passant par 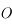 . Il n'est toujours pas dévié.
. Il n'est toujours pas dévié.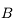 et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image
et parallèle à l'axe optique. Il ressort de la lentille en passant par le foyer principal image 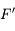 . Mais ce foyer est en amont de la lentille.
. Mais ce foyer est en amont de la lentille.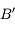 . Traçons le rayon issu de
. Traçons le rayon issu de 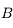 et passant par le foyer principal objet
et passant par le foyer principal objet 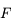 . Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point
. Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point 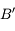
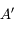 du point
du point 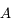 . On ne peut utiliser la même méthode que le point
. On ne peut utiliser la même méthode que le point 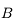 car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors. Utilisons la propriété d'aplanétisme. On sait que
car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors. Utilisons la propriété d'aplanétisme. On sait que 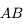 est perpendiculaire à l'axe optique. L'image
est perpendiculaire à l'axe optique. L'image 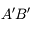 l'est également.
l'est également. 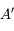 est donc le point de l'axe optique à la verticale de
est donc le point de l'axe optique à la verticale de 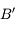 .
.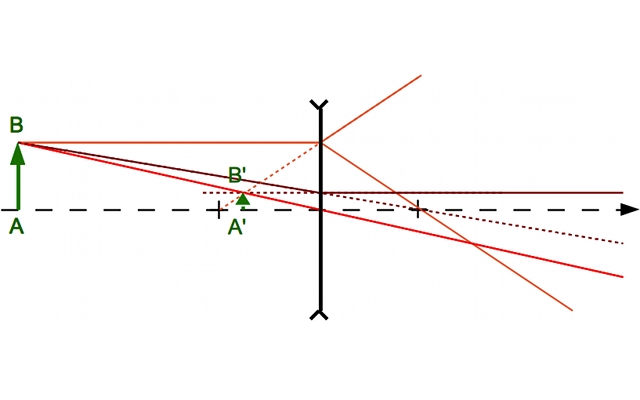
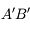 est :
est :
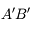 est :
est :
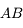 et d'une lentille divergente. Trouvez le tracé correct.
et d'une lentille divergente. Trouvez le tracé correct.