Ne vous inquiétez pas, on ne va pas être obligé de systématiquement tracer toutes nos images dès qu'on voudra obtenir la moindre position ou taille. Il existe des relations simples, nommées relations de conjugaison, permettant d'accéder à toutes ces données, connaissant uniquement la distance focale de la lentille.
Nous allons les démontrer à partir des constructions précédentes.
Crédit :
B. Mollier
Nous avons vu que la taille de l'image n'est pas nécessairement la même que celle de l'objet. Et celle-ci varie en fonction de la distance de l'objet et de la distance focale.
 Grandissement
Grandissement
Nous allons appeler grandissement le rapport des tailles de l'objet et de l'image.
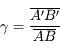
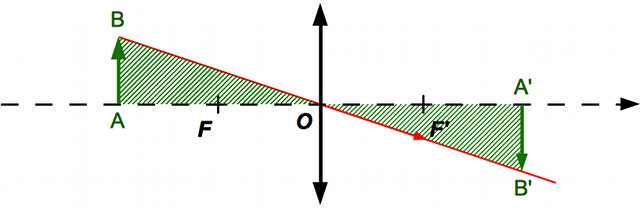
Crédit :
B. Mollier
En appliquant le théorème de Thalès, on trouve immédiatement que :
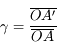
 Remarque
Remarque
Connaissant la distance de l'objet et de l'image, il est donc possible de calculer la taille de l'image.
Si le grandissement est positif, alors l'objet et l'image sont dans le même sens ; s'il est négatif, l'image est inversée par rapport à l'objet.
Si le grandissement est supérieur à 1, ou inférieur à -1, alors l'image est plus grande que l'objet. S'il est compris entre -1 et 1, l'image sera plus petite.
Auteur: B. Mollier
 Quelques grandissements
Quelques grandissements
Difficulté : ☆
Temps : 5 min
Voici 3 constructions géométriques :
Construction 1
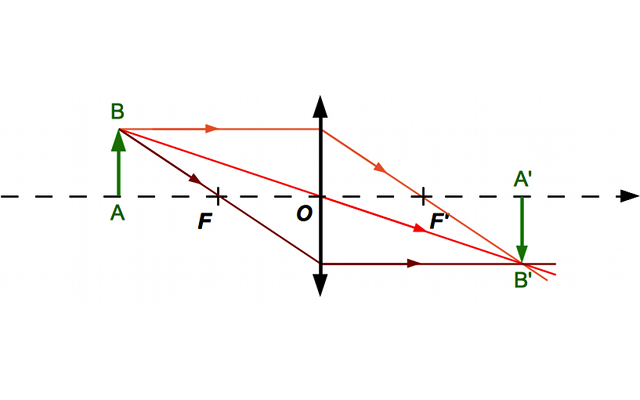
Crédit :
ASM/B. Mollier
Construction 2
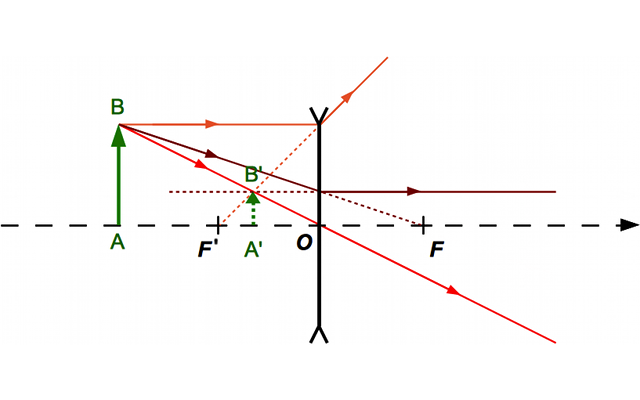
Crédit :
ASM/B. Mollier
Construction 3
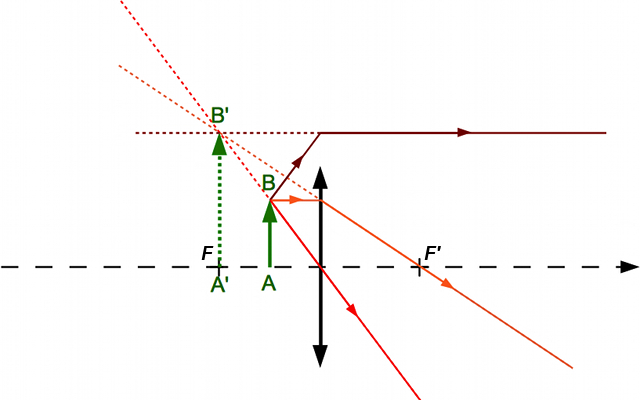
Crédit :
ASM/B. Mollier
Question 1)
Calculez le grandissement dans les trois cas.
Prenez les mesures sur les dessins.
 Grandissement : origines aux foyers
Grandissement : origines aux foyers
Et si on ne connaît pas la position de l'image ? Nous allons utiliser les foyers. En appliquant cette fois-ci le théorème de Thalès deux fois de chaque côté de la lentille, on obtient :
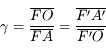
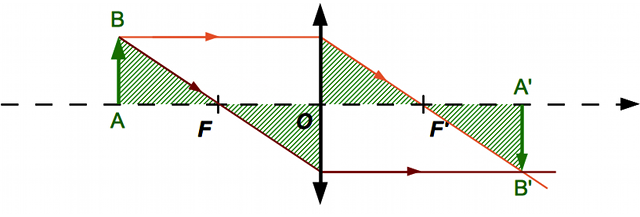
Crédit :
ASM/B. Mollier
Et voilà, connaissant la distance focale et la distance de l'objet, on peut calculer le grandissement.
 Relation de conjugaison de Newton (origines aux foyers)
Relation de conjugaison de Newton (origines aux foyers)
Remarquons qu'à partir de ces deux formules, on va pouvoir calculer la distance de l'image.
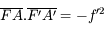
Nous venons d'établir la relation de conjugaison de Newton. Elle est aussi appelée relation de conjugaison avec origine au foyer, car les distances de l'objet et de l'image sont comptées à partir des foyers principaux.
Auteur: B. Mollier
 Quelques grandissements (2)
Quelques grandissements (2)
Difficulté : ☆
Temps : 5 min
On reprend les mêmes et on recommence !
Construction 1

Crédit :
ASM/B. Mollier
Construction 2

Crédit :
ASM/B. Mollier
Construction 3

Crédit :
ASM/B. Mollier
Question 1)
Sachant que la distance focale est de 4 cm en valeur absolue dans les 3 cas, retrouvez les valeurs de grandissement précédemment établies.
Pour ceux qui aurait la flemme de mesurer les distances 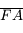 sur les figures,
sur les figures,
Auteur: B. Mollier
 Formule de Newton
Formule de Newton
On considère une lentille convergente de vergence 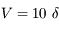 . On place un objet à une distance
. On place un objet à une distance 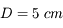 en amont du centre de la lentille.
en amont du centre de la lentille.
Question 1)
Calculez la position de l'image.
Calculez la distance focale image à partir de la vergence. Calculez la distance 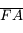 en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
Question 2)
Est-elle réelle ou virtuelle ?
Question 3)
Calculez sa taille.
 Une autre relation de conjugaison
Une autre relation de conjugaison
Nous pouvons également obtenir une relation similaire, avec origine au centre de la lentille cette fois-ci. En partant de la formule du grandissement :
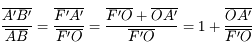
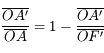
 Relation de conjugaison de Descartes (avec origine au centre)
Relation de conjugaison de Descartes (avec origine au centre)
On obtient ainsi la relation de conjugaison de Descartes :
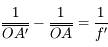
Auteur: B. Mollier
 Lunettes pour myope
Lunettes pour myope
Difficulté : ☆☆
Temps : 10 min
Considérons une paire de lunettes correctrices pour la myopie. L'ordonnance indique une vergence de 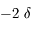 .
.

Crédit :
B. Mollier
Question 1)
Quelle est la distance focale image de la paire de lunettes ? Quelle est le type de lentilles utilisées ?
Question 2)
Muni de cette paire de lunettes, je lis un livre situé à 30 cm de mon visage. Quelle est la distance de l'image de cet ouvrage à travers les lunettes ?
Auteur: B. Mollier
 Condition de formation d'image
Condition de formation d'image
Difficulté : ☆☆☆
Temps : 20 min
On dispose d'un objet, d'un écran, et d'une lentille convergente de distance focale image 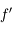 .
.
Question 1)
Quelle doit être la distance minimale 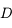 entre l'objet et l'écran pour pouvoir y former son image ?
entre l'objet et l'écran pour pouvoir y former son image ?

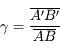

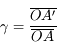



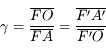

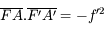
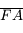 sur les figures,
sur les figures,
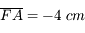
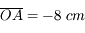
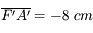
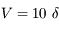 . On place un objet à une distance
. On place un objet à une distance 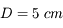 en amont du centre de la lentille.
en amont du centre de la lentille.
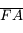 en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
en appliquant la relation de Chasles. En déduire la position de l'image en appliquant la formule de Newton.
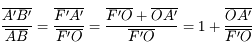
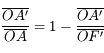
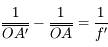
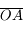 et
et 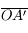 respectivement
respectivement 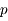 et
et 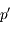 .
.
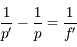
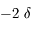 .
.

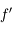 .
.
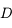 entre l'objet et l'écran pour pouvoir y former son image ?
entre l'objet et l'écran pour pouvoir y former son image ?
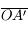 en fonction de
en fonction de 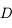 et
et 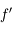 . Déduisez-en une condition sur
. Déduisez-en une condition sur 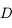 pour que l'image existe.
pour que l'image existe.
 , l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.
, l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre. , l'image est 3 fois plus petite et dans le même sens que l'objet.
, l'image est 3 fois plus petite et dans le même sens que l'objet. , l'image est 2 fois plus grande et dans le même sens que l'objet.
, l'image est 2 fois plus grande et dans le même sens que l'objet. , l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.
, l'image et l'objet font la même taille mais sont inversés l'un par rapport à l'autre.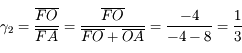 , l'image est 3 fois plus petite et dans le même sens que l'objet.
, l'image est 3 fois plus petite et dans le même sens que l'objet.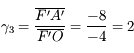 , l'image est 2 fois plus grande et dans le même sens que l'objet.
, l'image est 2 fois plus grande et dans le même sens que l'objet.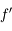 vaut
vaut 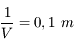 .
.
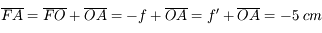 .
.
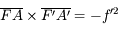
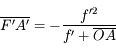
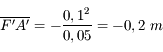
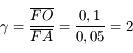
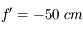 . Cette distance est négative, il s'agit donc de lentilles divergentes.
. Cette distance est négative, il s'agit donc de lentilles divergentes.
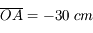 .
.
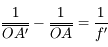 d'où
d'où 
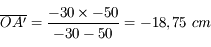
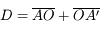 .
.
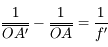
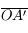 en fonction de
en fonction de 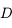 et
et 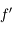
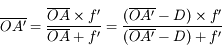
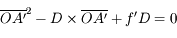
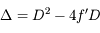
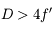 . Si la distance entre l'objet et l'écran est inférieure à 4 fois la distance focale, il sera impossible de faire apparaître l'image sur l'écran !
. Si la distance entre l'objet et l'écran est inférieure à 4 fois la distance focale, il sera impossible de faire apparaître l'image sur l'écran !