 Lentille convergente utilisée comme une loupe
Lentille convergente utilisée comme une loupe
Prenons une lentille convergente. Utilisons la d'abord comme une loupe. En observant un objet (un timbre, par exemple) dans la direction perpendiculaire à lui, on peut obtenir, en plaçant judicieusement la loupe, une image nette et agrandie du timbre. Nous nous trouvons donc dans des conditions de stigmatisme et d'aplanétisme au moins approché. Si on s'amuse à déplacer un écran derrière notre lentille pour obtenir une image de notre timbre, c'est peine perdue. Nous avons donc une image virtuelle, l'objet étant tout ce qu'il y a de plus réel.
 Lentille convergente utilisée comme un projecteur
Lentille convergente utilisée comme un projecteur
Remplaçons cette fois le timbre par un objet rétroéclairé (les opticiens aiment bien utiliser un F éclairé par l'arrière). Plaçons un écran suffisamment loin de lui. Si on déplace la lentille, on trouve deux positions où l'on obtient une image inversée du F, tantôt plus grande, tantôt plus petite. On a donc cette fois-ci une image réelle. Tiens, une lentille convergente peut produire les deux types d'images à partir d'un objet réel. Nous allons détailler cela dans la suite.
 Foyer principal image
Foyer principal image
Considérons un faisceau parallèle (objet à l'infini) et parallèle à l'axe optique (cas du Soleil à travers une loupe) et observons ce qui se passe. Dans le cas d'une lentille convergente, tous les rayons convergent en un point. Nous appellerons ce point foyer principal image. Ce point est l'image réelle d'un point situé à l'infini. Dans le cas d'une lentille divergente, tous les rayons divergent. Cependant, ils semblent tous provenir d'un point situé en amont de la lentille (il suffit de les prolonger). Nous appellerons également ce point foyer principal image. Il est l'image virtuelle d'un point situé à l'infini.
Qu'advient-il d'un faisceau parallèle au passage d'une lentille ?

Crédit :
B. Mollier
 Définition
Définition
Le foyer principal image est le point image d'un point objet situé à l'infini sur l'axe optique.
Foyer principal objet
Par retour inverse de la lumière, si on place une source ponctuelle au foyer image, les rayons ressortiront parallèles. La lentille étant symétrique, on peut la retourner. Il existe donc un point où si l'on place une source ponctuelle, les rayons issus de ce point seront parallèles entre eux et parallèles à l'axe optique. Ce point est appelé foyer principal objet. Il est le symétrique par rapport à la lentille de foyer principal image. Dans le cas d'une lentille convergente, ce point est le point objet réel donnant une image à l'infini. Dans le cas d'une lentille divergente, ce point est le point objet virtuel donnant une image à l'infini.
Foyer principal objet

Le foyer principal objet est l'antécédent d'un point image situé à l'infini sur l'axe optique.
Crédit :
B. Mollier
 Définition
Définition
Le foyer principal objet est l'antécédent d'un point image situé à l'infini sur l'axe optique.
 Distance focale image
Distance focale image
On appelle distance focale image la distance séparant le centre de la lentille au foyer image. On la note 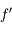 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière. 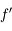 est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.
est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.
Distance focale image
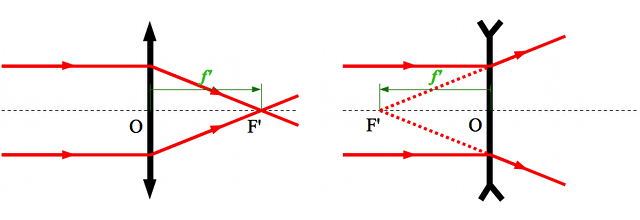
En vert, on définit la distance focale image
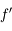
comme étant la distance du centre
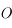
de la lentille au foyer principal image
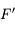
. Notez le sens de la flèche. Dans le cas d'une lentille convergente, elle est dans le même sens que celui de la propagation de la lumière. Cette distance est alors positive. Dans le cas de la lentille divergente, cette flèche est dans le sens opposé à la propagation de la lumière. Cette distance est alors comptée négativement. Pour plus d'information sur ces notions de distances positives et négatives, lisez cette
page.
Crédit :
ASM/B. Mollier
 Distance focale objet
Distance focale objet
De la même manière, on définit la distance focale objet comme étant la distance séparant le centre de la lentille et le foyer principal objet. Les deux foyers 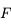 et
et 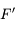 étant symétriques par rapport au centre
étant symétriques par rapport au centre 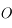 , on obtient
, on obtient 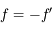 .
.
Distance focale objet
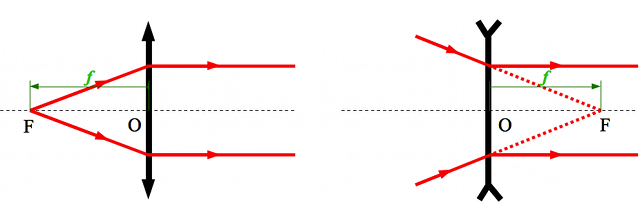
On définit la distance focale objet
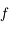
comme étant la distance séparant le centre de la lentille et le foyer principal objet. Là encore, le sens des flèches à son importance.
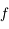
est négative dans le cas d'une lentille convergente et positive dans le cas d'une lentille divergente.
Crédit :
ASM/B. Mollier
Nous avons commencé à parler de distance négative et de grandeurs algébriques. Voici un petit aparté pour détailler ces notions.
 Excusez-moi m'dame, où est la boulangerie ?
Excusez-moi m'dame, où est la boulangerie ?
Dans la rue, quelqu'un vous demande où se situe la boulangerie la plus proche. Vous lui indiquez qu'elle est à 100 m. Oui, mais cette indication ne précise pas si elle est à 100 m devant ou derrière. Certes, en général, c'est implicite, ou accompagné d'un geste pour préciser la direction à emprunter. Cependant, en physique, il y a rarement quelqu'un pour nous indiquer le sens. Comment s'en sortir ? Si la boulangerie se situe devant nous, nous dirons effectivement qu'elle est à 100 m. Et si elle est derrière, qu'elle est à -100 m. C'est ce qu'on appelle des grandeurs algébriques. Il reste cependant encore un problème à régler. Si on se retourne, ce qui était devant devient derrière et inversement. Il faut en fait choisir un sens pour orienter nos mesures. Reprenons notre rue. Si elle est à sens unique, le plus simple est de choisir le sens de circulation des voitures pour orienter notre axe. Les distances dans le sens de circulation seront positives, et celle dans le sens opposé seront négatives.
Mesures algébriques
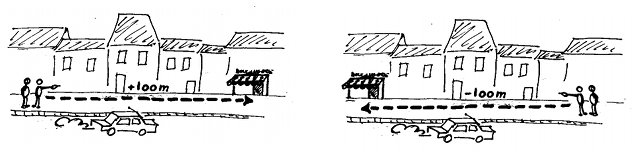
La boulangerie est située devant ? Elle est à + 100 m. Elle est située derrière ? Elle est à - 100 m.
Crédit :
B. Mollier
 Grandeurs algébriques en optique
Grandeurs algébriques en optique
En optique, ce sera pareil. Sauf que de circulation il n'est pas question. Mais nous prendrons pour orienter notre axe optique le sens de parcours des photons. Les distances orientées dans le même sens que l'axe optique seront comptées positivement (comme la distance focale image pour une lentille convergente), et celles dans le sens opposé seront comptées négativement (comme la distance focale objet pour une lentille convergente).
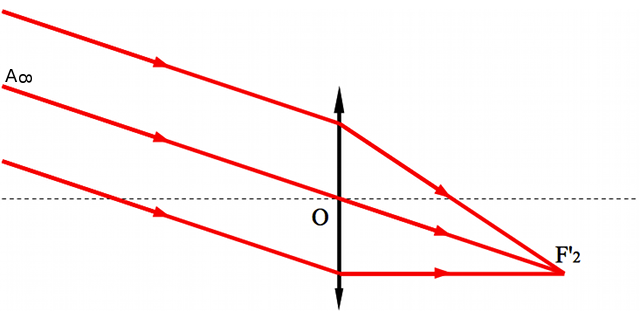
Considérons un faisceau parallèle mais arrivant avec une incidence non nulle par rapport à l'axe optique. Dans le cas de la lentille convergente, ils convergent en point appartenant nécessairement à l'axe 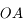 car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
Exemple de foyer secondaire dans le cas d'un lentille convergente
Crédit :
ASM/B. Mollier
Remarque : En fait, cette dernière remarque est vraie dans l'approximation de Gauss, qui garantit un aplanétisme approché.
Si l'inclinaison du faisceau varie, ce point (le foyer secondaire) parcourt ce que l'on nomme le plan focal de la lentille.
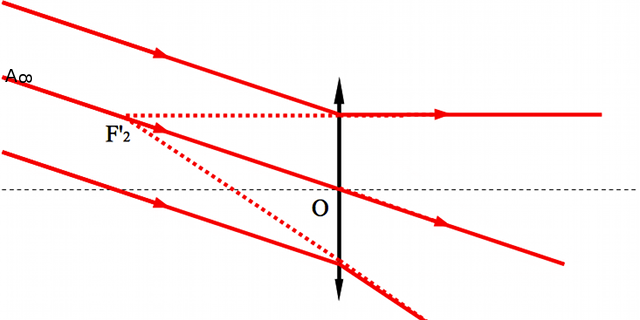
Pour une lentille divergente, on retrouve le même phénomène, sauf que les foyers secondaires images sont virtuels et situés en amont de la lentille. Comme précédemment, nous allons pouvoir définir un foyer secondaire objet, comme étant l'antécédent d'un point image situé à l'infini, en dehors de l'axe optique. L'ensemble des foyers secondaires objets constitueront le plan focal objet.
Exemple de foyer secondaire pour une lentille divergente
Crédit :
ASM/B. Mollier
Dans les conditions de Gauss, les plans focaux sont perpendiculaires à l'axe optique. Dans la vraie vie, ce sont des surfaces non planes. Les plaques photos utilisées au foyer d'un télescope de Schmidt étaient sphériques.
Munis de ces outils, nous allons pouvoir définir quelques propriétés sur les rayons lumineux traversant des lentilles. Elles vont nous permettre d'aborder, au paragraphe suivant, la construction des images.
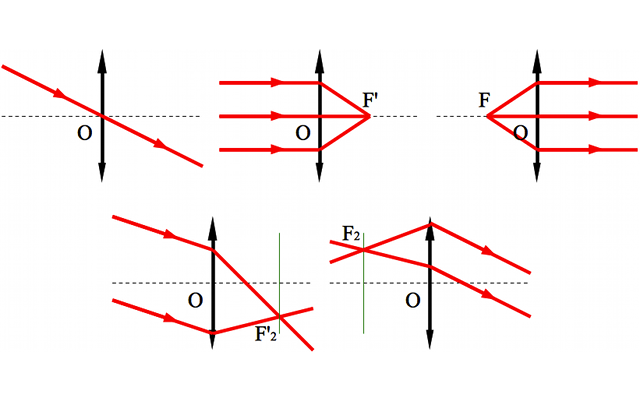
- Tout rayon passant par le centre de la lentille n'est pas dévié.
- Tout rayon parallèle à l'axe optique converge au foyer principal image.
- Tout rayon passant par le foyer principal objet ressort parallèle à l'axe optique.
- Deux rayons parallèles entre eux se croisent dans le plan focal image.
- Deux rayons se croisant dans le plan focal objet ressortent parallèles entre eux.
Résumé
Crédit :
ASM/B. Mollier
 Lentille convergente utilisée comme une loupe
Lentille convergente utilisée comme une loupe Lentille convergente utilisée comme un projecteur
Lentille convergente utilisée comme un projecteur
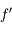 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière. 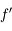 est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.
est positif dans le cas d'une lentille convergente et négatif dans le cas d'une divergente.

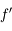 comme étant la distance du centre
comme étant la distance du centre 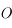 de la lentille au foyer principal image
de la lentille au foyer principal image 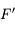 . Notez le sens de la flèche. Dans le cas d'une lentille convergente, elle est dans le même sens que celui de la propagation de la lumière. Cette distance est alors positive. Dans le cas de la lentille divergente, cette flèche est dans le sens opposé à la propagation de la lumière. Cette distance est alors comptée négativement. Pour plus d'information sur ces notions de distances positives et négatives, lisez cette
. Notez le sens de la flèche. Dans le cas d'une lentille convergente, elle est dans le même sens que celui de la propagation de la lumière. Cette distance est alors positive. Dans le cas de la lentille divergente, cette flèche est dans le sens opposé à la propagation de la lumière. Cette distance est alors comptée négativement. Pour plus d'information sur ces notions de distances positives et négatives, lisez cette 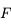 et
et 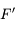 étant symétriques par rapport au centre
étant symétriques par rapport au centre 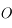 , on obtient
, on obtient 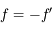 .
.

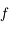 comme étant la distance séparant le centre de la lentille et le foyer principal objet. Là encore, le sens des flèches à son importance.
comme étant la distance séparant le centre de la lentille et le foyer principal objet. Là encore, le sens des flèches à son importance. 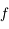 est négative dans le cas d'une lentille convergente et positive dans le cas d'une lentille divergente.
est négative dans le cas d'une lentille convergente et positive dans le cas d'une lentille divergente.
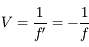
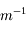 ou encore en dioptrie (noté
ou encore en dioptrie (noté 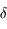 ). Par exemple, une lentille divergente de distance focale
). Par exemple, une lentille divergente de distance focale 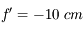 (correction pour une myopie sévère) possède une vergence de
(correction pour une myopie sévère) possède une vergence de 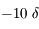 . C'est le nombre annoncé dans les ordonnances pour les lunettes.
. C'est le nombre annoncé dans les ordonnances pour les lunettes.

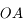 car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
car tout rayon passant par le centre de la lentille n'est pas dévié. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.


