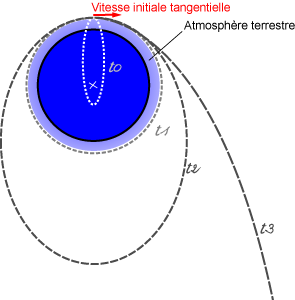
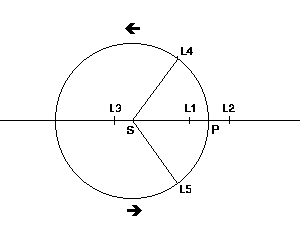
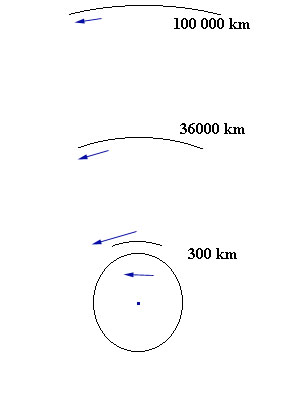
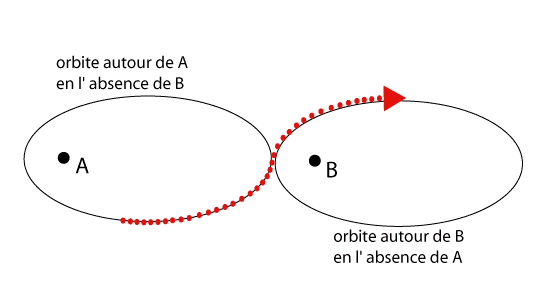
Dans le système solaire on trouve plus de deux corps et pour obtenir les mouvements des planètes avec une très bonne précision, il faut envisager un problème de N corps s'attirant mutuellement.
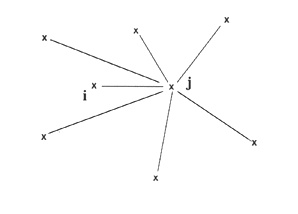
![F_j = \[\sum_{i=1 (i\neq j)}^N\]\frac{k~m_i~m_j~P_i~P_j}{\mid P_i~P_j\mid ^3}](../pages_mecanique-celeste/equations_dynamique-systeme/equation1.png)
Mais si on regarde d'un peu plus près, on se rend compte qu'on est en présence d'un très gros corps, le Soleil, mille fois plus massif que la plus grosse des planètes, Jupiter, entouré de petits corps tournant autour de lui. Chaque couple Soleil-planète est un problème à deux corps. On peut considérer en première approximation la masse m de la planète comme négligeable devant celle du Soleil (notée M) et la force subie par la planète est alors :
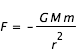
Le coefficient GM, produit de la constante gravitationnelle et de la masse du Soleil, est alors le même pour toutes les planètes, ce que Kepler (1571-1630) avait remarqué sans le démontrer.
Dans le cas de N corps, on considérera que l'on a toujours des mouvements de deux corps deux à deux avec une perturbation par les autres corps entraînant une variation des paramètres de l'orbite elliptique du petit corps tournant autour du plus gros. C'est Lagrange (1736-1813) qui introduisit les équations décrivant ces mouvements perturbés.