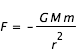La mécanique céleste
Auteur: Jean-Eudes Arlot
- Introduction
- Dynamique et gravitation
- Le principe fondamental de la dynamique
- En savoir plus: le principe fondamental de la mécanique
- Histoire : les débuts de la mécanique
- La gravitation universelle
- La mécanique céleste
- Dynamique du système solaire
- Le problème à deux corps
- Les mouvements dans le système solaire
- La vitesse de libération
- Les points de Lagrange
- Les satellites géostationnaires
- En savoir plus: calcul des périodes des satellites artificiels de la Terre
- Les transferts d'orbites par impulsion gravitationnelle
- Les satellites gardiens des anneaux
- QCM
- Les théories du mouvement des planètes
- Remarques générales sur les théories planétaires
- En savoir plus: théories analytiques ou intégration numérique ?
- En savoir plus: La découverte de Neptune par Le Verrier
- L'argument temps dans les théories planétaires
- Application : l'évolution de l'excentricité de l'orbite terrestre
- QCM
Introduction
 Introduction
Introduction
Les lois de Kepler ne sont qu'une description empirique cinématique de ce que l'on observe. En fait, le mouvement des astres est régi par des principes plus fondamentaux qui vont permettre d'expliquer de nombreux phénomènes: ce sont les principes de la mécanique céleste.
Dynamique et gravitation
Le principe fondamental de la dynamique
Le principe fondamental de la dynamique est un outil développé dans le cadre de la mécanique classique, qui permet de faire le lien entre les forces appliquées à un corps et l'évolution cinématique de ce corps. Appliqué à un solide de masse m dont le mouvement est défini dans un référentiel dit galiléen, le principe s'énonce :
F = m γ = m dv / dt
F représente l'ensemble des forces appliquées à l'objet, et γ son accélération. dv / dt est la dérivée de la vitesse par rapport au temps (soit l'accélération).
En savoir plus: le principe fondamental de la mécanique
 En savoir plus
En savoir plus
Appliquée à un point matériel (un solide de dimension négligeable devant les distances mises en jeu) ou à un ensemble de points matériels, cette loi peut se réécrire de diverses manières, toutes équivalentes :
- le théorème du mouvement du centre de masse (ou barycentre) :
"le barycentre d'un système matériel se meut comme si toute la masse du système y était transportée, les forces extérieures au système agissant toutes sur ce barycentre"
- le théorème du moment cinétique appliqué à un point matériel :
"la dérivée par rapport au temps du moment cinétique en un point d'un système matériel est, à chaque instant, égale au moment résultant des forces extérieures par rapport à ce même point"
- le théorème de l'énergie cinétique (autrefois appelé théorème des forces vives) :
"la variation de l'énergie cinétique d'un système matériel pendant un intervalle de temps donné est égal à la somme des travaux des forces intérieures et extérieures appliquées à ce système pendant cet intervalle de temps".
Notons que du théorème du moment cinétique découle directement la deuxième loi de Kepler (lois des aires), résultant du seul fait que l'interaction gravitationnelle est une force "centrale".
Histoire : les débuts de la mécanique
On doit ces principes à Galilée et Huygens, mais ils ont été affinés par la suite par Clairaut, Descartes, Euler et D'Alembert.
Galilée (1564-1642) était d'abord un physicien et il étudia la mécanique et la dynamique des corps en mouvement. Il démontra l'invariance de l'accélération dans le champ de pesanteur terrestre à la surface du globe et établit la loi de l'inertie (tout corps non soumis à une force extérieure est animé d'un mouvement rectiligne uniforme et se trouve dans un référentiel que l'on nomme aujourd'hui "galiléen").
Christian Huygens (1629-1695), hollandais, développa une théorie ondulatoire de la lumière. En 1673, il publia la loi sur l'accélération centrifuge des corps en mouvement circulaire. Il séjourna quinze ans en France sur l'invitation de Colbert.
René Descartes (1596-1650) apporta alors une vision complètement nouvelle de l'univers. L'univers évolue seul : il n'est point besoin d'un dieu intervenant à tout moment. Descartes étudia l'optique et fit une théorie de la réflexion et de la réfraction. Il introduisit les concepts mathématiques en physique, en particulier un système de coordonnées aujourd'hui dites cartésiennes facilitant les calculs.
Alexis Clairaut (1713-1765) fut l'un des membres de l'expédition en Laponie. Il s'attaqua à des problèmes de mécanique céleste comme celui des 3 corps appliqué au système Terre-Lune perturbé par le Soleil. Il appliqua la théorie de la gravitation universelle aux comètes, en particulier aux perturbations de Jupiter et Saturne sur la trajectoire de la comète de Halley.
Leonhard Euler (1707-1783), mathématicien suisse, étudia les perturbations mutuelles de Jupiter et de Saturne ainsi que les orbites paraboliques des comètes. On lui doit la définition des "angles d'Euler" permettant la détermination de la position d'un solide en mouvement dans un trièdre trirectangle.
Jean-Baptiste Le Rond d'Alembert (1717-1783) publia un traité de dynamique contenant le théorème sur les forces d'inertie connu aujourd'hui sous le nom de théorème de d'Alembert. Il établit également les équations du mouvement de la Terre autour de son axe et réalisa la première théorie mathématique de la précession.
La gravitation universelle
Le caractère universel de la gravitation a été mis en évidence par Newton (1642-1727) dans son œuvre "Principes mathématiques de philosophie naturelle". Newton a été le premier à comprendre que la pomme qui tombe d'un arbre et la Lune qui tourne autour de la Terre obéissent à une même loi et que leurs mouvements sont en fait de même nature.
La loi de la gravitation universelle s'énonce ainsi : "deux points matériels de masse m et m' exercent l'un sur l'autre une force attractive directement proportionnelle aux masses et inversement proportionnelle au carré de la distance r les séparant". Le module F de cette force vaut :
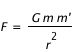 où G est la constante gravitationnelle.
où G est la constante gravitationnelle.
Cette loi suppose la transmission instantanée des forces dans l'espace.

Portrait de Sir Isaac Newton
Crédit :
Danielle Briot - Collection particulière
La mécanique céleste
La mécanique céleste est alors l'application de la mécanique newtonienne et des principes fondamentaux de la mécanique aux corps du système solaire. C'est Laplace qui a mis en place les fondements de la mécanique céleste qui va (presque) tout expliquer :
- le mouvement des planètes et de leurs satellites
- la précession et la nutation
- les marées
- l'applatissement des planètes
En première approximation, la mécanique newtonienne explique donc parfaitement les mouvements dans le système solaire. Mais avant d'aborder un cas aussi complexe, on s'intéresse d'abord au problème restreint à 2 corps.

Pierre Simon de Laplace
Crédit :
Danielle Briot - Collection particulière
Dynamique du système solaire
Le problème à deux corps
Le problème à 2 corps s'intéresse à 2 solides, assimilés à leur centre de masse, seuls à interagir. Ce problème est soluble analytiquement, relativement simplement, en travaillant dans le référentiel du centre de masse du système ; le reste de l'Univers étant oublié, le centre de masse est isolé et fournit un bon référentiel galiléen pour l'étude du mouvement.
- Tout d'abord, on peut montrer que le mouvement des 2 corps l'un autour de l'autre est plan. Ceci résulte du fait que le moment cinétique du système est constant, car l'interaction est centrale, toujours dirigée vers le barycentre du système.
- Ensuite, l'interaction gravitationnelle se traduisant par un "champ de force", il en découle que l'énergie du système est également constante.
- Enfin, le module de la force évoluant comme l'inverse du carré de la distance entre les 2 corps, un autre invariant apparaît. Cet invariant se traduit par le vecteur excentricité, et la trajectoire relative d'un corps par rapport à l'autre s'apparente à un cercle, une ellipse, une parabole ou une hyperbole. Cette trajectoire, dans le plan du mouvement, est définie par son demi-grand axe, de mesure a, et l'excentricité e.
C'est dans le cadre de plusieurs problèmes à deux corps (pour chaque couple planète-Soleil) que s'appliquent les lois de Kepler.
Les mouvements dans le système solaire
Dans le système solaire on trouve plus de deux corps et pour obtenir les mouvements des planètes avec une très bonne précision, il faut envisager un problème de N corps s'attirant mutuellement.
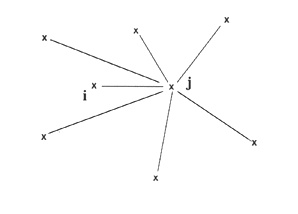
Le principe du problème des N corps de masse m
i
Chacun des N corps de masse m
i exerce sur le corps repéré par j une force proportionnelle au produit de leurs masses, et inversement proportionnelle au carré de leur distance. Cette force s'écrit :
![F_j = \[\sum_{i=1 (i\neq j)}^N\]\frac{k~m_i~m_j~P_i~P_j}{\mid P_i~P_j\mid ^3}](../pages_mecanique-celeste/equations_dynamique-systeme/equation1.png)
Crédit : CNRS/Jean-Eudes Arlot
Mais si on regarde d'un peu plus près, on se rend compte qu'on est en présence d'un très gros corps, le Soleil, mille fois plus massif que la plus grosse des planètes, Jupiter, entouré de petits corps tournant autour de lui. Chaque couple Soleil-planète est un problème à deux corps. On peut considérer en première approximation la masse m de la planète comme négligeable devant celle du Soleil (notée M) et la force subie par la planète est alors :
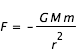
Le coefficient GM, produit de la constante gravitationnelle et de la masse du Soleil, est alors le même pour toutes les planètes, ce que Kepler (1571-1630) avait remarqué sans le démontrer.
Dans le cas de N corps, on considérera que l'on a toujours des mouvements de deux corps deux à deux avec une perturbation par les autres corps entraînant une variation des paramètres de l'orbite elliptique du petit corps tournant autour du plus gros. C'est Lagrange (1736-1813) qui introduisit les équations décrivant ces mouvements perturbés.
La vitesse de libération
Lorsque l'on veut quitter un corps céleste -la Terre par exemple- et échapper à son attraction, il faut vaincre les forces de gravitation et surtout éviter de retomber sur le sol. Deux cas se présentent :
- éviter de retomber sur le sol mais rester en orbite autour de la Terre : trajectoire fermée (cercle ou ellipse)
- quitter l'attraction terrestre en s'éloignant indéfiniment (trajectoire hyperbolique)
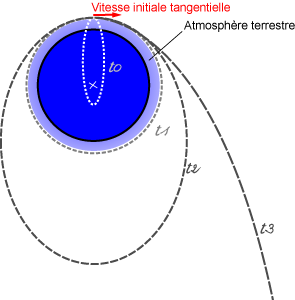
Crédit : CNRS / Jean-Eudes Arlot et ASM / Gilles Bessou
En première approximation, la trajectoire d'une pierre lancée depuis le sol est une parabole si on suppose la Terre plate et le centre d'attraction à l'infini. En réalité, la trajectoire est une ellipse dont le centre de la Terre est le foyer. Il faut circulariser l'orbite pour éviter que la trajectoire heurte la surface terrestre. Notons que l'altitude minimum pour satelliser un objet est de 300 km pour éviter le freinage par l'atmosphère terrestre.
- v > 8 km/s : la trajectoire est circulaire et ne heurte plus la Terre (trajectoire T1)
- v < 8 km/s : la vitesse est insuffisante et l'objet retombe sur Terre (trajectoire T0)
- 8 km/s < v < 13 km/s : la trajectoire est une ellipse dont le périgée correspond au point de lancement (trajectoire T2 fermée)
- v > 13 km/s : la trajectoire n'est plus fermée ; le mobile va s'éloigner à l'infini sur une trajectoire hyperbolique
Les points de Lagrange
Sur l'orbite décrite par un corps autour d'une masse centrale, on va trouver des points d'équilibre utiles pour les satellites artificiels d'observation : les points de Lagrange.
Pour obtenir une modélisation des mouvements dans le système solaire, on va partir du problème simplifié dans lequel les trajectoires des planètes sont des ellipses mais les éléments de ces ellipses vont varier au cours du temps. Cette ellipse de base est appelée ellipse osculatrice. Pour chaque planète on va considérer un problème à deux corps perturbé par les autres planètes. C'est Lagrange (1736-1813) au XVIIIème siècle qui a posé les équations du problème. Lagrange a aussi noté que dans un système à deux corps, il existait des positions d'équilibre où des corps supplémentaires pouvaient rester captifs. Ces positions sont appelées aujourd'hui les points de Lagrange du système à deux corps. La figure ci-dessous montrent l'emplacement des 5 points L1, L2, L3, L4, L5. Seuls les points L4 et L5 sont des points d'équilibre stables. Des astéroïdes sont piégés sur ces points de l'orbite de Jupiter et de celle de Mars. Les points L1 et L2 de la Terre permettent d'installer des télescopes d'observation (SOHO, un satellite d'observation du Soleil en L1 et bientôt GAIA, un satellite d'observation astrométrique de la galaxie en projet en L2). Les points L1 et L2 sont à 1,5 millions de kilomètres de la Terre.
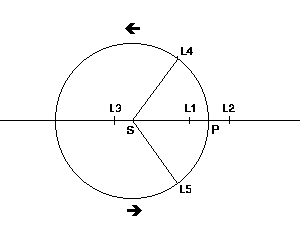
Les points de Lagrange L1, L2, L3, L4 et L5 par rapport à l'orbite
d'une planète P autour du Soleil S. Seuls L4 et L5 sont stables.
Les angles (SP, SL4) et (SP, SL5) font chacun 60°.
Crédit : CNRS / Jean-Eudes Arlot
Les satellites géostationnaires
Un satellite géostationnaire est vu immobile depuis la surface de la Terre : pourquoi ? Non pas parce qu'il est réellement immobile par rapport à la Terre, mais parce qu'il tourne à la même vitesse que la Terre autour de son axe. Il doit faire une révolution en 24 heures ! (en fait en 23 heures 56 minutes 4 secondes qui est la période de rotation sidérale autour de la Terre).
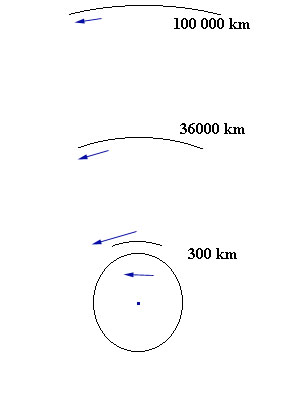
Période de révolution selon l'altitude
Altitude 100 000 km : 3,5 jours
Altitude 36 000 km : 24 heures
Altitude 300 km : 1 heure et demie
Crédit : CNRS / Jean-Eudes Arlot
En savoir plus: calcul des périodes des satellites artificiels de la Terre
 En savoir plus
En savoir plus
Un satellite artificiel de la Terre tourne d'autant moins vite qu'il est loin de la Terre pour respecter la 3ème loi de Kepler qui dit que a3/T2 est une constante pour les objets tournant autour d'un même corps, où a est le demi-grand axe de l'orbite et T la période de révolution.
Cette constante est, pour la Terre : GM/4π2 où G est la constante de la gravitation et M la masse de la Terre soit :
G=6,67259x10-11 m3kg-1s-2 et M=5,9736x1024 kg et donc GM/4π2 = 1,00965x1013
En supposant les orbites circulaires, un satellite situé à 300 km d'altitude (orbite basse) aura une période de révolution de T :
a = 300 km + 6378 km = 6,678x106 m ; donc a3 = 297,81x1018 m3
Appliquons la formule a3/T2 = GM/4π2 = 1,00965.1013
donc T2 = a3/1,00965x1013 = 297,81x1018/1,00965x1013 = 29496358 secondes, soit T = 5431,055 secondes, c'est-à-dire, environ une heure et demie.
Calculons la distance a au centre de la Terre à laquelle doit se trouver un satellite artificiel pour être géostationnaire.
T doit être égal à 23 heures 56 minutes 4 secondes, soit 86164 secondes ; on a T2 = 7424234896 s2 donc a3 = T2x1,00965x1013 = 74,95878763x1021 (voir ci-dessus) et ainsi a = 4,21639 x 107 mètres soit 42 163 km. En retranchant le rayon terrestre, on obtient l'altitude d'un satellite géostationnaire : environ 36 000 kilomètres.
On peut faire le même calcul avec des satellites plus éloignés et on verra que la durée de révolution augmente et atteint 28 jours pour un corps situé à 300 000 kilomètres de la Terre : c'est la Lune !
Les transferts d'orbites par impulsion gravitationnelle
Les sondes spatiales utilisent le "rebond" gravitationnel pour aller plus loin et plus vite, en économisant du carburant, nécessaire pour échapper à l'attraction terrestre. On utilise pour cela les lois de Kepler et le mouvement des deux corps : la sonde va suivre un mouvement képlérien par rapport à un corps central A, la Terre, par exemple. Le corps A est prépondérant et on va mettre la sonde sur une orbite elliptique dont l'apogée est proche d'un autre corps que l'on va utiliser. A l'apogée (point de l'orbite le plus éloigné du corps A), la présence prépondérante du corps B va modifier la trajectoire de la sonde. Des petites manoeuvres vont permettre de mettre la sonde sur une nouvelle orbite elliptique centrée sur le corps B pour lui permettre d'avoir une nouvelle trajectoire.
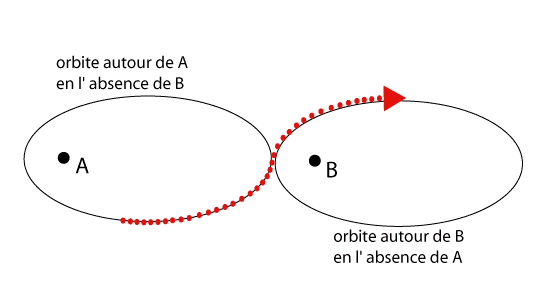
Ce principe est couramment utilisé par les sondes qui doivent se diriger vers l'extérieur du système solaire (planètes Jupiter, Saturne, Uranus et Neptune).
Crédit : CNRS / Jean-Eudes Arlot
Les satellites gardiens des anneaux

Crédit : NASA/C. J. HAMILTON
Les planètes géantes présentent la particularité d'être entourées d'anneaux. Saturne possède le plus spectaculaire. La formation d'un anneau est le résultat des collisions entre une mutlitude de petits cailloux en orbite autour de la planète. Ces petites particules de roche et de glace étant en rotation autour de la planète, elles s'organisent sous forme d'un disque plat.
Les divisions - espaces vides - qui apparaissent à l'intérieur d'un même anneau, sont longtemps restées inexpliquées. C'est la découverte de petits satellites orbitant dans ces espaces vides qui nous ont fournis l'explication.
Ci-contre, on a représenté un satellite orbitant dans une des divisions d'un anneau.
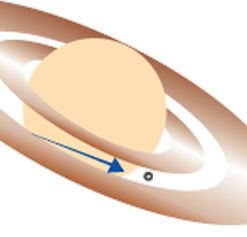
Premier temps : une particule se détache de l'anneau et pénètre dans la division ; elle s'approche du satellite.
Crédit : ASM

Deuxième temps : le satellite va modifier la trajectoire de la particule (mouvement des deux corps) et augmenter l'excentricité de sa trajectoire. Elle retournera donc dans l'anneau.
Crédit : ASM
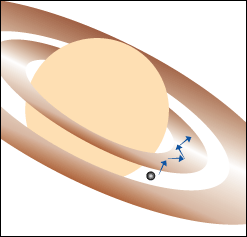
Troisième temps : de retour dans l'anneau, la particule subira de nouveau des collisions qui vont circulariser son orbite et lui éviter de retourner dans la division.
Crédit : ASM
Ainsi, on a l'impression que le satellite repousse les cailloux hors de la division. Il n'y a pas d'effet de répulsion : tout est conforme aux lois de la gravitation universelle.
QCM
Les théories du mouvement des planètes
Remarques générales sur les théories planétaires
Le mouvement des planètes autour du Soleil est un cas particulier du problème des N corps pour lequel on n'a pas de solution exacte pour N supérieur à 2. Tous les corps s'attirent les uns les autres conformément à la loi de la gravitation mais on considère que les planètes ont une masse faible devant celle du corps central, le Soleil. On recherche des solutions approchées du problème fondées sur la théorie des perturbations, où les coordonnées sont des fonctions du temps t, des masses des corps en présence et des constantes d'intégration. On obtient ces solutions en construisant des théories analytiques ou en effectuant des intégrations numériques.
En savoir plus: théories analytiques ou intégration numérique ?
 En savoir plus
En savoir plus
Dans les théories analytiques, les coordonnées sont obtenues sous forme de combinaisons de fonctions algébriques et trigonométriques analytiques du temps t et des paramètres du problème, masses et constantes d'intégration. Calculer une position avec de telles théories est long mais relativement simple puisqu'il suffit de substituer le paramètre "temps" dans les séries. Jusqu'à l'apparition des ordinateurs, il était nécessaire de construire des tables intermédiaires à partir desquelles on pouvait fabriquer des éphémérides.
Les intégrations numériques donnent les valeurs numériques des coordonnées et des vitesses pour des valeurs t0, t0+h, t0+2h, etc., t0 étant le temps initial et h étant le pas d'intégration. Les méthodes d'intégration numérique sont bien adaptées aux calculs par ordinateur et elles ont été particulièrement utilisées aux Etats-Unis. Cependant, pour calculer une position, il est indispensable de construire des tables intermédiaires à l'aide de l'intégration numérique. Ces tables seront utilisées pour la fabrication des éphémérides.
En savoir plus: La découverte de Neptune par Le Verrier
 En savoir plus
En savoir plus
La mécanique céleste allait prouver sa force en permettant de découvrir une nouvelle planète dans le système solaire, par le calcul et non pas seulement par l'observation du ciel.
Le Verrier avait établi un modèle de mouvement d'Uranus à partir des lois de la dynamique et de la gravitation universelle. Mais la comparaison aux observations ne donnait pas satisfaction : Uranus se trouvait trop loin, par rapport à son orbite calculée. La différence ne pouvait pas être expliquée par l'imprécision des observations: elle était bien plus grande. Le Verrier supposa qu'un corps massif attirait Uranus hors de son orbite. Mais où pouvait bien se trouver ce corps ? Quel était-il ? L'étude des observations d'Uranus réalisées entre 1800 et 1850 permit d'en calculer la masse et la distance. L'orbite ainsi calculée montrait qu'il s'agissait d'une nouvelle planète, au-delà d'Uranus. Le même calcul fut fait par Adams en Angleterre mais c'est Le Verrier qui fit observer par Galle à Berlin en 1846 la nouvelle planète. En fait, l'orbite de Neptune était un peu différente de celle calculée, mais les observations d'Uranus disponibles ne permettaient pas une meilleure précision.
La découverte de Pluton au XXème siècle ne s'est pas faite ainsi, la masse de Pluton étant trop faible pour perturber neptune.
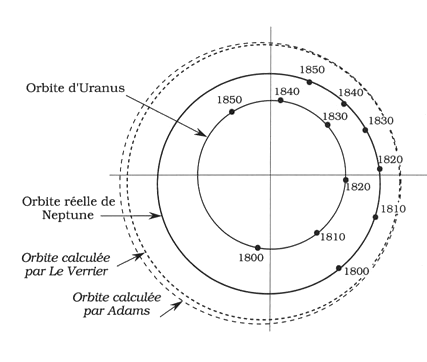
Orbite théorique et orbite observée avant la découverte de Neptune
Crédit : CNRS
L'argument temps dans les théories planétaires
Il convient de dire maintenant quelques mots sur l'argument "temps" des éphémérides. En effet, pour connaître une position à un instant donné, quel instant chercher dans les éphémérides ? Jusqu'en 1834, on a utilisé le temps solaire vrai de Paris. Ensuite, du fait de l'existence d'horloges plus fiables, on a utilisé le temps moyen de Paris. En 1916, suite à une convention internationale, on a utilisé le temps moyen de Greenwich. Ces temps étaient jusque là liés à la rotation de la Terre considérée comme suffisamment uniforme. La mise en évidence d'irrégularités dans cette rotation (ralentissement) amena les astronomes à introduire une échelle de temps uniforme pour le calcul des éphémérides, échelle de temps basée sur la révolution de la Terre autour du Soleil. On utilisa le Temps des éphémérides défini à partir de la théorie du Soleil de Newcomb, ou encore, comme dans la Connaissance des temps, le Temps uniforme de Le Verrier tiré de sa théorie du Soleil et donc très proche du précédent. A partir de 1984 on introduisit le Temps terrestre, temps uniforme construit à partir des horloges atomiques beaucoup plus stables que les mouvements célestes pour construire une échelle de temps.
Ainsi, si on utilise le Temps Universel comme argument des éphémérides, on verra les planètes accélérer... C'est en fait la Terre qui ralentit...
Application : l'évolution de l'excentricité de l'orbite terrestre
La mécanique céleste permet également d'obtenir, à une précision plus faible que celle des éphémérides valables sur quelques siècles, l'évolution des orbites planétaires sur de très longues durées de l'ordre de plusieurs millions d'années. On constate ainsi que l'excentricité de l'orbite terrestre subit de larges variations formées de nombreux termes périodiques dont les plus importants ont des périodes voisines de 100 000 ans, et pour l'un d'eux, une période de 400 000 ans. Les travaux de l'Institut de mécanique céleste, depuis les années 1970, ont permis de confirmer définitivement l'hypothèse astronomique des variations climatiques de la Terre au cours de l'ère quaternaire. Les paléoclimatologues montrent en effet la corrélation entre les variations des éléments de l'orbite terrestre et les grandes glaciations du quaternaire. L'orbite circulaire de la Terre correspond à une glaciation et une orbite elliptique à une période chaude. La grande précision de la mécanique céleste offre ainsi une horloge à la paléoclimatologie en lui donnant les dates des glaciations et des périodes interglaciaires.
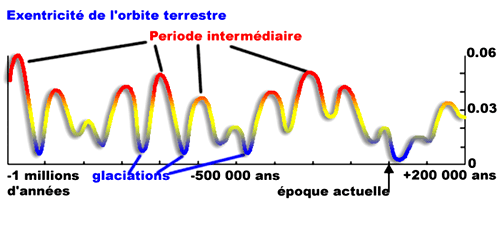
Variations de l'excentricité de l'orbite terrestre sur 1 200 000 ans.
Dans 27 000 ans l'excentricité sera presque nulle, l'orbite de la Terre presque circulaire ce qui entraînera une glaciation si, d'ici là, l'atmosphère de la Terre
n'est pas profondément modifiée.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
QCM
Réponses aux QCM
pages_dynamique-systeme/mctc-qcm-trajectoire.html
QCM
- Question 1
Solution : réponse 1)
(
L'ellipse est la solution du problème à deux corps, Terre+masse, mais en première approximation, c'est une parabole.
)
Solution : réponse 3)
(
L'ellipse est la solution du problème à deux corps Terre+masse, mais en première approximation, c'est une parabole.
)
- Question 2
Solution : réponse 3)
(
oui, il y a plus de deux corps dans le système solaire et les trajectoires sont très complexes bien que proches d'ellipses en déformation constante
)
- Question 3
Solution : réponse 3)
(
oui, à cette altitude la vitesse d'un satellite est la même que celle de la Terre autour de son axe et le satellite surplombe toujours la même région terrestre
)
pages_mouvements-planetes/mctc-qcm-planete.html
QCM
- Question 1
Solution : réponse 1)
(
oui, les perturbations sur Uranus étaient maximales à cette date, il y avait donc une planète supplémentaire pas bien loin
)
- Question 2
Solution : réponse 1)
(
(oui, c'est tout à fait par hasard que Tombaugh a découvert Pluton
)
- Question 3
Solution : réponse 1)
(
L'inclinaison de l'axe de la Terre et l'excentricité de l'orbite de la Terre ont une influence sur le climat. Dans le passé, une excentricité nulle a causé un age glaciaire.
)
Solution : réponse 3)
(
L'inclinaison de l'axe de la Terre et l'excentricité de l'orbite de la Terre ont une influence sur le climat de la Terre.
)
 Introduction
Introduction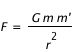 où G est la constante gravitationnelle.
où G est la constante gravitationnelle.



![F_j = \[\sum_{i=1 (i\neq j)}^N\]\frac{k~m_i~m_j~P_i~P_j}{\mid P_i~P_j\mid ^3}](../pages_mecanique-celeste/equations_dynamique-systeme/equation1.png)