Le mouvement des planètes autour du Soleil est un cas particulier du problème des N corps pour lequel on n'a pas de solution exacte pour N supérieur à 2. Tous les corps s'attirent les uns les autres conformément à la loi de la gravitation mais on considère que les planètes ont une masse faible devant celle du corps central, le Soleil. On recherche des solutions approchées du problème fondées sur la théorie des perturbations, où les coordonnées sont des fonctions du temps t, des masses des corps en présence et des constantes d'intégration. On obtient ces solutions en construisant des théories analytiques ou en effectuant des intégrations numériques.
 En savoir plus
En savoir plus
Dans les théories analytiques, les coordonnées sont obtenues sous forme de combinaisons de fonctions algébriques et trigonométriques analytiques du temps t et des paramètres du problème, masses et constantes d'intégration. Calculer une position avec de telles théories est long mais relativement simple puisqu'il suffit de substituer le paramètre "temps" dans les séries. Jusqu'à l'apparition des ordinateurs, il était nécessaire de construire des tables intermédiaires à partir desquelles on pouvait fabriquer des éphémérides.
Les intégrations numériques donnent les valeurs numériques des coordonnées et des vitesses pour des valeurs t0, t0+h, t0+2h, etc., t0 étant le temps initial et h étant le pas d'intégration. Les méthodes d'intégration numérique sont bien adaptées aux calculs par ordinateur et elles ont été particulièrement utilisées aux Etats-Unis. Cependant, pour calculer une position, il est indispensable de construire des tables intermédiaires à l'aide de l'intégration numérique. Ces tables seront utilisées pour la fabrication des éphémérides.
 En savoir plus
En savoir plus
La mécanique céleste allait prouver sa force en permettant de découvrir une nouvelle planète dans le système solaire, par le calcul et non pas seulement par l'observation du ciel.
Le Verrier avait établi un modèle de mouvement d'Uranus à partir des lois de la dynamique et de la gravitation universelle. Mais la comparaison aux observations ne donnait pas satisfaction : Uranus se trouvait trop loin, par rapport à son orbite calculée. La différence ne pouvait pas être expliquée par l'imprécision des observations: elle était bien plus grande. Le Verrier supposa qu'un corps massif attirait Uranus hors de son orbite. Mais où pouvait bien se trouver ce corps ? Quel était-il ? L'étude des observations d'Uranus réalisées entre 1800 et 1850 permit d'en calculer la masse et la distance. L'orbite ainsi calculée montrait qu'il s'agissait d'une nouvelle planète, au-delà d'Uranus. Le même calcul fut fait par Adams en Angleterre mais c'est Le Verrier qui fit observer par Galle à Berlin en 1846 la nouvelle planète. En fait, l'orbite de Neptune était un peu différente de celle calculée, mais les observations d'Uranus disponibles ne permettaient pas une meilleure précision.
La découverte de Pluton au XXème siècle ne s'est pas faite ainsi, la masse de Pluton étant trop faible pour perturber neptune.
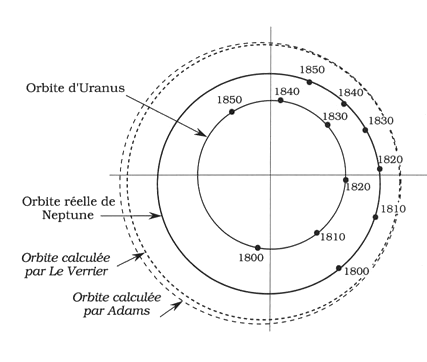
Orbite théorique et orbite observée avant la découverte de Neptune
Crédit : CNRS
Il convient de dire maintenant quelques mots sur l'argument "temps" des éphémérides. En effet, pour connaître une position à un instant donné, quel instant chercher dans les éphémérides ? Jusqu'en 1834, on a utilisé le temps solaire vrai de Paris. Ensuite, du fait de l'existence d'horloges plus fiables, on a utilisé le temps moyen de Paris. En 1916, suite à une convention internationale, on a utilisé le temps moyen de Greenwich. Ces temps étaient jusque là liés à la rotation de la Terre considérée comme suffisamment uniforme. La mise en évidence d'irrégularités dans cette rotation (ralentissement) amena les astronomes à introduire une échelle de temps uniforme pour le calcul des éphémérides, échelle de temps basée sur la révolution de la Terre autour du Soleil. On utilisa le Temps des éphémérides défini à partir de la théorie du Soleil de Newcomb, ou encore, comme dans la Connaissance des temps, le Temps uniforme de Le Verrier tiré de sa théorie du Soleil et donc très proche du précédent. A partir de 1984 on introduisit le Temps terrestre, temps uniforme construit à partir des horloges atomiques beaucoup plus stables que les mouvements célestes pour construire une échelle de temps.
Ainsi, si on utilise le Temps Universel comme argument des éphémérides, on verra les planètes accélérer... C'est en fait la Terre qui ralentit...
La mécanique céleste permet également d'obtenir, à une précision plus faible que celle des éphémérides valables sur quelques siècles, l'évolution des orbites planétaires sur de très longues durées de l'ordre de plusieurs millions d'années. On constate ainsi que l'excentricité de l'orbite terrestre subit de larges variations formées de nombreux termes périodiques dont les plus importants ont des périodes voisines de 100 000 ans, et pour l'un d'eux, une période de 400 000 ans. Les travaux de l'Institut de mécanique céleste, depuis les années 1970, ont permis de confirmer définitivement l'hypothèse astronomique des variations climatiques de la Terre au cours de l'ère quaternaire. Les paléoclimatologues montrent en effet la corrélation entre les variations des éléments de l'orbite terrestre et les grandes glaciations du quaternaire. L'orbite circulaire de la Terre correspond à une glaciation et une orbite elliptique à une période chaude. La grande précision de la mécanique céleste offre ainsi une horloge à la paléoclimatologie en lui donnant les dates des glaciations et des périodes interglaciaires.
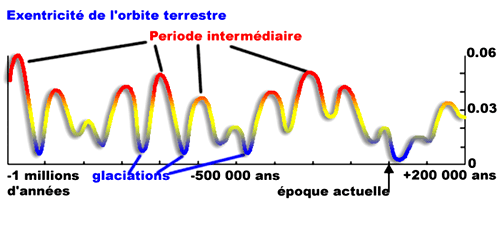
Variations de l'excentricité de l'orbite terrestre sur 1 200 000 ans.
Dans 27 000 ans l'excentricité sera presque nulle, l'orbite de la Terre presque circulaire ce qui entraînera une glaciation si, d'ici là, l'atmosphère de la Terre
n'est pas profondément modifiée.
Crédit : ASM/Jean-Eudes Arlot et Gilles Bessou
 En savoir plus
En savoir plus
