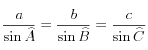La mesure des distances
Auteur: Jean-Eudes Arlot
- Introduction
- Comment mesurer une distance en astronomie ?
- La triangulation
- La parallaxe en astronomie
- Exercice
- La mesure par la parallaxe
- En savoir plus: la parallaxe horizontale
- Mesure de la distance Terre-Soleil et Terre-Planètes
- La nécessité d'un modèle théorique en astronomie
- Exercice
- La mesure de la Terre
- Passage d'un angle apparent à une distance
- Exercice
- La distance Terre-Lune
- La mesure de la distance Terre-Lune par les éclipses
Introduction
 Introduction
Introduction
Nous avons vu que l'astronome observe essentiellement des angles sur un ciel que l'on appelle la sphère céleste. Pourtant, tous les astres ne sont pas à la même distance de l'observateur. La Terre paraît plate et immobile. Comment, à partir de simples mesures d'angles, va-t-on pouvoir mesurer la taille de la Terre, la distance qui la sépare des astres du ciel et son mouvement dans l'espace?
Pour cela, deux notions vont être nécessaires.
La première est la notion de parallaxe : si deux observateurs voient un même objet sous deux angles différents, c'est que l'objet n'est pas à l'infini. La différence de vue ne dépend que de la position des observateurs et de la distance de l'objet observé. C'est le phénomène de relief, créé par notre cerveau à partir des images différentes reçues par nos deux yeux. Plus la distance de l'objet est grande, plus la distance entre les deux observateurs (entre les deux "yeux" qui observent) doit être grande.
La deuxième notion est celle d'un modèle théorique d'univers. On va supposer a priori des ordres de grandeur des quantités à mesurer et vérifier par l'observation et des mouvements des corps célestes. La vérification par l'observation ne sera pas une preuve que notre modèle est bon, mais qu'il colle momentanément avec l'observation. L'amélioration des mesures entraînera un écart entre l'observation et le modèle : il faudra remettre en cause celui-ci.
Comment mesurer une distance en astronomie ?
La triangulation
Commençons par essayer de mesurer la distance d'un objet situé sur la Terre. C'est ainsi que l'on pourra cartographier la surface terrestre de proche en proche.
La méthode pour mesurer une distance est celle de la triangulation : on voit un objet dans une certaine direction (visée n°1) et si on se déplace d'une distance
appelée "base", on voit l'objet dans une direction différente (visée n°2). Dans le triangle "objet - visée n°1 - visée n°2", on connaît un côté et deux angles : on
peut calculer les autres côtés et déterminer la distance de l'objet. Cet effet est appelé "parallaxe" en astronomie.
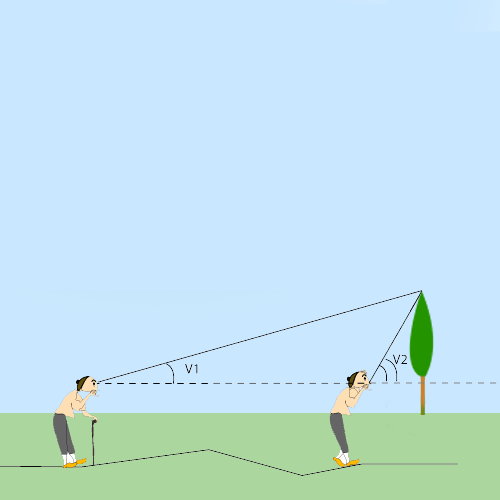
Calcul d'une distance par triangulation.
Crédit :
ASM/Jean-Eudes Arlot, Gilles Bessou et Djamila Taharbouche
La parallaxe en astronomie
Pour calculer la distance d'un corps céleste à la Terre, on procédera de la même façon. Depuis deux lieux sur Terre, on va mesurer l'angle de vue d'un astre et, connaissant la base, calculer la distance.
On conçoit bien que cette méthode a ses limites : si l'astre est très loin, la plus grande base terrestre ne pouvant dépasser 12000 kilomètres (le diamètre terrestre), il faut que la différence d'angle de visée entre les deux observateurs soit mesurable avec l'instrumentation dont les astronomes disposent. Jusqu'au XVIIème siècle, même la distance de la Lune n'était pas accessible par cette méthode.
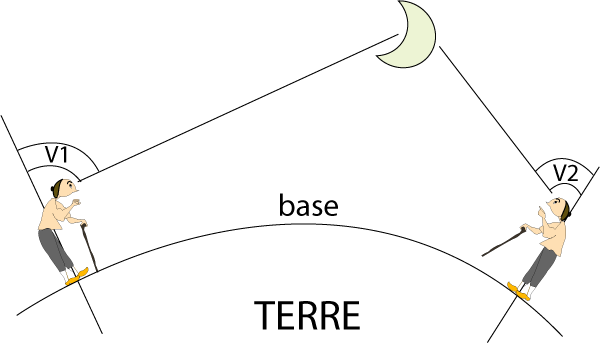
Calcul d'une distance par parallaxe.
Crédit :
ASM/Jean-Eudes Arlot, Gilles Bessou et Djamila Taharbouche
Exercice
 Calcul d'une distance par triangulation
Calcul d'une distance par triangulation
Mesure de distance par triangulation
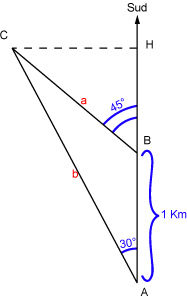
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
Question 1)
On désire mesurer la distance CH entre un bâtiment C et une route ABH de direction Nord-Sud sur laquelle se déplace un observateur qui ne peut mesurer que des angles ou des distances sur la route. D'une position A, l'observateur mesure un angle d'azimuth 30° entre le bâtiment C et la direction du Sud. D'une position B située un kilomètre plus loin sur la route, l'observateur va mesurer un azimuth de 45°.
Pour calculer la distance CH, il suffit de résoudre le triangle ABC connaissant les deux angles en A et B et la base AB. On applique une des relations entre angles et côtés dans un triangle.
Rappel : dans un triangle quelconque ABC, on a la relation :
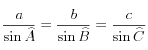
La mesure par la parallaxe
L'image ci-contre montre le principe de détermination de la distance Terre-Lune par la parallaxe (on connaît D et le rayon terrestre et on mesure α et β). Comme nous l'avons vu précédemment, il est impératif de disposer d'instruments capables de mesurer une différence entre les angles α et β. Cela limite la distance à la Terre mesurable.
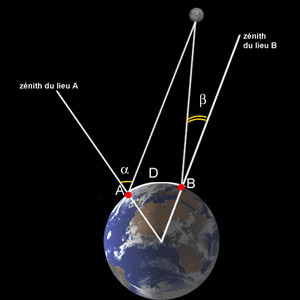
Principe de la mesure de la distance Terre-Lune par triangulation
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou + images NASA
En savoir plus: la parallaxe horizontale
 En savoir plus
En savoir plus
On a vu précédemment que triangulation ou parallaxe utilisait le même principe pour déterminer la distance d'un objet éloigné sans avoir à y aller et sans mesurer directement la distance à l'objet. On remarque que la précision de la mesure dépend de la longueur de la base. Il faut pouvoir mesurer les angles avec suffisamment de précision. Pour un astre pas trop éloigné, il suffit de se déplacer sur la surface de la Terre -ou mieux de faire deux observations simultanées à partir de deux lieux éloignés sur la surface de la Terre- pour en déterminer la distance. C'est tout à fait faisable pour la Lune qui est proche avec nos instruments de mesure actuels.
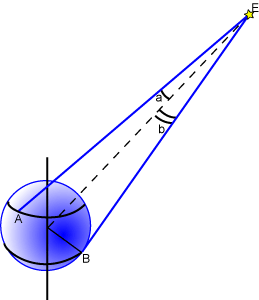
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
On remarque alors que le mouvement diurne de rotation de la Terre autour de son axe déplace chaque observateur au cours de la journée. Ce déplacement va modifier l'angle sous lequel on voit un astre à distance finie par rapport à l'angle de vue depuis le centre de la Terre qui ne bouge pas. C'est la parallaxe diurne. La distance séparant deux positions d'un observateur peut servir de "base" pour mesurer une distance. Cependant, une telle base a une valeur limite maximale : c'est le diamètre terrestre.
On appellera "parallaxe horizontale d'un astre", la valeur maximale de la parallaxe diurne de cet astre. Elle sera atteinte pour un astre observé à l'horizon. Cette valeur est donc l'angle sous lequel un observateur situé sur l'astre en question voit le rayon terrestre.
On verra plus loin que le déplacement de la Terre autour du Soleil va servir de base pour la parallaxe annuelle.
Mesure de la distance Terre-Soleil et Terre-Planètes
La méthode de triangulation précédente devrait pouvoir être appliquée à tous les corps du système solaire. Mais pour le Soleil, c'est très difficile : il n'est pas facile à observer et il est beaucoup plus loin que la Lune (400 fois, voir figure). Pour le Soleil et les objets du système solaire éloignés, on ne peut pas appliquer simplement la méthode des parallaxes car les mesures précises d'angles ont des limites : il faut prendre en compte la réalisation des mesures pour laquelle la grandeur de la base n'est pas forcément suffisante. Le principe de la parallaxe et du calcul de triangulation est simple mais il n'est pas applicable aux astres éloignés. Nous verrons que nous aurons besoin d'un nouveau modèle théorique pour mesurer certaines distances et en déduire celles qui ne
sont pas accessibles directement à la mesure. Les lois de Kepler et la mécanique céleste seront nécessaires pour la détermination des distances dans le système solaire.

Crédit :
CNRS/Jean-Eudes Arlot
La nécessité d'un modèle théorique en astronomie
Le principe de mesure de distance présenté dans la section précédente n'est pas suffisant pour connaître toutes les distances dans le système solaire, loin de là. En effet, ce principe appliqué naïvement au Soleil en supposant que la Terre est plate, nous donne une distance du Soleil à la Terre de 6500 kilomètres !
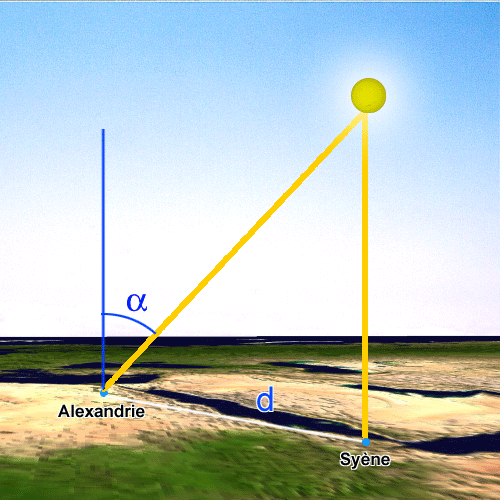
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou + image NASA
Ce type de mesure a probablement été réalisé dans l'antiquité. Anaxagore (4ème siècle avant J.-C.) calcule une taille d'environ 60 kilomètres pour le Soleil, ce qui le met à 6500 kilomètres de la Terre. Il a donc fait un calcul sur une base fausse. Pour calculer les distances dans le système solaire, il faut donc avoir de bonnes hypothèses, c'est-à-dire un modèle théorique de ce que l'on cherche à mesurer.
Premier modèle indispensable : la Terre est ronde et le Soleil est loin...
Exercice
 Calcul d'une distance par triangulation
Calcul d'une distance par triangulation
Question 1)
Expliquer en détail le raisonnement supposé d'Anaxagore qui lui fait dire que le Soleil est à 6500km et qu'il mesure environ 60 kilomètres de diamètre.
La distance Alexandrie-Syène est de 5000 stades soit 800 km. L'angle zénith-observateur-Soleil mesuré depuis Alexandrie est de 7°.
Le diamètre apparent du soleil est 0,5°.
La mesure de la Terre
Comment mesurer la Terre et constater qu'elle est ronde ? Sa rotondité est facilement compréhensible et deux faits avaient amené les astronomes de l'antiquité à admettre cette rotondité. D'abord, lors de l'observation des éclipses de Lune, l'ombre de la Terre est circulaire. Mais cette constatation pouvait aussi bien signifier que la Terre était plate avec une forme de disque. C'est la disparition progressive des navires sous l'horizon qui suggère bien que la Terre
est ronde. Comment maintenant mesurer le rayon de la Terre ?
La première mesure a été celle d'Eratosthène (vers 285-194 avant J.C.) durant l'antiquité grecque. Il avait constaté que les rayons du Soleil étaient parallèles, du moins que le Soleil était très loin sinon à l'infini. Il avait constaté que le jour du solstice, à midi, les objets n'avaient pas d'ombre à Syène (aujourd'hui Assouan) et que l'on pouvait observer le Soleil au fond d'un puits. Ce phénomène n'avait pas lieu à Alexandrie 800 km plus au Nord. Eratosthène mesura donc l'ombre portée d'un bâton à Alexandrie le jour du solstice . Il lui fallait aussi mesurer la distance Alexandrie-Syène (5000 stades) ce qui n'allait pas de soi à cette époque. Cette mesure n'était pas interprétée comme un calcul de triangulation prouvant que le Soleil était proche car il fallait se déplacer dans la direction Nord-Sud pour constater un changement de direction du Soleil. Une mesure à la même heure solaire locale (la seule disponible à l'époque) pour des lieux situés sur une ligne Est-Ouest n'aurait rien donnée (d'où la supposition que les rayons du Soleil étaient parallèles). Eratosthène ne se trompa que d'un centième sur la taille de la Terre.
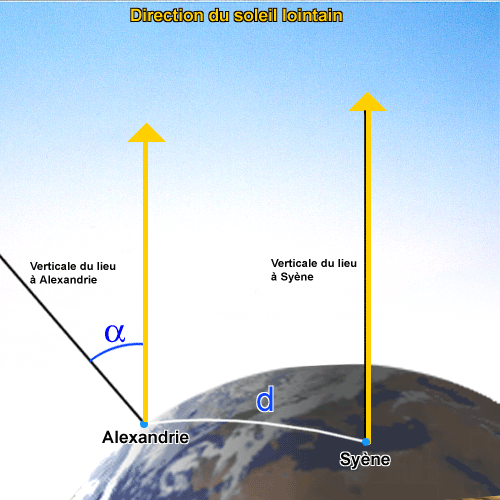
Principe des premières mesures de la taille de la Terre : le Soleil n'est pas à l'infini, mais il est suffisamment loin pour que la valeur ainsi obtenue soit très proche de la réalité
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou + image NASA
Passage d'un angle apparent à une distance
Crédit :
ASM/Jean-Eudes Arlot, Gilles Bessou et Djamila Taharbouche
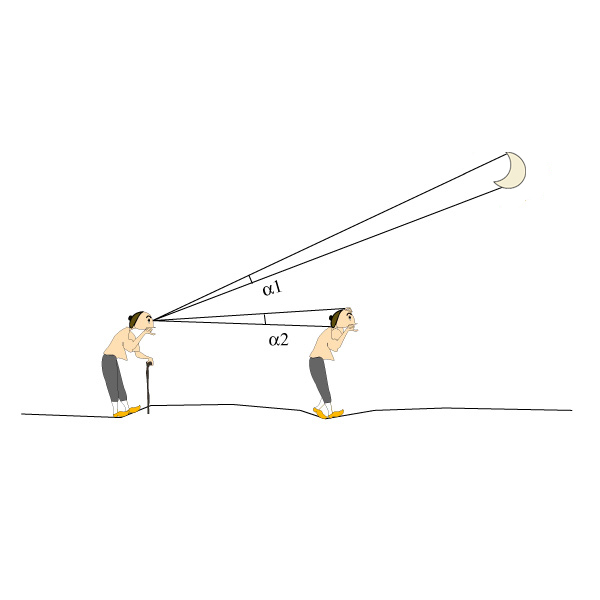
Si les deux angles α1 et α2 sont égaux, peut-on en déduire que la dimension de la Lune et celle de la tête du deuxième personnage est la même ?
Non, bien sûr...
Par contre, si α1=α2, alors distances et tailles sont liées entre elles grâce au théorème de Thalès.
Exercice
 Les distances dans le système solaire
Les distances dans le système solaire
Question 1)
La Lune et le Soleil ont à peu près le même diamètre apparent. Sachant que la Lune a un diamètre de 3475 km et se trouve à 384400 km de la Terre, quel est le diamètre du Soleil sachant qu'il se trouve à 149 600 000 km de la Terre.
Appliquer le théorème de Thalès.
La distance Terre-Lune
La mesure de la distance Terre-Lune par les éclipses
La première mesure de la taille de la Lune et de la distance Terre-Lune a été réalisée dans l'antiquité au moyen de l'observation des éclipses. L'observation des éclipses de Lune montre la largeur de l'ombre de la Terre sur la Lune et on voit que le diamètre de l'ombre de la Terre est de 2,5 diamètres lunaires au niveau de la Lune. Or, lors d'une éclipse de Soleil, la surface terrestre est au sommet du cône d'ombre puisque la zone de la Terre dans l'ombre est petite (les diamètres apparents de la Lune et du Soleil sont quasi-identiques). L'ombre de la Lune s'est donc rétrécie d'un diamètre lunaire après la distance Terre-Lune.
Il doit en être de même pour l'ombre de la Terre sur la Lune. Donc la Terre fait 2,5+1=3,5 diamètres lunaires. Connaissant le diamètre terrestre on en déduit le diamètre lunaire en kilomètres. L'angle selon lequel on voit la Lune étant d'un demi-degré (1/110 radian), la distance Terre-Lune est donc de 110 diamètres lunaires soit 60 rayons terrestres soit 384 000 km.
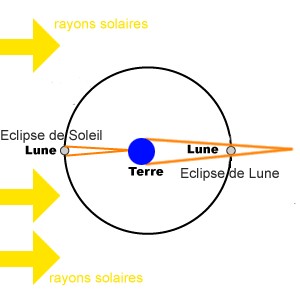
Principe de la mesure de la taille de la Lune et de la distance Terre-Lune grâce aux éclipses
Crédit :
ASM/Jean-Eudes Arlot et Gilles Bessou
Réponses aux exercices
pages_mesure-distances/mctc-exo-triangulation.html
Exercice
'Calcul d'une distance par triangulation'
- Question 1
Aide :
Pour calculer la distance CH, il suffit de résoudre le triangle ABC connaissant les deux angles en A et B et la base AB. On applique une des relations entre angles et côtés dans un triangle.
Aide :
Rappel : dans un triangle quelconque ABC, on a la relation :
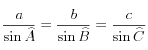
pages_mesure-distances/mctc-calcul-triangulation.html
Exercice
'Calcul d'une distance par triangulation'
- Question 1
Aide :
La distance Alexandrie-Syène est de 5000 stades soit 800 km. L'angle zénith-observateur-Soleil mesuré depuis Alexandrie est de 7°.
Aide :
Le diamètre apparent du soleil est 0,5°.
pages_mesure-distances/mctc-distances-systeme-solaire.html
Exercice
'Les distances dans le système solaire'
 Introduction
Introduction