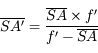Nous venons de voir quelques propriétés sur les lentilles. Nous allons pouvoir commencer à parler d'instruments astronomiques. Chouette ! Ah, mais, regardons un télescope... Horreur, de lentilles, il n'y a point ! À la place, un miroir ! Oui certes, mais nous les avons déjà vus. Quoique... celui-ci n'est pas plan... Et quand je me regarde dedans, je vois mon image grossie, parfois rétrécie, à l'envers ou à l'endroit. Non, ce miroir ne ressemble pas à ceux déjà rencontrés. Vous l'aurez compris, ce chapitre sera consacré aux miroirs dits sphériques.
Vous noterez assez vite la très forte ressemblance entre ce chapitre et le précédent.
La tête dans le tube !

Quand on regarde au fond du tube d'un télescope, on aperçoit un miroir. Ici, le fond du télescope de
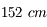
de l'observatoire de Haute-Provence.
Crédit :
B. Mollier
 Qu'est-ce qu'un miroir sphérique ?
Qu'est-ce qu'un miroir sphérique ?
Qu'est-ce qu'on appelle un miroir sphérique ? Comme son nom l'indique, c'est un miroir. C'est-à-dire une portion de verre recouverte d'une surface métallique réfléchissante. Mais nous venons de le voir dans l'introduction, il ne s'agit pas d'un miroir plan. En effet, celui-ci est découpé dans une portion sphérique de verre.
Portion de sphère
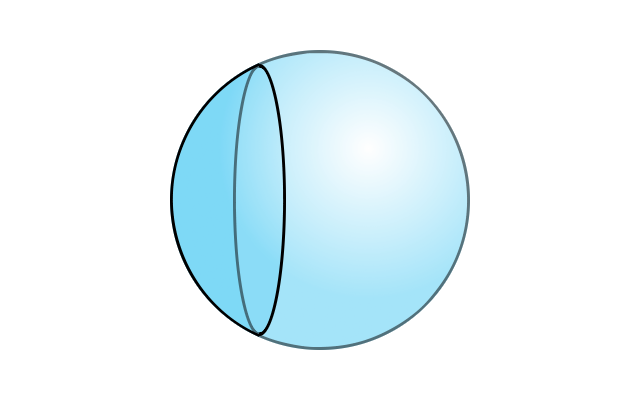
Un miroir sphérique est une portion de sphère (un morceau de boule de cristal creuse) sur laquelle est déposée une couche métallique réfléchissante.
Crédit :
ASM/B. Mollier
Portion de sphère
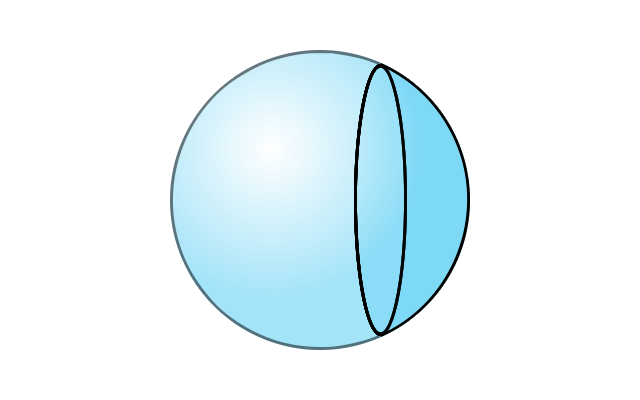
Un autre découpage possible.
Crédit :
ASM/B. Mollier
 Remarque
Remarque
En pratique, les miroirs sont rarement taillés dans des portions de sphère. Ils sont découpés dans des paraboloïdes de révolution (miroirs paraboliques) ou dans des hyperboloïdes de révolution (miroirs hyperboliques). Cependant, en première approximation, nous pourrons les considérer comme sphériques.
Miroir parabolique
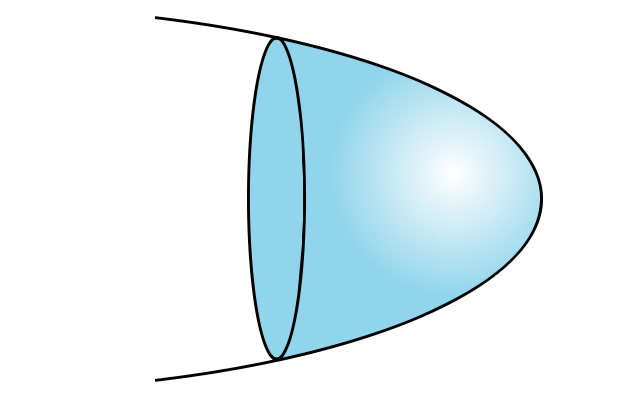
En coupant une portion d'un paraboloïde de révolution, on obtient un miroir parabolique. C'est le cas de nombreux miroirs comme les miroirs primaires des télescopes, ou la parabole pour capter le satellite.
Crédit :
ASM/B. Mollier
Miroir hyperbolique
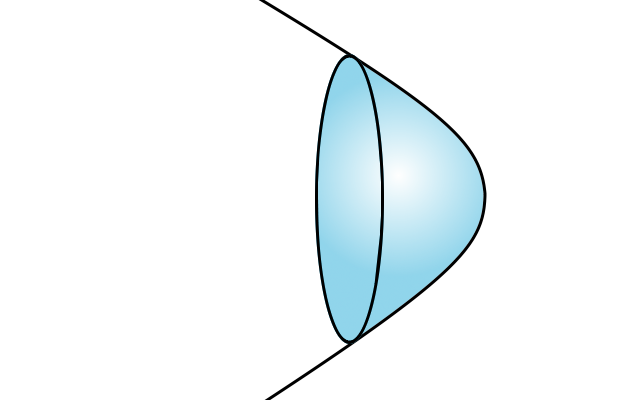
En coupant une portion d'un hyperboloïde de révolution, on obtient un miroir hyperbolique. C'est le cas de certains miroirs secondaires de télescopes.
Crédit :
ASM/B. Mollier
 Deux types de miroirs ?
Deux types de miroirs ?
On voit qu'il est possible d'aluminer soit l'intérieur, soit l'extérieur de la sphère. On obtient alors deux types de miroirs :
- Un miroir concave, si on alumine l'intérieur de la sphère
- Un miroir convexe, si on alumine l'extérieur de la sphère
Miroir concave

En aluminant l'intérieur de la sphère, on obtient un miroir concave.
Crédit :
ASM/B. Mollier
Miroir convexe
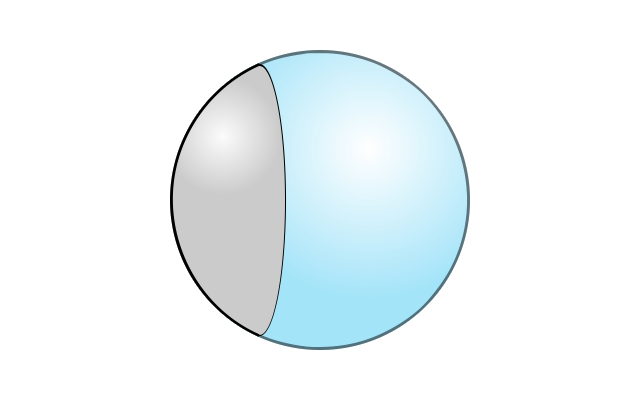
En aluminant l'extérieur de la sphère, on obtient un miroir convexe.
Crédit :
ASM/B. Mollier
 Quelques exemples
Quelques exemples
On retrouve ces miroirs dans la vie quotidienne. Les miroirs convexes par exemple, sont maintenant utilisés dans les rétroviseurs extérieurs des voitures, ou pour les miroirs que l'on dispose à la sortie des garages ou à certaines intersections où la visibilité est nulle. Les miroirs concaves se retrouvent dans certaines salles de bain ou miroirs de poche.
Miroir d'intersection

Un miroir convexe, à la sortie d'un porche, afin de pouvoir voir si un véhicule arrive.
Crédit :
B. Mollier
Miroir de salle de bain

Deux exemples de miroirs de salle de bain (pris dans un vitrine rue de Babylone à Paris). À droite, un miroir plan, comme étudié au chapitre sur les
lois de Snell-Descartes ; à gauche, un miroir concave. Notez l'inversion de l'image, à gauche, et la différence de mise au point.
Crédit :
B. Mollier
 Prenons une petite cuillère...
Prenons une petite cuillère...
Prenons une petite cuillère. Regardons-la attentivement. Son dos est convexe, son creux est concave. On a à notre disposition les deux types de miroirs.
 Y aller avec le dos de la cuillère
Y aller avec le dos de la cuillère
Si nous nous regardons dans le dos de la cuillère que voyons nous ? Notre reflet, plus petit et à l'endroit. Rapprochons ou éloignons-la. On obtient toujours la même chose.
Dos de la cuillère

Sur le dos de la cuillère, convexe, l'image est droite.
Crédit :
B. Mollier
Si on l'éclaire avec le faisceau lumineux d'une lampe torche et que l'on place un écran à proximité, on aura beau faire toutes les contorsions possibles, jamais nous n'arriverons à voir l'image de ce faisceau sur l'écran. Au contraire, il diverge.
Cela ne vous rappelle rien ? Ça ressemble un peu au comportement de la lentille divergente, non ? Alors peut-être qu'en retournant la cuillère, on retrouvera l'équivalent d'une lentille convergente...
 Le creux de la cuillère
Le creux de la cuillère
Regardons nous maintenant dans le creux de celle-ci. Ah ? Cette fois, notre reflet est à l'envers. Rapprochons-la. Notre image grossit puis se retourne. Notre reflet est à l'endroit et grossit. Bon, d'accord, ça ne marche pas avec toutes les cuillères. Il faut en général se rapprocher beaucoup et se contenter de l'image de notre oeil. Dans ce cas, prenez un miroir de poche.
Creux de la cuillère

Dans le creux de la cuillère, concave, l'image est inversée.
Crédit :
B. Mollier
Et si on reprend la lampe torche, cette fois, le faisceau converge et on peut en faire l'image sur un écran, comme une lentille convergente.
 Conclusion
Conclusion
On vient de mettre en évidence quelques propriétés des miroirs sphériques :
- Un miroir convexe fait diverger un faisceau lumineux. Il possède un comportement similaire aux lentilles divergentes.
- Un miroir concave fait converger un faisceau lumineux. Il possède un comportement similaire aux lentilles convergentes.
 Géométrie d'un miroir sphérique
Géométrie d'un miroir sphérique
Un miroir sphérique est découpé dans une sphère. Appelons 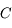 le centre de cette dernière.
le centre de cette dernière.
Notons au passage le point 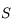 , sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.
, sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.
Centre et sommet d'un miroir sphérique
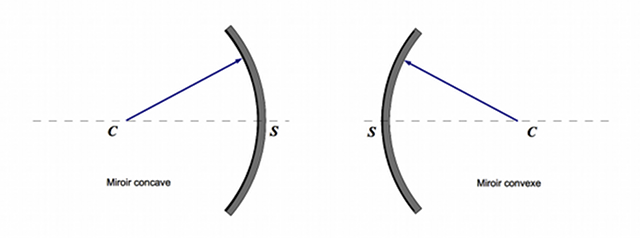
Le centre
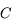
du miroir est le centre de la sphère dans laquelle il est découpé. Il est en avant du miroir dans le cas du miroir concave, en arrière dans le cas convexe. Le sommet
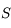
du miroir est l'intersection de l'axe optique avec celui-ci.
Crédit :
ASM/B. Mollier
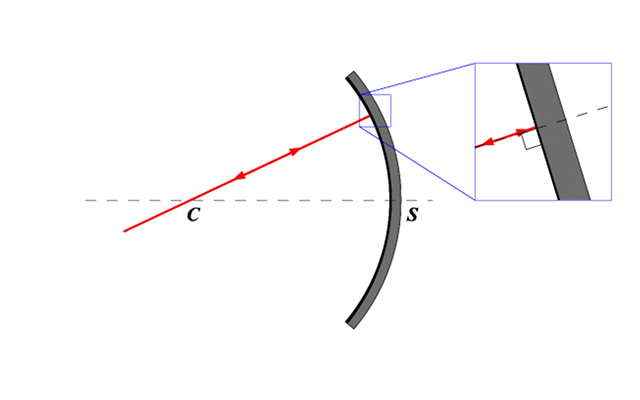
 Propriété des rayons passant par le centre C
Propriété des rayons passant par le centre C
Tout rayon lumineux passant par le centre 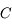 du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.
du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.
Rayon passant par le centre
Un rayon passant par le centre revient par le même chemin.
Crédit :
ASM/B. Mollier
Bref, tout rayon incident passant par le centre 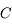 d'un miroir est confondu avec son rayon réfléchi.
d'un miroir est confondu avec son rayon réfléchi.
Considérons un faisceau parallèle (objet à l'infini) et parallèle à l'axe optique (cas du Soleil arrivant sur un miroir ardent) et observons ce qui se passe. Dans le cas d'un miroir concave (donc convergent), tous les rayons convergent en un point. Comme pour les lentilles, nous appellerons ce point foyer principal image. Ce point est l'image réelle d'un point situé à l'infini. Dans le cas d'un d'un miroir convexe, tous les rayons divergent. Cependant, ils semblent tous provenir d'un point situé derrière le miroir (il suffit de les prolonger). Nous appellerons également ce point foyer principal image. Il est l'image virtuelle d'un point situé à l'infini.
 Foyer principal image
Foyer principal image
Le foyer principal image est le point image 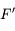 d'un point objet situé à l'infini sur l'axe optique.
d'un point objet situé à l'infini sur l'axe optique.
 Remarques
Remarques
Ce point peut être réel (cas du miroir concave) ou virtuel (cas du miroir convexe).
Par retour inverse de la lumière, si on place une source ponctuelle au foyer image, les rayons ressortiront parallèles. Il existe donc un point où si l'on place une source ponctuelle, les rayons issus de ce point seront parallèles entre eux et parallèles à l'axe optique. Ce point est appelé foyer principal objet. Il est confondu avec foyer principal image. Dans le cas d'un miroir concave, ce point est le point objet réel donnant une image à l'infini. Dans le cas d'un miroir convexe, ce point est le point objet virtuel donnant une image à l'infini.
 Définition
Définition
Le foyer principal objet est l'antécédent 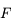 d'un point image situé à l'infini sur l'axe optique.
d'un point image situé à l'infini sur l'axe optique.
 Remarques
Remarques
Ce point peut être réel (cas du miroir concave) ou virtuel (cas du miroir convexe).
 Distance focale
Distance focale
On appelle distance focale image la distance séparant le sommet 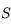 du miroir au foyer image
du miroir au foyer image 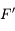 . On la note
. On la note 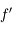 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente. 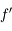 est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
Remarquons tout de suite que, comme les foyers image et objet sont confondus, la distance focale objet 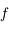 , distance entre le sommet
, distance entre le sommet 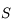 et le foyer principal objet
et le foyer principal objet 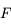 , est égale à la distance focale image
, est égale à la distance focale image 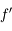 . Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.
. Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.
Distance focale
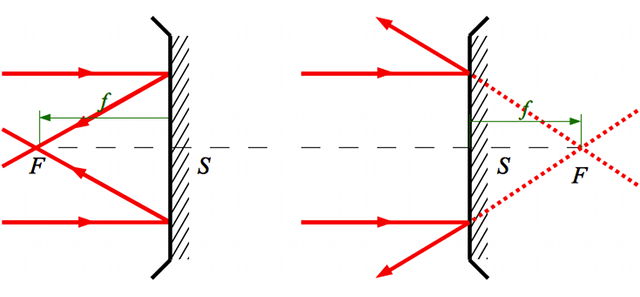
En vert, on définit la distance focale
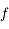
comme étant la distance du sommet
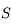
du miroir au foyer principal
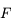
. Notez le sens de la flèche. Dans le cas d'un miroir convexe, elle est dans le même sens que celui de la propagation de la lumière incidente. Cette distance est alors positive. Dans le cas du miroir concave, cette flèche est dans le sens opposé à la propagation de la lumière incidente. Cette distance est négative. Pour plus d'informations sur ces notions de distances positives et négatives, relisez cette
page.
Crédit :
ASM/B. Mollier
 Vergence
Vergence
Comme au chapitre précédent, on définit la vergence comme étant l'inverse de la distance focale image.
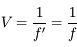
Elle s'exprime toujours en 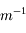 ou encore en dioptrie (noté
ou encore en dioptrie (noté 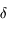 ).
).
On admet (cela se démontre) que le foyer 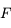 est au milieu du segment
est au milieu du segment 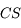
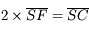
Relation entre le centre C et le foyer F
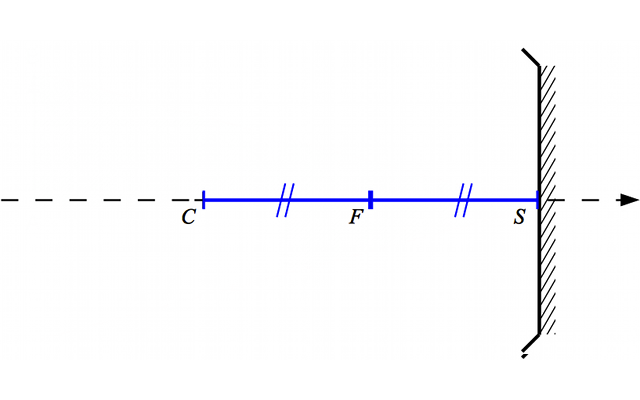
(et
) est au milieu du segment
Crédit :
ASM/B. Mollier
Considérons un faisceau de rayons parallèles mais arrivant avec une incidence par rapport à l'axe optique. Il converge en un point appartenant nécessairement au symétrique de l'axe  . Tout rayon passant par le sommet
. Tout rayon passant par le sommet  du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
Exemple de foyer secondaire dans le cas d'un miroir concave
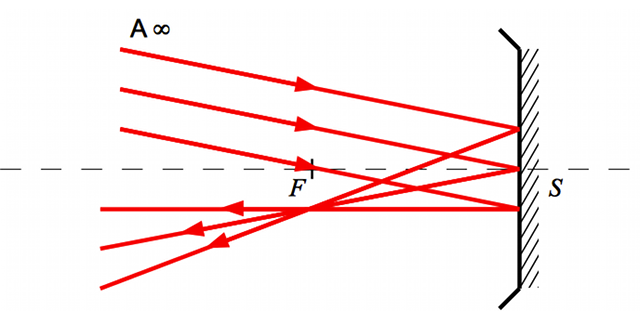
Tous les rayons qui sont parallèles entre eux convergent en un point, un foyer secondaire image, situé dans le plan focal image.
Crédit :
ASM/B. Mollier
Remarque : En fait, cette dernière remarque est vraie dans l'approximation de Gauss, qui garantit un aplanétisme approché.
Si nous faisons varier l'inclinaison du faisceau, ce point (le foyer secondaire) parcourt ce qu'on nomme le plan focal du miroir.
Pour un miroir convexe, on retrouve le même phénomène, sauf que les foyers secondaires images sont virtuels et situés derrière le miroir. Comme précédemment, nous allons pouvoir définir un foyer secondaire objet, comme étant l'antécédent d'un point image situé à l'infini, en dehors de l'axe optique. L'ensemble des foyers secondaires objets constitueront le plan focal objet.
Exemple de foyer secondaire pour un miroir convexe
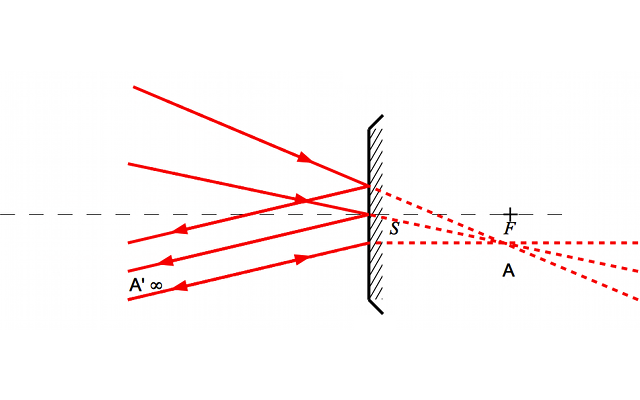
Tous les rayons issus d'un point appartenant au plan focal objet ressortent parallèles entre eux.
Crédit :
ASM/B. Mollier
Dans les conditions de Gauss, les plans focaux sont perpendiculaires à l'axe optique. Dans la vraie vie, ce sont des surfaces non planes. Les plaques photos utilisées au foyer d'un télescope de Schmidt étaient par exemple sphériques.
Avec ce que nous venons de voir, nous allons pouvoir définir quelques propriétés sur les rayons lumineux se réfléchissant sur les miroirs. Elles nous permettront d'aborder, comme au chapitre précédent, la construction des images.
- Tout rayon passant par le centre
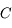 du miroir revient par le même chemin.
du miroir revient par le même chemin. - Tout rayon parallèle à l'axe optique converge au foyer principal image.
- Tout rayon passant par le foyer principal objet ressort parallèle à l'axe optique.
- Tout rayon passant par le sommet
 a pour image son symétrique par rapport à l'axe optique.
a pour image son symétrique par rapport à l'axe optique. - Deux rayons parallèles entre eux se croisent dans le plan focal image.
- Deux rayons se croisant dans le plan focal objet ressortent parallèles entre eux.
Résumé
Crédit :
ASM/B. Mollier
Arrêtons nous quelques instants sur les similitudes qu'il existe entre lentilles minces et miroirs sphériques.
Une fois n'est pas coutume, commençons par la différence. Si la lumière passant à travers une lentille se propage toujours dans le même sens, celle se réfléchissant sur le miroir repart d'où elle vient. Pour la lentille, l'espace objet et image sont situés chacun d'un côté de la lentille. Ils sont confondus pour le miroir. Mais par une vue de l'esprit, nous allons nous apercevoir que formellement ces deux systèmes sont strictement équivalents.
Un peu de pliage
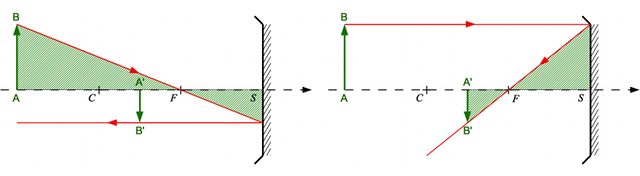
Reprenons un des dessins que nous avons faits au chapitre précédent. Celui de la lentille convergente par exemple. Plions-le le long de la lentille. Une fois plié, ce dessin ne ressemble-t-il pas comme deux gouttes d'eau à celui du miroir concave ? Et si on fait de même avec une lentille divergente, ne retrouve-t-on pas le miroir convexe ? Quand je vous disais que c'était la même chose.
Partons d'une lentille convergente...
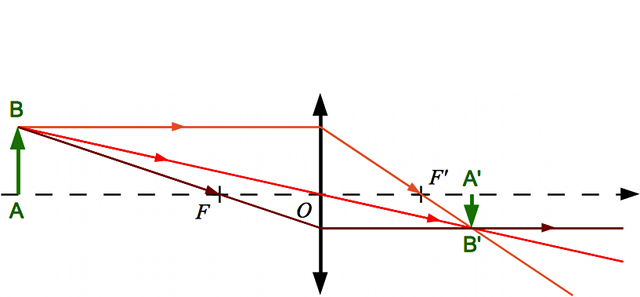
On reprend le tracé d'une image à travers une lentille convergente construit au chapitre précédent.
Crédit :
ASM/B. Mollier
... Plions le dessin...
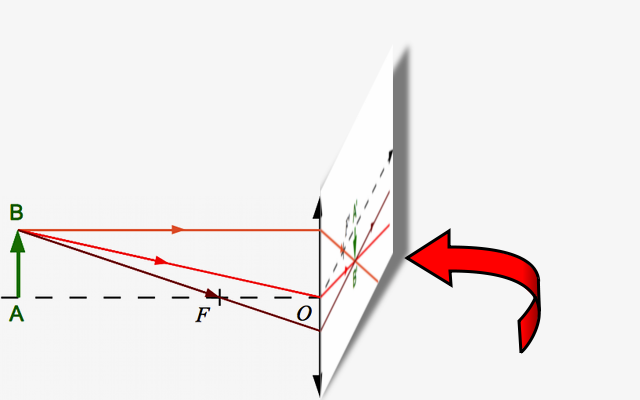
On plie le dessin le long de la lentille.
Crédit :
ASM/B. Mollier
... On obtient un miroir concave
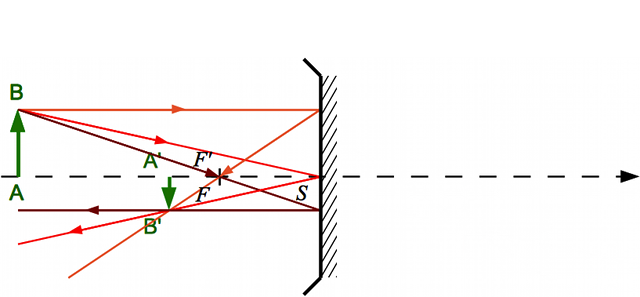
Une fois le dessin plié, les foyers se superposent, l'image passe de l'autre côté... On obtient un miroir concave.
Crédit :
ASM/B. Mollier
- En pliant notre dessin, les foyers objet et image se superposent, comme dans le cas des miroirs.
- Au moment du pliage, la distance focale image (et seulement elle) est inversée, expliquant le changement de signe par rapport au chapitre précédent. En effet, le foyer principal image passe de l'autre côté de la lentille au moment du pliage.
- Le rayon non dévié passant par le centre ? C'est désormais celui passant par le sommet.
 Espace objet/image réel/virtuel
Espace objet/image réel/virtuel
On appelle espace image réelle la zone de l'espace où l'image formée sera réelle. Dans le cas d'une lentille mince, c'est la partie de l'espace située en aval de la lentille.
On définit de la même manière l'espace image virtuelle la partie où cette image sera virtuelle. Dans le cas d'une lentille, c'est la portion de l'espace située en amont de la lentille.
En continuant ainsi, on définit également l'espace objet réel, où l'objet est réel pour le système optique, et l'espace objet virtuel où celui-ci sera virtuel. Dans le cas d'une lentille, ils se situent respectivement en amont et en aval de la lentille.
Dans le cas des miroirs sphériques, au vu de notre pliage, espaces objet réel et virtuel sont inchangés. Par contre espaces image virtuelle et réelle sont intervertis.
Espaces objet/image réel/virtuel

Où trouver un objet ou une image réelle ? virtuelle ? Pour une lentille (et un miroir sphérique), l'espace objet réel est en amont de celle-ci, l'espace objet virtuel étant en aval. Pour une lentille, l'espace image réelle est en aval et l'espace image virtuelle en amont. Dans le cas d'un miroir sphérique, ces deux derniers espaces sont inversés.
Crédit :
ASM/B. Mollier
 Philosophie des pages à venir
Philosophie des pages à venir
Nous disposons de tous les outils et de l'expérience acquise avec les lentilles pour aborder les constructions géométriques avec les miroirs sphériques. Afin d'éviter un long copier-coller, ainsi qu'un inventaire à la Prévert de tous les cas possibles, comme au chapitre précédent, je me contenterai de donner le premier exemple et laisserai en exercice les cas suivants.
 Remarques
Remarques
- L'image
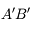 est inversée. On retrouve le cas du dos de la cuillère dans l'exemple décrit précédemment.
est inversée. On retrouve le cas du dos de la cuillère dans l'exemple décrit précédemment. - L'image
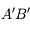 est réelle car à l'avant du miroir.
est réelle car à l'avant du miroir.
Comme promis, bah... c'est à vous de jouer ! Ah zut, il n'a pas oublié. Et non !
Auteur: B. Mollier
 Objet en aval du foyer principal objet d'un miroir concave
Objet en aval du foyer principal objet d'un miroir concave
Difficulté : ☆
Temps : 10 min
On reprend le schéma de la page précédente, mais on rapproche l'objet 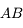 du miroir.
du miroir.
Miroir concave
Crédit :
ASM/B. Mollier
Question 1)
Au niveau de quel point ( ,
,  ou
ou 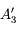 ) se situe l'image de cet objet
) se situe l'image de cet objet 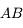 ?
?
Tracez l'image à l'aide des rayons présentés ici.
Question 2)
L'image est-elle réelle ou virtuelle ? Inversée ou non ?
Auteur: B. Mollier
 Objet réel devant un miroir convexe
Objet réel devant un miroir convexe
Difficulté : ☆☆
Temps : 10 min
On place un objet devant un miroir convexe.
Miroir convexe
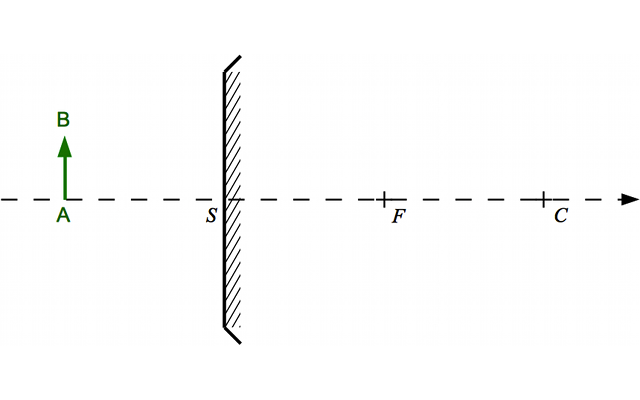
Crédit :
ASM/B. Mollier
Question 1)
Quelle est la taille de l'image 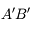 par rapport à celle de l'objet
par rapport à celle de l'objet 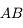 ?
?
Tracez l'image. Mesurez la ainsi que la taille de l'objet.
Comme pour les lentilles, nous allons démontrer une série de relation de conjugaison, qui nous permettront d'effectuer des calculs de position et de taille d'image.
Nous les démontrerons à partir des constructions géométriques. Puis nous les comparerons à celles obtenues pour les lentilles minces. Oui, je cherche à vous convaincre que ces deux systèmes optiques sont équivalents.
Grandissement dans le cas d'un miroir sphérique concave
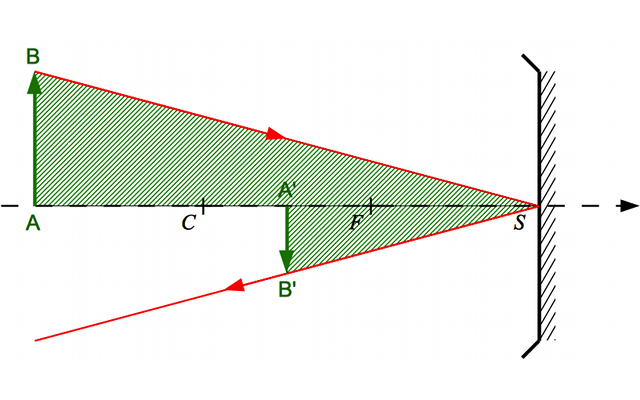
Crédit :
ASM/B. Mollier
 Expression du grandissement avec origine au sommet
Expression du grandissement avec origine au sommet
En appliquant le théorème de Thalès, on trouve immédiatement que :
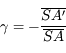
 Remarque
Remarque
Connaissant la distance de l'objet et de l'image par rapport au sommet 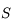 , il est donc possible de calculer la taille de l'image.
, il est donc possible de calculer la taille de l'image.
Auteur: B. Mollier
 Grandissement
Grandissement
Difficulté : ☆
Temps : 10 min
Voici trois nouvelles constructions :
Construction 1
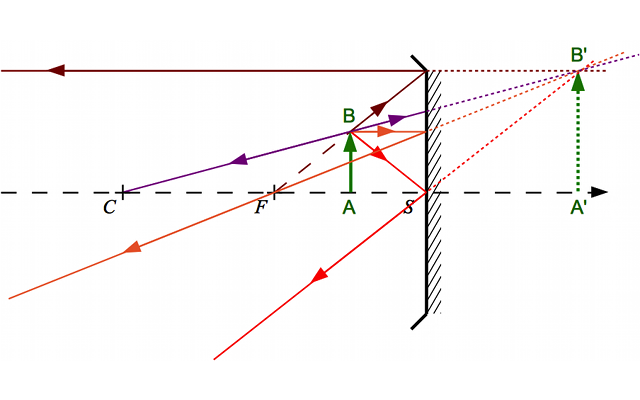
Crédit :
ASM/B. Mollier
Construction 2
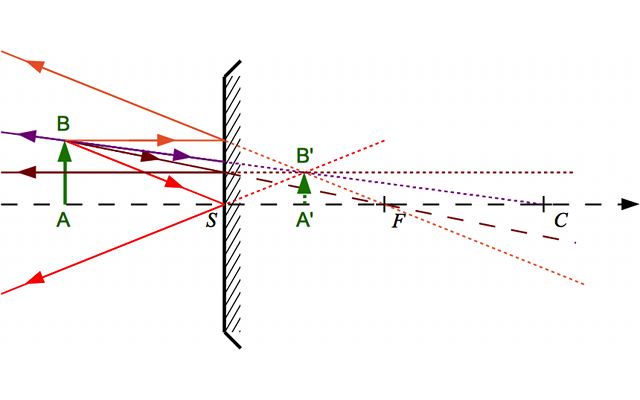
Crédit :
ASM/B. Mollier
Construction 3
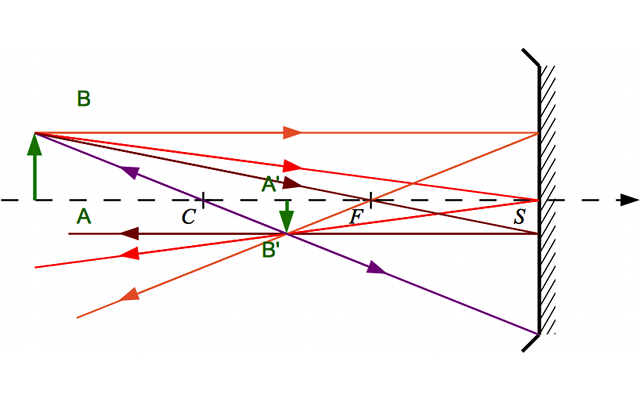
Crédit :
ASM/B. Mollier
Question 1)
Calculez le grandissement dans chacun des trois cas.
 Grandissement : origines aux foyers
Grandissement : origines aux foyers
Et si on ne connaît pas la position de l'image ? Nous allons utiliser les foyers. En appliquant cette fois-ci le théorème de Thalès deux fois avec deux rayons différents, on obtient :
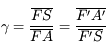
En introduisant les distances focale objet 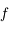 et image
et image 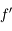 , on obtient :
, on obtient :
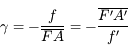
Crédit :
ASM/B. Mollier
Et voilà, connaissant la distance focale et la distance de l'objet, on peut calculer le grandissement.
 Relation de conjugaison de Newton (origines aux foyers)
Relation de conjugaison de Newton (origines aux foyers)
Remarquons qu'à partir de ces deux formules, on va pouvoir calculer la distance de l'image.
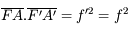
Nous venons d'établir la relation de conjugaison de Newton. Elle est aussi appelée relation de conjugaison avec origine au foyer, car les distances de l'objet et de l'image sont comptées à partir des foyers principaux.
Auteur: B. Mollier
 Narcissisme
Narcissisme
Et si on s'admirait devant un miroir ? On dispose d'un petit miroir de poche, de distance focale 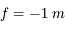 . On place notre visage à
. On place notre visage à 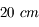 de ce dernier.
de ce dernier.
Question 1)
Quelle est la taille de notre reflet ?
Question 2)
Quelle est sa position ?
 Une autre relation de conjugaison
Une autre relation de conjugaison
Nous pouvons également obtenir une relation similaire, avec origine au sommet du miroir cette fois-ci. En partant de la formule du grandissement :
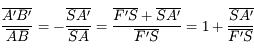
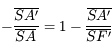
 Relation de conjugaison de Descartes (avec origine au centre)
Relation de conjugaison de Descartes (avec origine au centre)
On obtient ainsi la relation de conjugaison de Descartes :
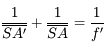
Si vous vous souvenez de la relation donnée quelques pages plus tôt : 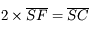 , on peut trouver d'autres relations de conjugaison.
, on peut trouver d'autres relations de conjugaison.
 Relation de conjugaison avec origine au centre
Relation de conjugaison avec origine au centre
Partant de la relation de conjugaison de Descartes, avec origine au sommet, on obtient d'abord :
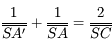
Puis en appliquant les relations de Chasles 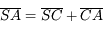 et
et 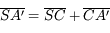 , on montre que :
, on montre que :
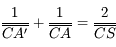
 Remarque
Remarque
On a établi plusieurs relations de conjugaison. vous n'êtes pas obligé de toutes les connaître. Une suffit. Apprenez celle avec laquelle vous vous sentez le plus à l'aise. De toutes façons, les autres se déduiront de la vôtre, ou se retrouvent à l'aide de petits dessins.
Que se passe-t-il si on prend un miroir sphérique et qu'on fait tendre son rayon de courbure vers l'infini ? Il devient plat.
Nous devrions donc pouvoir retrouver les propriétés du miroir plan à partir de celle du miroir sphérique, en faisant tendre 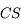 vers l'infini.
vers l'infini.
La première conséquence est que la distance focale tend également vers l'infini, puisqu'elle vaut la moitié de  .
.
Miroir plan
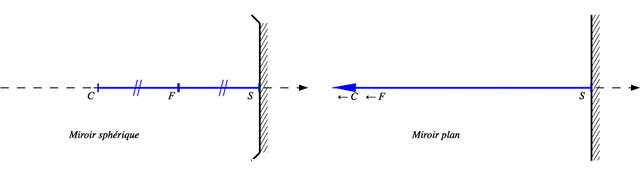
Un miroir plan est un miroir sphérique de rayon de courbure infini.
Crédit :
ASM/B. Mollier
 Position de l'image
Position de l'image
Où se situe l'image ? Prenons la relation de conjugaison de Descartes. Si la distance focale tend vers l'infini, alors 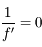 . On a donc :
. On a donc :
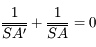
soit
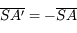 .
.
L'objet et l'image sont équidistants du miroir.
 Conclusion
Conclusion
En faisant tendre le rayon de courbure vers l'infini, nous venons de démontrer que le miroir plan possède un grandissement de 1, et que image et objet sont équidistants du miroir, autrement dit, ils sont symétriques l'un de l'autre.
 Les miroirs
Les miroirs
Nous venons de voir qu'il existait 2 types de miroirs sphériques : des miroirs concaves, comme un miroir de poche par exemple, qui ont la propriété de faire converger un faisceau lumineux ; des miroirs convexes, comme un rétroviseur, qui ont la propriété de faire diverger un faisceau lumineux.
 Tracés d'images
Tracés d'images
À l'aide de quatre rayons, il nous est désormais possible de tracer l'image d'un objet se reflétant sur le miroir. Le rayon lumineux passant par le centre revient sur lui-même, celui arrivant parallèle à l'axe optique ressort en croisant le foyer principal image, et celui passant par le foyer principal objet ressortira parallèle à l'axe optique. Enfin, le rayon frappant le miroir au sommet aura pour image son symétrique par rapport à l'axe optique.
 Relations de conjugaison
Relations de conjugaison
Enfin, nous avons quelques relations qui nous permettront de calculer des tailles d'images, les distances où elles se forment et pourquoi pas des champs de vue et des grossissements. Ce sera pour bientôt.
 BONUS : Le miroir plan
BONUS : Le miroir plan
Et on vient de voir en prime qu'un miroir plan est un miroir sphérique de rayon de courbure infini.

 de l'observatoire de Haute-Provence.
de l'observatoire de Haute-Provence.










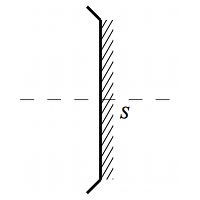 Le trait plein du côté de la métallisation, les hachures du côté du verre, les bords vers le métal.
Le trait plein du côté de la métallisation, les hachures du côté du verre, les bords vers le métal.
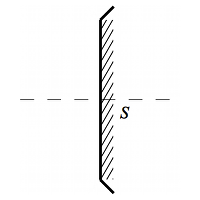 Le train plein du côté de la métallisation, les hachures du côté du verre, les bords vers le verre.
Le train plein du côté de la métallisation, les hachures du côté du verre, les bords vers le verre.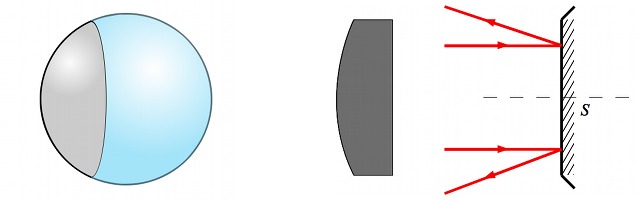
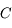 le centre de cette dernière.
le centre de cette dernière.
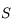 , sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.
, sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.

 du miroir est le centre de la sphère dans laquelle il est découpé. Il est en avant du miroir dans le cas du miroir concave, en arrière dans le cas convexe. Le sommet
du miroir est le centre de la sphère dans laquelle il est découpé. Il est en avant du miroir dans le cas du miroir concave, en arrière dans le cas convexe. Le sommet 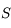 du miroir est l'intersection de l'axe optique avec celui-ci.
du miroir est l'intersection de l'axe optique avec celui-ci.
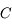 du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.
du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.

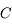 d'un miroir est confondu avec son rayon réfléchi.
d'un miroir est confondu avec son rayon réfléchi.
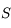 appartient à l'axe de symétrie du système. Donc, si un rayon incident arrive en
appartient à l'axe de symétrie du système. Donc, si un rayon incident arrive en 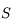 , son rayon réfléchi sera son symétrique par rapport à l'axe optique.
, son rayon réfléchi sera son symétrique par rapport à l'axe optique.
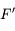 d'un point objet situé à l'infini sur l'axe optique.
d'un point objet situé à l'infini sur l'axe optique.
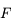 d'un point image situé à l'infini sur l'axe optique.
d'un point image situé à l'infini sur l'axe optique.
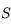 du miroir au foyer image
du miroir au foyer image 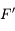 . On la note
. On la note 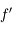 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente. 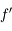 est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
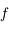 , distance entre le sommet
, distance entre le sommet 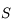 et le foyer principal objet
et le foyer principal objet 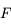 , est égale à la distance focale image
, est égale à la distance focale image 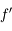 . Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.
. Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.

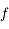 comme étant la distance du sommet
comme étant la distance du sommet 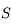 du miroir au foyer principal
du miroir au foyer principal 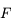 . Notez le sens de la flèche. Dans le cas d'un miroir convexe, elle est dans le même sens que celui de la propagation de la lumière incidente. Cette distance est alors positive. Dans le cas du miroir concave, cette flèche est dans le sens opposé à la propagation de la lumière incidente. Cette distance est négative. Pour plus d'informations sur ces notions de distances positives et négatives, relisez cette
. Notez le sens de la flèche. Dans le cas d'un miroir convexe, elle est dans le même sens que celui de la propagation de la lumière incidente. Cette distance est alors positive. Dans le cas du miroir concave, cette flèche est dans le sens opposé à la propagation de la lumière incidente. Cette distance est négative. Pour plus d'informations sur ces notions de distances positives et négatives, relisez cette 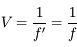
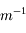 ou encore en dioptrie (noté
ou encore en dioptrie (noté 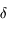 ).
).
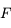 est au milieu du segment
est au milieu du segment 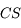
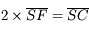
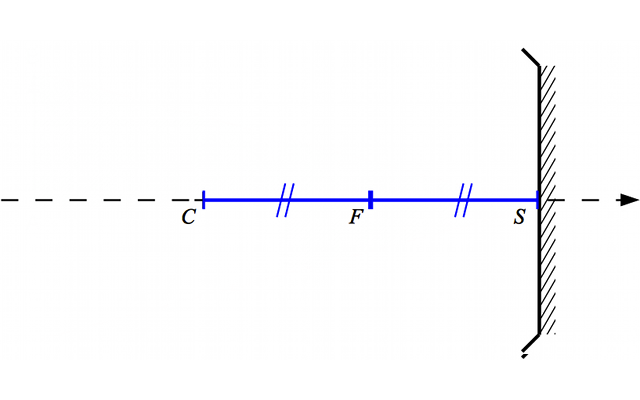
 (et
(et  ) est au milieu du segment
) est au milieu du segment 
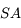 . Tout rayon passant par le sommet
. Tout rayon passant par le sommet 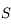 du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.


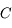 du miroir revient par le même chemin.
du miroir revient par le même chemin.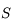 a pour image son symétrique par rapport à l'axe optique.
a pour image son symétrique par rapport à l'axe optique.




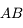 en amont d'un miroir concave et de son foyer objet. On cherche à tracer son image réfléchie.
en amont d'un miroir concave et de son foyer objet. On cherche à tracer son image réfléchie.
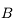 et passant par
et passant par 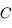 . Il revient par le même chemin.
. Il revient par le même chemin.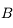 . En effet, dans les conditions de stigmatisme approché, deux rayons suffisent à définir un point image. On a le choix entre trois autres rayons. On trace par exemple le rayon issu de
. En effet, dans les conditions de stigmatisme approché, deux rayons suffisent à définir un point image. On a le choix entre trois autres rayons. On trace par exemple le rayon issu de 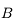 et parallèle à l'axe optique. Il se réfléchit sur le miroir en passant par le foyer principal image
et parallèle à l'axe optique. Il se réfléchit sur le miroir en passant par le foyer principal image 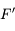 . Il croise le premier rayon en
. Il croise le premier rayon en 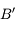 , image de
, image de 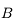 par le miroir.
par le miroir.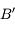 . Traçons le rayon issu de
. Traçons le rayon issu de 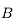 et passant par le foyer principal objet
et passant par le foyer principal objet 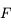 . Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point
. Il ressort parallèle à l'axe optique. On vérifie ainsi qu'il passe effectivement par le point 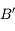
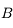 et se réfléchissant au sommet
et se réfléchissant au sommet 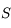 . On trace alors son symétrique par rapport à l'axe optique. Et oui, il passe également par
. On trace alors son symétrique par rapport à l'axe optique. Et oui, il passe également par 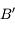 . Ouf !
. Ouf !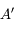 du point
du point 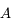 . On ne peut utiliser la même méthode que le point
. On ne peut utiliser la même méthode que le point 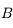 car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors ? Utilisons la propriété d'aplanétisme. Par construction,
car tous ces rayons sont identiques et confondus avec l'axe optique. Comment s'en sortir alors ? Utilisons la propriété d'aplanétisme. Par construction, 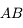 est perpendiculaire à l'axe optique. L'image
est perpendiculaire à l'axe optique. L'image 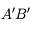 l'est également.
l'est également. 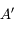 est donc le point de l'axe optique à la verticale de
est donc le point de l'axe optique à la verticale de 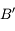 . Le tour est joué.
. Le tour est joué.
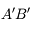 est inversée. On retrouve le cas du dos de la cuillère dans l'exemple décrit
est inversée. On retrouve le cas du dos de la cuillère dans l'exemple décrit 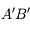 est réelle car à l'avant du miroir.
est réelle car à l'avant du miroir.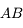 du miroir.
du miroir.

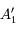 ,
, 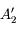 ou
ou 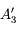 ) se situe l'image de cet objet
) se situe l'image de cet objet 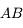 ?
?

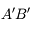 par rapport à celle de l'objet
par rapport à celle de l'objet 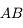 ?
?
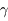 dans le cas d'un miroir sphérique est la même que pour les lentilles minces. Il s'agit du rapport entre la taille de l'image
dans le cas d'un miroir sphérique est la même que pour les lentilles minces. Il s'agit du rapport entre la taille de l'image 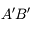 et celle de son antécédent
et celle de son antécédent 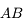 .
.
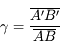

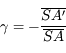
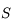 , il est donc possible de calculer la taille de l'image.
, il est donc possible de calculer la taille de l'image.


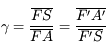
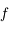 et image
et image 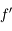 , on obtient :
, on obtient :
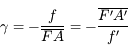

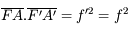
 près, elle est identique à celle des lentilles minces.
près, elle est identique à celle des lentilles minces.
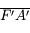 . Ce qui explique la perte du signe
. Ce qui explique la perte du signe  dans la relation de conjugaison de Newton.
dans la relation de conjugaison de Newton.
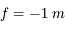 . On place notre visage à
. On place notre visage à 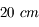 de ce dernier.
de ce dernier.
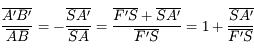
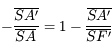
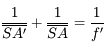
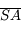 et
et 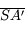 respectivement
respectivement 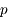 et
et 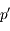 .
.
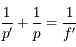
 . Le pliage, qui affecte tout ce qui se passe "à droite" de la lentille, change le signe de toutes les grandeurs algébriques situées en son aval. On change donc
. Le pliage, qui affecte tout ce qui se passe "à droite" de la lentille, change le signe de toutes les grandeurs algébriques situées en son aval. On change donc 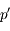 en
en 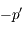 et
et 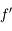 en
en 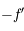 ...
...
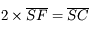 , on peut trouver d'autres relations de conjugaison.
, on peut trouver d'autres relations de conjugaison.
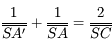
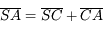 et
et 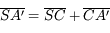 , on montre que :
, on montre que :
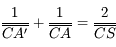
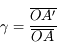
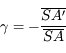
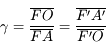
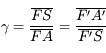
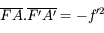
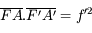
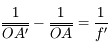
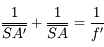
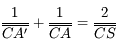
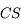 vers l'infini.
vers l'infini.
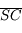 .
.

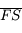 et
et 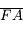 tendent vers l'infini. Or comme
tendent vers l'infini. Or comme 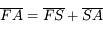 , la longueur
, la longueur 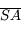 devient très vite négligeable devant les deux autres. D'où
devient très vite négligeable devant les deux autres. D'où 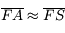 et donc le grossissement tend vers 1.
et donc le grossissement tend vers 1.
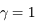
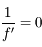 . On a donc :
. On a donc :
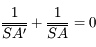
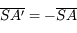 .
.
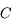 , centre de la sphère dans laquelle est découpé le miroir.
, centre de la sphère dans laquelle est découpé le miroir.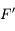 , image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet
, image d'un point situé à l'infini sur l'axe optique ; le foyer principal objet 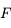 , antécédent d'un point situé à l'infini sur l'axe optique. Ils sont confondus dans le cas du miroir sphérique.
, antécédent d'un point situé à l'infini sur l'axe optique. Ils sont confondus dans le cas du miroir sphérique.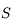 , intersection du miroir avec l'axe optique.
, intersection du miroir avec l'axe optique.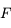 et
et 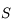 sont appelées distances focales. Ce sont des données du miroir. Elles caractérisent la vergence du miroir, c'est-à-dire son pouvoir de dévier les rayons lumineux.
sont appelées distances focales. Ce sont des données du miroir. Elles caractérisent la vergence du miroir, c'est-à-dire son pouvoir de dévier les rayons lumineux.
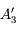 .
.
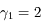
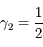
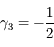
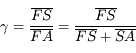
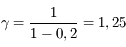
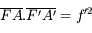
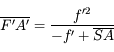
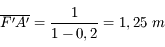
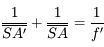 d'où
d'où