 Qu'est-ce qu'un miroir sphérique ?
Qu'est-ce qu'un miroir sphérique ?
Qu'est-ce qu'on appelle un miroir sphérique ? Comme son nom l'indique, c'est un miroir. C'est-à-dire une portion de verre recouverte d'une surface métallique réfléchissante. Mais nous venons de le voir dans l'introduction, il ne s'agit pas d'un miroir plan. En effet, celui-ci est découpé dans une portion sphérique de verre.
Portion de sphère
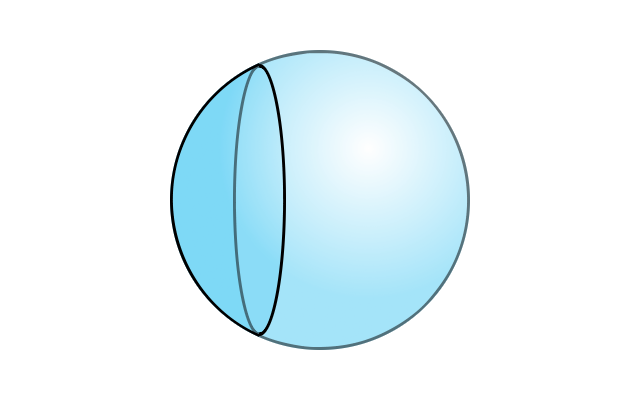
Un miroir sphérique est une portion de sphère (un morceau de boule de cristal creuse) sur laquelle est déposée une couche métallique réfléchissante.
Crédit :
ASM/B. Mollier
Portion de sphère
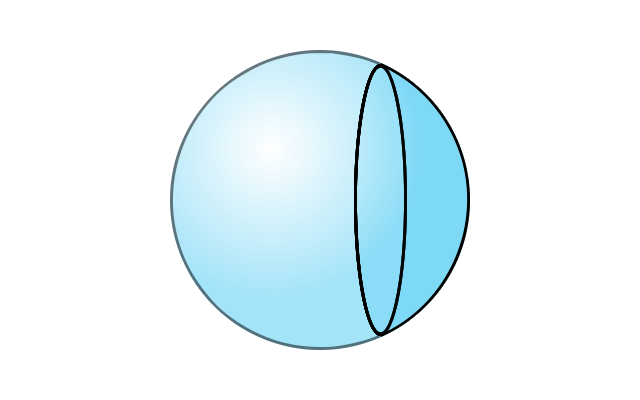
Un autre découpage possible.
Crédit :
ASM/B. Mollier
 Remarque
Remarque
En pratique, les miroirs sont rarement taillés dans des portions de sphère. Ils sont découpés dans des paraboloïdes de révolution (miroirs paraboliques) ou dans des hyperboloïdes de révolution (miroirs hyperboliques). Cependant, en première approximation, nous pourrons les considérer comme sphériques.
Miroir parabolique
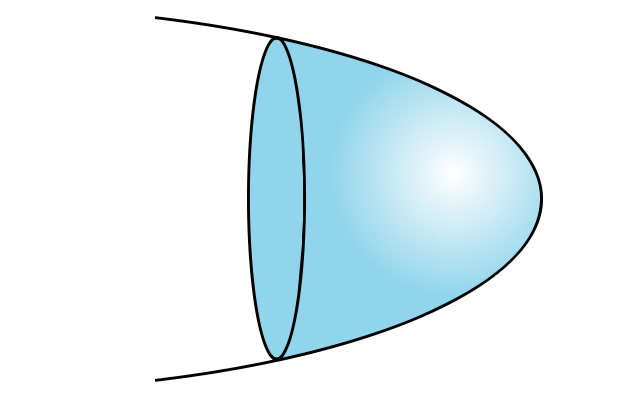
En coupant une portion d'un paraboloïde de révolution, on obtient un miroir parabolique. C'est le cas de nombreux miroirs comme les miroirs primaires des télescopes, ou la parabole pour capter le satellite.
Crédit :
ASM/B. Mollier
Miroir hyperbolique
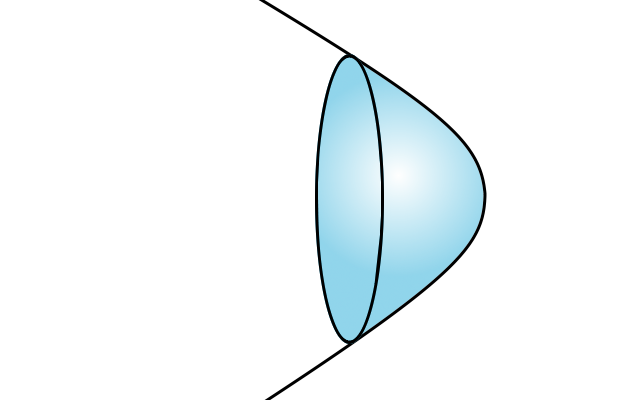
En coupant une portion d'un hyperboloïde de révolution, on obtient un miroir hyperbolique. C'est le cas de certains miroirs secondaires de télescopes.
Crédit :
ASM/B. Mollier
 Deux types de miroirs ?
Deux types de miroirs ?
On voit qu'il est possible d'aluminer soit l'intérieur, soit l'extérieur de la sphère. On obtient alors deux types de miroirs :
- Un miroir concave, si on alumine l'intérieur de la sphère
- Un miroir convexe, si on alumine l'extérieur de la sphère
Miroir concave

En aluminant l'intérieur de la sphère, on obtient un miroir concave.
Crédit :
ASM/B. Mollier
Miroir convexe
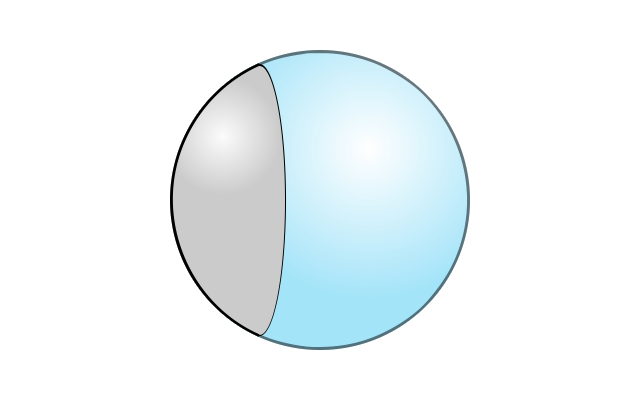
En aluminant l'extérieur de la sphère, on obtient un miroir convexe.
Crédit :
ASM/B. Mollier
 Quelques exemples
Quelques exemples
On retrouve ces miroirs dans la vie quotidienne. Les miroirs convexes par exemple, sont maintenant utilisés dans les rétroviseurs extérieurs des voitures, ou pour les miroirs que l'on dispose à la sortie des garages ou à certaines intersections où la visibilité est nulle. Les miroirs concaves se retrouvent dans certaines salles de bain ou miroirs de poche.
Miroir d'intersection

Un miroir convexe, à la sortie d'un porche, afin de pouvoir voir si un véhicule arrive.
Crédit :
B. Mollier
Miroir de salle de bain

Deux exemples de miroirs de salle de bain (pris dans un vitrine rue de Babylone à Paris). À droite, un miroir plan, comme étudié au chapitre sur les
lois de Snell-Descartes ; à gauche, un miroir concave. Notez l'inversion de l'image, à gauche, et la différence de mise au point.
Crédit :
B. Mollier
 Prenons une petite cuillère...
Prenons une petite cuillère...
Prenons une petite cuillère. Regardons-la attentivement. Son dos est convexe, son creux est concave. On a à notre disposition les deux types de miroirs.
 Y aller avec le dos de la cuillère
Y aller avec le dos de la cuillère
Si nous nous regardons dans le dos de la cuillère que voyons nous ? Notre reflet, plus petit et à l'endroit. Rapprochons ou éloignons-la. On obtient toujours la même chose.
Dos de la cuillère

Sur le dos de la cuillère, convexe, l'image est droite.
Crédit :
B. Mollier
Si on l'éclaire avec le faisceau lumineux d'une lampe torche et que l'on place un écran à proximité, on aura beau faire toutes les contorsions possibles, jamais nous n'arriverons à voir l'image de ce faisceau sur l'écran. Au contraire, il diverge.
Cela ne vous rappelle rien ? Ça ressemble un peu au comportement de la lentille divergente, non ? Alors peut-être qu'en retournant la cuillère, on retrouvera l'équivalent d'une lentille convergente...
 Le creux de la cuillère
Le creux de la cuillère
Regardons nous maintenant dans le creux de celle-ci. Ah ? Cette fois, notre reflet est à l'envers. Rapprochons-la. Notre image grossit puis se retourne. Notre reflet est à l'endroit et grossit. Bon, d'accord, ça ne marche pas avec toutes les cuillères. Il faut en général se rapprocher beaucoup et se contenter de l'image de notre oeil. Dans ce cas, prenez un miroir de poche.
Creux de la cuillère

Dans le creux de la cuillère, concave, l'image est inversée.
Crédit :
B. Mollier
Et si on reprend la lampe torche, cette fois, le faisceau converge et on peut en faire l'image sur un écran, comme une lentille convergente.
 Conclusion
Conclusion
On vient de mettre en évidence quelques propriétés des miroirs sphériques :
- Un miroir convexe fait diverger un faisceau lumineux. Il possède un comportement similaire aux lentilles divergentes.
- Un miroir concave fait converger un faisceau lumineux. Il possède un comportement similaire aux lentilles convergentes.
 Géométrie d'un miroir sphérique
Géométrie d'un miroir sphérique
Un miroir sphérique est découpé dans une sphère. Appelons 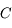 le centre de cette dernière.
le centre de cette dernière.
Notons au passage le point 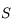 , sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.
, sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.
Centre et sommet d'un miroir sphérique
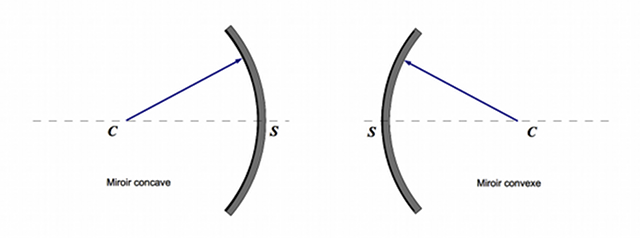
Le centre
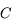
du miroir est le centre de la sphère dans laquelle il est découpé. Il est en avant du miroir dans le cas du miroir concave, en arrière dans le cas convexe. Le sommet
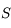
du miroir est l'intersection de l'axe optique avec celui-ci.
Crédit :
ASM/B. Mollier
 Propriété des rayons passant par le centre C
Propriété des rayons passant par le centre C
Tout rayon lumineux passant par le centre 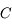 du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.
du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.
Rayon passant par le centre
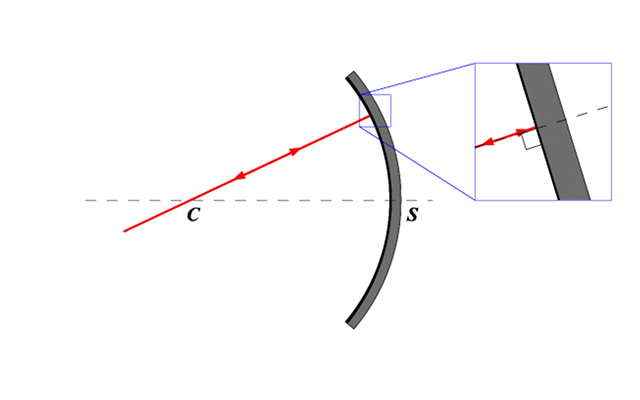
Un rayon passant par le centre revient par le même chemin.
Crédit :
ASM/B. Mollier
Bref, tout rayon incident passant par le centre 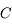 d'un miroir est confondu avec son rayon réfléchi.
d'un miroir est confondu avec son rayon réfléchi.
 Qu'est-ce qu'un miroir sphérique ?
Qu'est-ce qu'un miroir sphérique ?

 Remarque
Remarque







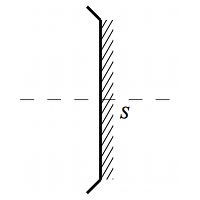 Le trait plein du côté de la métallisation, les hachures du côté du verre, les bords vers le métal.
Le trait plein du côté de la métallisation, les hachures du côté du verre, les bords vers le métal.
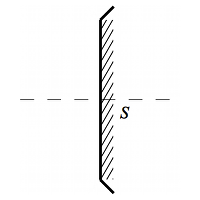 Le train plein du côté de la métallisation, les hachures du côté du verre, les bords vers le verre.
Le train plein du côté de la métallisation, les hachures du côté du verre, les bords vers le verre.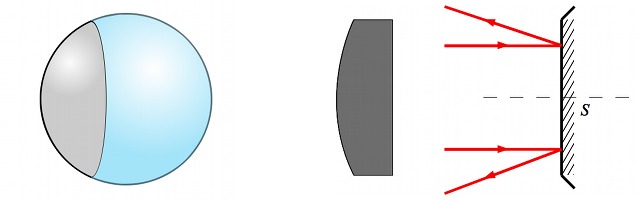
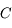 le centre de cette dernière.
le centre de cette dernière.
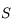 , sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.
, sommet du miroir, c'est-à-dire l'intersection de l'axe optique (l'axe de symétrie du miroir) avec le miroir.

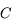 du miroir est le centre de la sphère dans laquelle il est découpé. Il est en avant du miroir dans le cas du miroir concave, en arrière dans le cas convexe. Le sommet
du miroir est le centre de la sphère dans laquelle il est découpé. Il est en avant du miroir dans le cas du miroir concave, en arrière dans le cas convexe. Le sommet 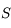 du miroir est l'intersection de l'axe optique avec celui-ci.
du miroir est l'intersection de l'axe optique avec celui-ci.
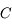 du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.
du miroir est rayon de la sphère. Que se passe-t-il quand il atteint le miroir ? Il arrive perpendiculairement à la tangente au miroir. Donc, localement, tout se passe comme si le rayon lumineux incident tombait à la verticale d'un miroir plan. Possédant un angle d'incidence nul, il repart d'où il vient (cf lois de Snell-Descartes). Il repasse par le centre.

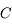 d'un miroir est confondu avec son rayon réfléchi.
d'un miroir est confondu avec son rayon réfléchi.
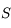 appartient à l'axe de symétrie du système. Donc, si un rayon incident arrive en
appartient à l'axe de symétrie du système. Donc, si un rayon incident arrive en 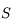 , son rayon réfléchi sera son symétrique par rapport à l'axe optique.
, son rayon réfléchi sera son symétrique par rapport à l'axe optique.