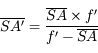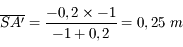Comme pour les lentilles, nous allons démontrer une série de relation de conjugaison, qui nous permettront d'effectuer des calculs de position et de taille d'image.
Nous les démontrerons à partir des constructions géométriques. Puis nous les comparerons à celles obtenues pour les lentilles minces. Oui, je cherche à vous convaincre que ces deux systèmes optiques sont équivalents.
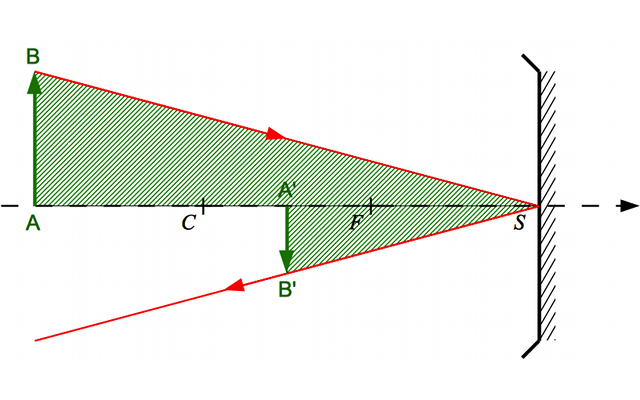
Grandissement dans le cas d'un miroir sphérique concave
Crédit :
ASM/B. Mollier
 Expression du grandissement avec origine au sommet
Expression du grandissement avec origine au sommet
En appliquant le théorème de Thalès, on trouve immédiatement que :
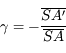
 Remarque
Remarque
Connaissant la distance de l'objet et de l'image par rapport au sommet 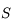 , il est donc possible de calculer la taille de l'image.
, il est donc possible de calculer la taille de l'image.
Auteur: B. Mollier
 Grandissement
Grandissement
Difficulté : ☆
Temps : 10 min
Voici trois nouvelles constructions :
Construction 1
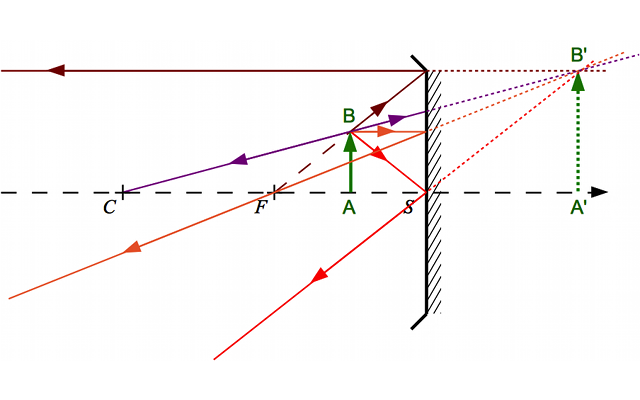
Crédit :
ASM/B. Mollier
Construction 2
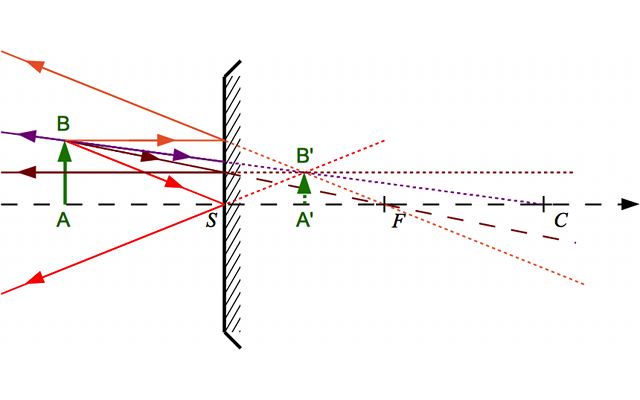
Crédit :
ASM/B. Mollier
Construction 3
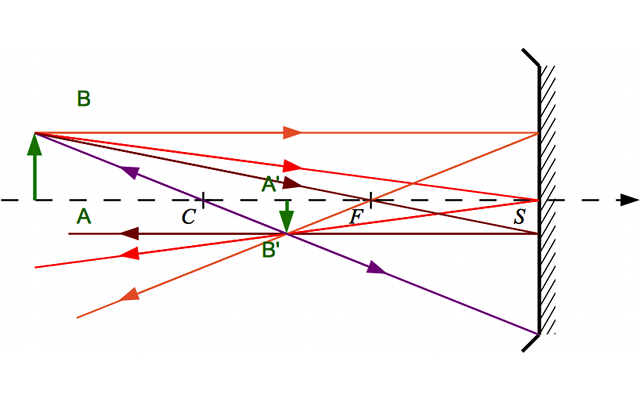
Crédit :
ASM/B. Mollier
Question 1)
Calculez le grandissement dans chacun des trois cas.
 Grandissement : origines aux foyers
Grandissement : origines aux foyers
Et si on ne connaît pas la position de l'image ? Nous allons utiliser les foyers. En appliquant cette fois-ci le théorème de Thalès deux fois avec deux rayons différents, on obtient :
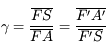
En introduisant les distances focale objet 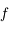 et image
et image 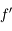 , on obtient :
, on obtient :
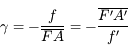
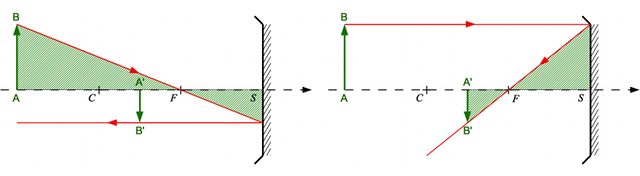
Crédit :
ASM/B. Mollier
Et voilà, connaissant la distance focale et la distance de l'objet, on peut calculer le grandissement.
 Relation de conjugaison de Newton (origines aux foyers)
Relation de conjugaison de Newton (origines aux foyers)
Remarquons qu'à partir de ces deux formules, on va pouvoir calculer la distance de l'image.
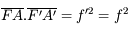
Nous venons d'établir la relation de conjugaison de Newton. Elle est aussi appelée relation de conjugaison avec origine au foyer, car les distances de l'objet et de l'image sont comptées à partir des foyers principaux.
Auteur: B. Mollier
 Narcissisme
Narcissisme
Et si on s'admirait devant un miroir ? On dispose d'un petit miroir de poche, de distance focale 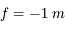 . On place notre visage à
. On place notre visage à 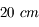 de ce dernier.
de ce dernier.
Question 1)
Quelle est la taille de notre reflet ?
Question 2)
Quelle est sa position ?
 Une autre relation de conjugaison
Une autre relation de conjugaison
Nous pouvons également obtenir une relation similaire, avec origine au sommet du miroir cette fois-ci. En partant de la formule du grandissement :
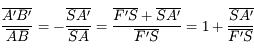
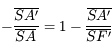
 Relation de conjugaison de Descartes (avec origine au centre)
Relation de conjugaison de Descartes (avec origine au centre)
On obtient ainsi la relation de conjugaison de Descartes :
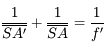
Si vous vous souvenez de la relation donnée quelques pages plus tôt : 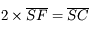 , on peut trouver d'autres relations de conjugaison.
, on peut trouver d'autres relations de conjugaison.
 Relation de conjugaison avec origine au centre
Relation de conjugaison avec origine au centre
Partant de la relation de conjugaison de Descartes, avec origine au sommet, on obtient d'abord :
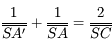
Puis en appliquant les relations de Chasles 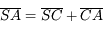 et
et 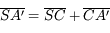 , on montre que :
, on montre que :
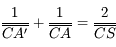
 Remarque
Remarque
On a établi plusieurs relations de conjugaison. vous n'êtes pas obligé de toutes les connaître. Une suffit. Apprenez celle avec laquelle vous vous sentez le plus à l'aise. De toutes façons, les autres se déduiront de la vôtre, ou se retrouvent à l'aide de petits dessins.
Que se passe-t-il si on prend un miroir sphérique et qu'on fait tendre son rayon de courbure vers l'infini ? Il devient plat.
Nous devrions donc pouvoir retrouver les propriétés du miroir plan à partir de celle du miroir sphérique, en faisant tendre 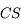 vers l'infini.
vers l'infini.
La première conséquence est que la distance focale tend également vers l'infini, puisqu'elle vaut la moitié de 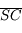 .
.
Miroir plan
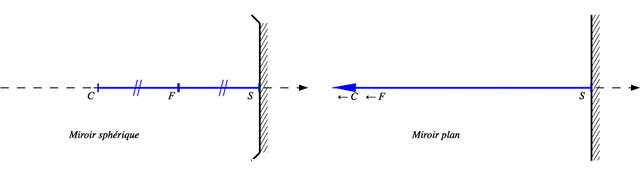
Un miroir plan est un miroir sphérique de rayon de courbure infini.
Crédit :
ASM/B. Mollier
 Position de l'image
Position de l'image
Où se situe l'image ? Prenons la relation de conjugaison de Descartes. Si la distance focale tend vers l'infini, alors 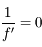 . On a donc :
. On a donc :
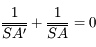
soit
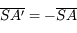 .
.
L'objet et l'image sont équidistants du miroir.
 Conclusion
Conclusion
En faisant tendre le rayon de courbure vers l'infini, nous venons de démontrer que le miroir plan possède un grandissement de 1, et que image et objet sont équidistants du miroir, autrement dit, ils sont symétriques l'un de l'autre.
 Grandissement
Grandissement dans le cas d'un miroir sphérique est la même que pour les lentilles minces. Il s'agit du rapport entre la taille de l'image
dans le cas d'un miroir sphérique est la même que pour les lentilles minces. Il s'agit du rapport entre la taille de l'image  et celle de son antécédent
et celle de son antécédent 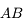 .
.
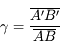

 Expression du grandissement avec origine au sommet
Expression du grandissement avec origine au sommet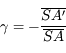
 Remarque
Remarque , il est donc possible de calculer la taille de l'image.
, il est donc possible de calculer la taille de l'image.



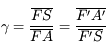
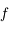 et image
et image 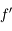 , on obtient :
, on obtient :
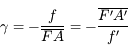

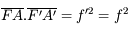
 près, elle est identique à celle des lentilles minces.
près, elle est identique à celle des lentilles minces.
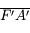 . Ce qui explique la perte du signe
. Ce qui explique la perte du signe  dans la relation de conjugaison de Newton.
dans la relation de conjugaison de Newton.
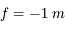 . On place notre visage à
. On place notre visage à 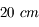 de ce dernier.
de ce dernier.
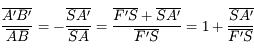
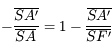
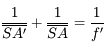
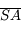 et
et 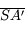 respectivement
respectivement 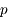 et
et 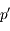 .
.
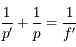
 . Le pliage, qui affecte tout ce qui se passe "à droite" de la lentille, change le signe de toutes les grandeurs algébriques situées en son aval. On change donc
. Le pliage, qui affecte tout ce qui se passe "à droite" de la lentille, change le signe de toutes les grandeurs algébriques situées en son aval. On change donc 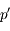 en
en 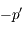 et
et 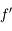 en
en 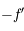 ...
...
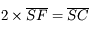 , on peut trouver d'autres relations de conjugaison.
, on peut trouver d'autres relations de conjugaison.
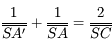
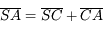 et
et 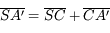 , on montre que :
, on montre que :
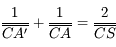
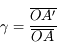
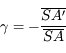
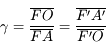
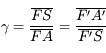
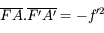
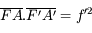
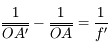
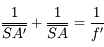
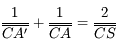
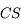 vers l'infini.
vers l'infini.
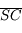 .
.

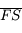 et
et 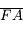 tendent vers l'infini. Or comme
tendent vers l'infini. Or comme 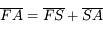 , la longueur
, la longueur 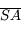 devient très vite négligeable devant les deux autres. D'où
devient très vite négligeable devant les deux autres. D'où 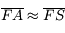 et donc le grossissement tend vers 1.
et donc le grossissement tend vers 1.
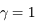
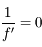 . On a donc :
. On a donc :
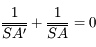
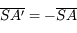 .
.
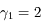
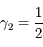
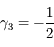
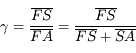
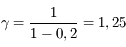
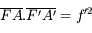
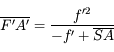
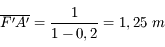
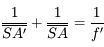 d'où
d'où