Considérons un faisceau parallèle (objet à l'infini) et parallèle à l'axe optique (cas du Soleil arrivant sur un miroir ardent) et observons ce qui se passe. Dans le cas d'un miroir concave (donc convergent), tous les rayons convergent en un point. Comme pour les lentilles, nous appellerons ce point foyer principal image. Ce point est l'image réelle d'un point situé à l'infini. Dans le cas d'un d'un miroir convexe, tous les rayons divergent. Cependant, ils semblent tous provenir d'un point situé derrière le miroir (il suffit de les prolonger). Nous appellerons également ce point foyer principal image. Il est l'image virtuelle d'un point situé à l'infini.
 Foyer principal image
Foyer principal image
Le foyer principal image est le point image 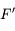 d'un point objet situé à l'infini sur l'axe optique.
d'un point objet situé à l'infini sur l'axe optique.
 Remarques
Remarques
Ce point peut être réel (cas du miroir concave) ou virtuel (cas du miroir convexe).
Par retour inverse de la lumière, si on place une source ponctuelle au foyer image, les rayons ressortiront parallèles. Il existe donc un point où si l'on place une source ponctuelle, les rayons issus de ce point seront parallèles entre eux et parallèles à l'axe optique. Ce point est appelé foyer principal objet. Il est confondu avec foyer principal image. Dans le cas d'un miroir concave, ce point est le point objet réel donnant une image à l'infini. Dans le cas d'un miroir convexe, ce point est le point objet virtuel donnant une image à l'infini.
 Définition
Définition
Le foyer principal objet est l'antécédent 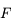 d'un point image situé à l'infini sur l'axe optique.
d'un point image situé à l'infini sur l'axe optique.
 Remarques
Remarques
Ce point peut être réel (cas du miroir concave) ou virtuel (cas du miroir convexe).
 Distance focale
Distance focale
On appelle distance focale image la distance séparant le sommet 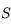 du miroir au foyer image
du miroir au foyer image 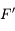 . On la note
. On la note 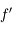 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente. 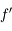 est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
Remarquons tout de suite que, comme les foyers image et objet sont confondus, la distance focale objet 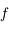 , distance entre le sommet
, distance entre le sommet 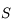 et le foyer principal objet
et le foyer principal objet 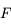 , est égale à la distance focale image
, est égale à la distance focale image 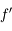 . Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.
. Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.
Distance focale
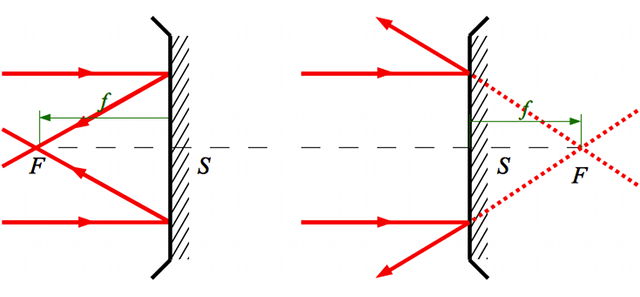
En vert, on définit la distance focale
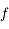
comme étant la distance du sommet
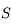
du miroir au foyer principal
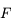
. Notez le sens de la flèche. Dans le cas d'un miroir convexe, elle est dans le même sens que celui de la propagation de la lumière incidente. Cette distance est alors positive. Dans le cas du miroir concave, cette flèche est dans le sens opposé à la propagation de la lumière incidente. Cette distance est négative. Pour plus d'informations sur ces notions de distances positives et négatives, relisez cette
page.
Crédit :
ASM/B. Mollier
 Vergence
Vergence
Comme au chapitre précédent, on définit la vergence comme étant l'inverse de la distance focale image.
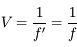
Elle s'exprime toujours en 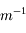 ou encore en dioptrie (noté
ou encore en dioptrie (noté 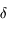 ).
).
On admet (cela se démontre) que le foyer 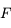 est au milieu du segment
est au milieu du segment 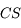
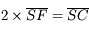
Relation entre le centre C et le foyer F
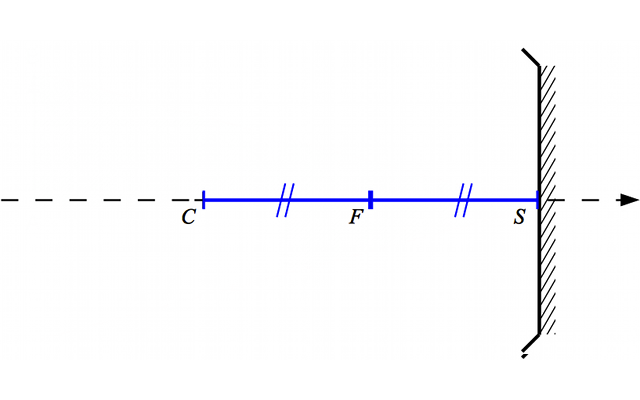
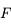
(et
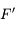
) est au milieu du segment
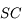
Crédit :
ASM/B. Mollier
Considérons un faisceau de rayons parallèles mais arrivant avec une incidence par rapport à l'axe optique. Il converge en un point appartenant nécessairement au symétrique de l'axe  . Tout rayon passant par le sommet
. Tout rayon passant par le sommet  du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
Exemple de foyer secondaire dans le cas d'un miroir concave
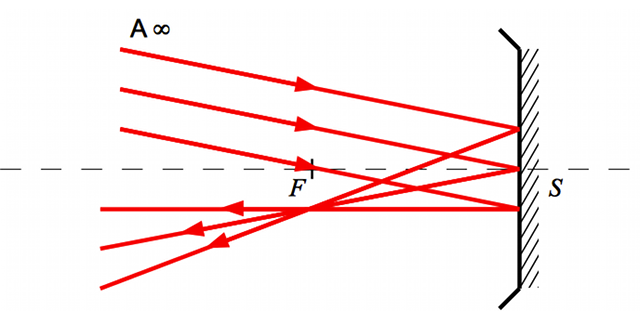
Tous les rayons qui sont parallèles entre eux convergent en un point, un foyer secondaire image, situé dans le plan focal image.
Crédit :
ASM/B. Mollier
Remarque : En fait, cette dernière remarque est vraie dans l'approximation de Gauss, qui garantit un aplanétisme approché.
Si nous faisons varier l'inclinaison du faisceau, ce point (le foyer secondaire) parcourt ce qu'on nomme le plan focal du miroir.
Pour un miroir convexe, on retrouve le même phénomène, sauf que les foyers secondaires images sont virtuels et situés derrière le miroir. Comme précédemment, nous allons pouvoir définir un foyer secondaire objet, comme étant l'antécédent d'un point image situé à l'infini, en dehors de l'axe optique. L'ensemble des foyers secondaires objets constitueront le plan focal objet.
Exemple de foyer secondaire pour un miroir convexe
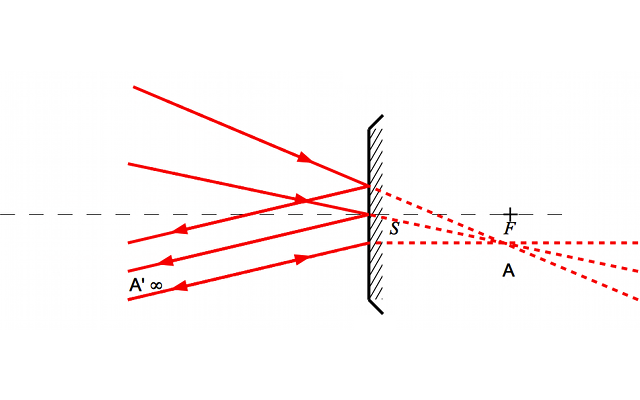
Tous les rayons issus d'un point appartenant au plan focal objet ressortent parallèles entre eux.
Crédit :
ASM/B. Mollier
Dans les conditions de Gauss, les plans focaux sont perpendiculaires à l'axe optique. Dans la vraie vie, ce sont des surfaces non planes. Les plaques photos utilisées au foyer d'un télescope de Schmidt étaient par exemple sphériques.
Avec ce que nous venons de voir, nous allons pouvoir définir quelques propriétés sur les rayons lumineux se réfléchissant sur les miroirs. Elles nous permettront d'aborder, comme au chapitre précédent, la construction des images.
- Tout rayon passant par le centre
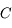 du miroir revient par le même chemin.
du miroir revient par le même chemin. - Tout rayon parallèle à l'axe optique converge au foyer principal image.
- Tout rayon passant par le foyer principal objet ressort parallèle à l'axe optique.
- Tout rayon passant par le sommet
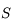 a pour image son symétrique par rapport à l'axe optique.
a pour image son symétrique par rapport à l'axe optique. - Deux rayons parallèles entre eux se croisent dans le plan focal image.
- Deux rayons se croisant dans le plan focal objet ressortent parallèles entre eux.
Résumé
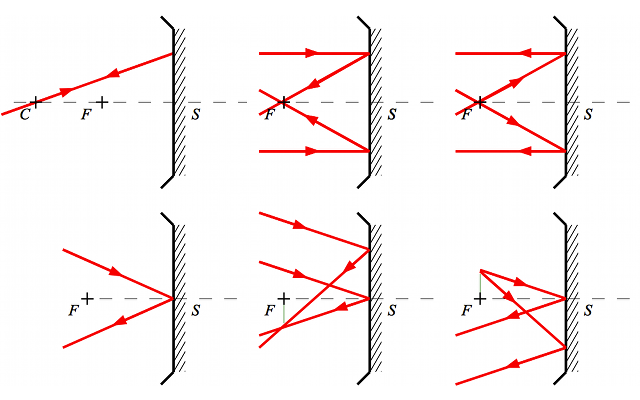
Crédit :
ASM/B. Mollier
Arrêtons nous quelques instants sur les similitudes qu'il existe entre lentilles minces et miroirs sphériques.
Une fois n'est pas coutume, commençons par la différence. Si la lumière passant à travers une lentille se propage toujours dans le même sens, celle se réfléchissant sur le miroir repart d'où elle vient. Pour la lentille, l'espace objet et image sont situés chacun d'un côté de la lentille. Ils sont confondus pour le miroir. Mais par une vue de l'esprit, nous allons nous apercevoir que formellement ces deux systèmes sont strictement équivalents.
Un peu de pliage
Reprenons un des dessins que nous avons faits au chapitre précédent. Celui de la lentille convergente par exemple. Plions-le le long de la lentille. Une fois plié, ce dessin ne ressemble-t-il pas comme deux gouttes d'eau à celui du miroir concave ? Et si on fait de même avec une lentille divergente, ne retrouve-t-on pas le miroir convexe ? Quand je vous disais que c'était la même chose.
Partons d'une lentille convergente...
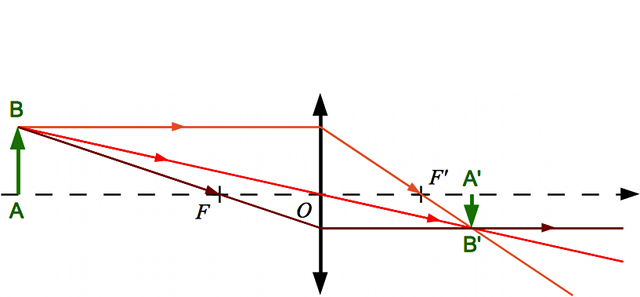
On reprend le tracé d'une image à travers une lentille convergente construit au chapitre précédent.
Crédit :
ASM/B. Mollier
... Plions le dessin...
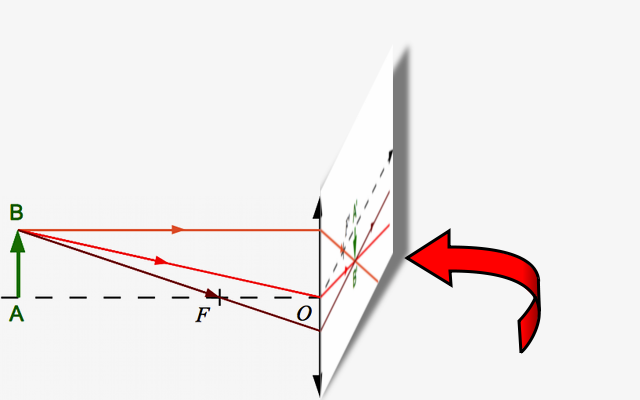
On plie le dessin le long de la lentille.
Crédit :
ASM/B. Mollier
... On obtient un miroir concave
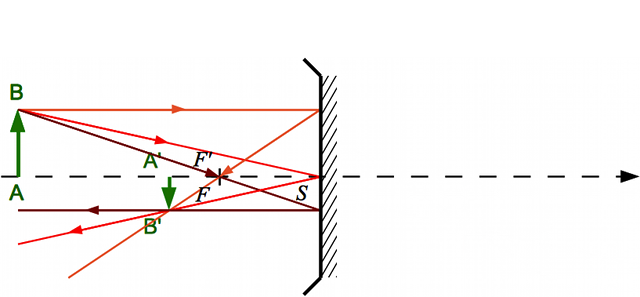
Une fois le dessin plié, les foyers se superposent, l'image passe de l'autre côté... On obtient un miroir concave.
Crédit :
ASM/B. Mollier
- En pliant notre dessin, les foyers objet et image se superposent, comme dans le cas des miroirs.
- Au moment du pliage, la distance focale image (et seulement elle) est inversée, expliquant le changement de signe par rapport au chapitre précédent. En effet, le foyer principal image passe de l'autre côté de la lentille au moment du pliage.
- Le rayon non dévié passant par le centre ? C'est désormais celui passant par le sommet.
 Espace objet/image réel/virtuel
Espace objet/image réel/virtuel
On appelle espace image réelle la zone de l'espace où l'image formée sera réelle. Dans le cas d'une lentille mince, c'est la partie de l'espace située en aval de la lentille.
On définit de la même manière l'espace image virtuelle la partie où cette image sera virtuelle. Dans le cas d'une lentille, c'est la portion de l'espace située en amont de la lentille.
En continuant ainsi, on définit également l'espace objet réel, où l'objet est réel pour le système optique, et l'espace objet virtuel où celui-ci sera virtuel. Dans le cas d'une lentille, ils se situent respectivement en amont et en aval de la lentille.
Dans le cas des miroirs sphériques, au vu de notre pliage, espaces objet réel et virtuel sont inchangés. Par contre espaces image virtuelle et réelle sont intervertis.
Espaces objet/image réel/virtuel

Où trouver un objet ou une image réelle ? virtuelle ? Pour une lentille (et un miroir sphérique), l'espace objet réel est en amont de celle-ci, l'espace objet virtuel étant en aval. Pour une lentille, l'espace image réelle est en aval et l'espace image virtuelle en amont. Dans le cas d'un miroir sphérique, ces deux derniers espaces sont inversés.
Crédit :
ASM/B. Mollier
 Foyer principal image
Foyer principal image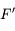 d'un point objet situé à l'infini sur l'axe optique.
d'un point objet situé à l'infini sur l'axe optique.
 Remarques
Remarques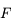 d'un point image situé à l'infini sur l'axe optique.
d'un point image situé à l'infini sur l'axe optique.
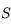 du miroir au foyer image
du miroir au foyer image 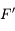 . On la note
. On la note 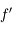 . C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente.
. C'est une quantité algébrique, c'est-à-dire qu'on la compte positivement dans le sens de propagation de la lumière incidente. 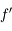 est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
est négative dans le cas d'un miroir concave, et positif dans le cas d'un miroir convexe.
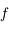 , distance entre le sommet
, distance entre le sommet 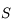 et le foyer principal objet
et le foyer principal objet 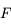 , est égale à la distance focale image
, est égale à la distance focale image 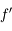 . Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.
. Nous parlerons alors indifféremment de distance focale image et objet sous le terme distance focale.

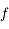 comme étant la distance du sommet
comme étant la distance du sommet 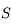 du miroir au foyer principal
du miroir au foyer principal 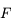 . Notez le sens de la flèche. Dans le cas d'un miroir convexe, elle est dans le même sens que celui de la propagation de la lumière incidente. Cette distance est alors positive. Dans le cas du miroir concave, cette flèche est dans le sens opposé à la propagation de la lumière incidente. Cette distance est négative. Pour plus d'informations sur ces notions de distances positives et négatives, relisez cette
. Notez le sens de la flèche. Dans le cas d'un miroir convexe, elle est dans le même sens que celui de la propagation de la lumière incidente. Cette distance est alors positive. Dans le cas du miroir concave, cette flèche est dans le sens opposé à la propagation de la lumière incidente. Cette distance est négative. Pour plus d'informations sur ces notions de distances positives et négatives, relisez cette 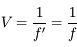
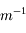 ou encore en dioptrie (noté
ou encore en dioptrie (noté 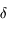 ).
).
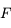 est au milieu du segment
est au milieu du segment 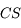
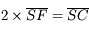
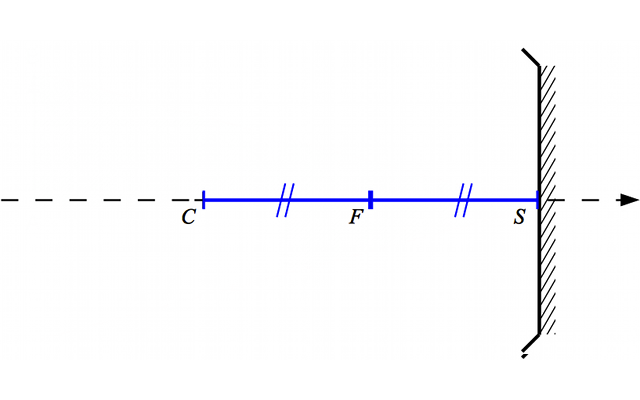
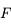 (et
(et 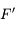 ) est au milieu du segment
) est au milieu du segment 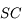
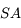 . Tout rayon passant par le sommet
. Tout rayon passant par le sommet 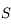 du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.
du miroir a pour image son symétrique par rapport à l'axe optique. On s'aperçoit que ce point, que nous appellerons foyer secondaire image, est à la verticale du foyer principal image.


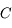 du miroir revient par le même chemin.
du miroir revient par le même chemin. a pour image son symétrique par rapport à l'axe optique.
a pour image son symétrique par rapport à l'axe optique.



