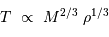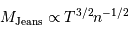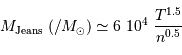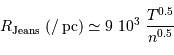Cet amas sombre, Barnard 68, à 130 pc du Soleil, se détache très
distinctement du fond stellaire en lumière visible. A la limite de
la perte d'équilibre, il est soumis aux perturbation de vents
stellaires et du rayonnement UV de jeunes étoiles. Sa température
est estimée à 16 K, sa masse à 2 masses solaires, pour un diamètre de 12500 UA.
Crédit :
ESO
Hors équilibre
L'estimation des masse, taille et densité d'un
nuage peut dévoiler qu'il
n'est pas à l'équilibre. Sa contraction va conduire à une genèse
stellaire.

Région de formation stellaire dans le Grand Nuage de Magellan.
Crédit :
ESO
Naissance multiple
La formation des étoiles est un phénomène de
groupe. Un nuage
de matière interstellaire donne naissance à de multiples étoiles.
La contraction de ce nuage est un phénomène complexe, dans un
milieu hétérogène, turbulent...
 Objectifs
Objectifs
À quelles conditions un nuage se condense-t-il ? Le critère de Jeans donne une réponse liant la masse ou le rayon limite du nuage à sa densité particulaire et sa température.
Perturbation
Un nuage s'effondre si, perturbé, son énergie mécanique devient négative :
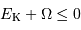
On en déduit une relation sur la masse limite du nuage, fonction de la température (pour l'agitation cinétique) et de la densité (pour la tendance à la contraction). Une masse supérieure à cette masse limite va conduire à la contraction du nuage.
On suppose le milieu homogène et uniforme, et donc le lien entre masse et rayon est simplement 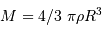 . On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
. On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
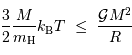
On poursuit le calcul en ne s'intéressant qu'à la dépendance en fonction des variables (ceci permet d'alléger les calculs, et de s'affranchir des constantes numériques qui ne sont de toutes façons pas correctement estimées dans une approche simplifiée). En substituant 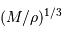 à
à 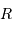 , le cas limite de l'égalité précédente donne une dépendance :
, le cas limite de l'égalité précédente donne une dépendance :
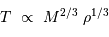
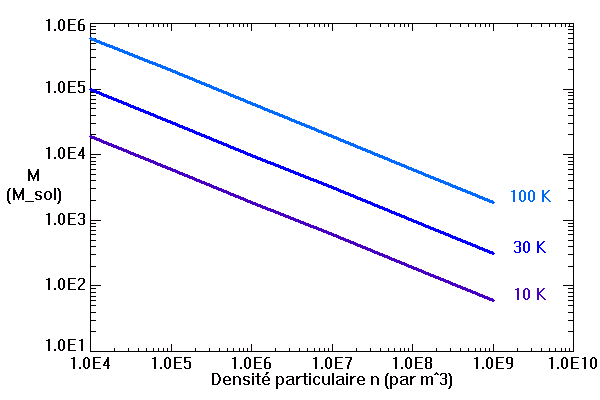
Masse de Jeans, en masse solaire, en fonction de la densité particulaire, pour 3 températures moyennes de nuage.
Crédit :
ASM
Masse de Jeans
On en déduit la masse limite du nuage, appelée masse de Jeans, qui dépend de la température et de la densité du nuage, au-delà de laquelle un nuage est amené à s'effondrer :
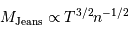
Plus le nuage est chaud, plus il peut être massif avant de s'effondrer : la pression cinétique l'aide à se maintenir. A contrario, plus il est dense, plus la masse de Jeans baisse, en raison d'un potentiel gravitationnel, attractif, croissant avec la masse.
En unité de masse solaire, la masse de Jeans devient :
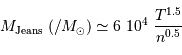
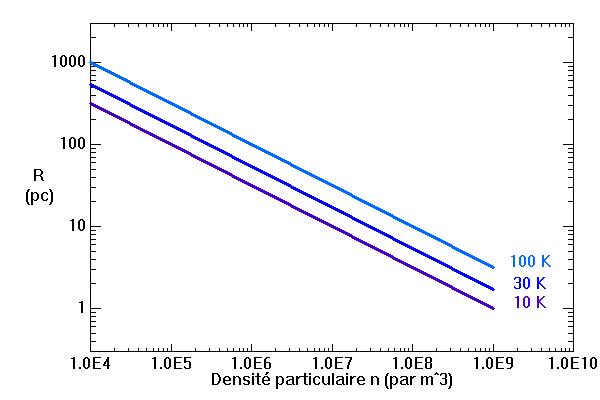
Rayon de Jeans en fonction de la densité particulaire, en parsec.
Crédit :
ASM
Rayon de Jeans
La limite d'effondrement peut également s'exprimer via le rayon du nuage, toujours en fonction de la température du nuage et de sa densité.
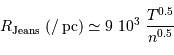

L'amas Barnard 68 n'est plus opaque dans l'infrarouge.
Crédit :
ESO
 Rayon de Jeans
Rayon de Jeans
Difficulté : ☆
Temps : 20 min
Question 1)
Exprimer le rayon de Jeans en fonction de la masse de Jeans et de la masse volumique d'un nuage.
[2 points]
Question 2)
En déduire comment le rayon de Jeans varie en fonction de la température et de la densité particulaire.
[2 points]
 Barnard 68
Barnard 68
Difficulté : ☆
Temps : 15 min
On s'intéresse au nuage Barnard 68, ici vu en infrarouge. Sa température est estimée à 16 K, sa masse à 2 fois la masse du Soleil, pour un diamètre de 12500 UA.
Question 1)
Déterminer la densité particulaire moyenne du nuage (nombre d'atome H par unité de volume).
[2 points]
Question 2)
En déduire que ce nuage est à la limite de stabilité.
[2 points]


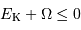
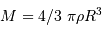 . On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
. On en déduit, quand il y a effondrement, l'inégalité sur les énergies cinétique et potentielle :
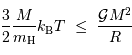
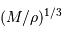 à
à 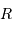 , le cas limite de l'égalité précédente donne une dépendance :
, le cas limite de l'égalité précédente donne une dépendance :