L'optique adaptative est née dans les années 1990. Elle répond à un besoin crucial : corriger, au moins pour partie, la dégradation du signal optique qui a traversé l'atmosphère.

L'optique adaptative est née dans les années 1990. Elle répond à un besoin crucial : corriger, au moins pour partie, la dégradation du signal optique qui a traversé l'atmosphère.

L'atmosphère terrestre trouble la vision que l'on a des objets célestes. Pour une étoile, cela conduit à une image scintillante, mobile. Pour un objet étendu comme le soleil, que l'on s'attend à voir tel un disque, la traversée d'une large couche atmosphérique, au lever, et encore plus au coucher en présence d'importants gradients thermiques, conduit à une image très déformée et variable.
Pour l'observation astronomique, ces perturbations sont fortement gênantes (mais on les élimine en ne menant pas d'observations sur l'horizon... sauf si les circonstances l'imposent).

Dans le vide ou tout milieu homogène, la lumière d'un objet non résolu à l'infini, par exemple une étoile, se propage comme une onde plane. Les surfaces d'onde se déplacent sans perturbation jusqu'à la pupille d'entrée du collecteur, qui transforme l'onde plane en onde sphérique.
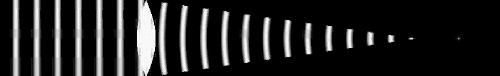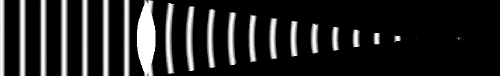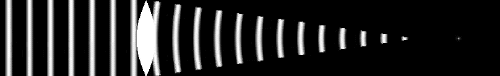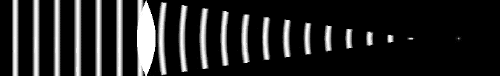
Dans un milieu inhomogène ou turbulent, les variations d'indice le long du trajet optique déphasent tout rayon par rapport à ses voisins. Ceci conduit à la déformation progressive du front d'onde collecté : initialement plan, pour un objet à l'infini, il se bosselle peu à peu.
Les variations de phase correspondant rendent la pupille partiellement incohérente. La figure de diffraction en est modifiée : des tavelures apparaissent, animées de mouvements également aléatoires.
A l'aide du simulateur ci-joint, visualiser l'effet séparé de chacune des contributions à la turbulence :

Une étoile observée à l'oeil nu scintille. Une caméra rapide permet des poses très courtes, qui vont arriver à figer la turbulence. La sommation de plusieurs de ces poses courtes conduit au phénomène de tavelures, aussi appelées "speckles": les images quasi ponctuelles, à la diffraction près, sont dispersées sur un disque bien plus large.

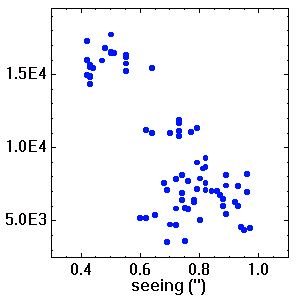
Le seeing définissant la qualité des images, il est systématiquement enregistré dans les grands sites d'observation, et les valeurs du seeing stockées parmi les multiples paramètres qui caractérisent une image.
Son évolution au cours de la nuit dépend de multiples paramètres : gradient de température, vent, humidité...
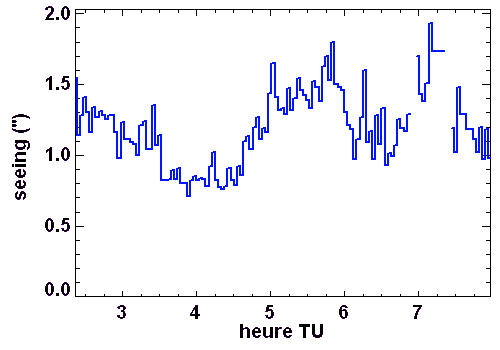
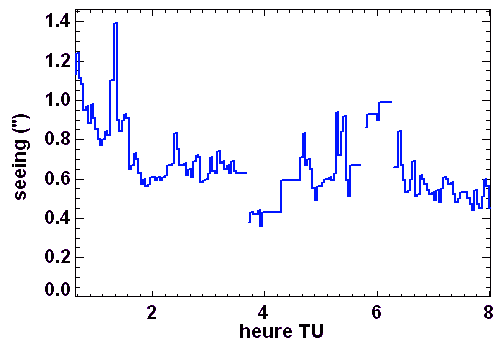
Les couches turbulentes de l'atmosphère dégradent la qualité d'image. On peut caractériser cette dégradation par différents termes :
Un bon seeing dans un bon site astronomique est de l'ordre de 0.5". Un seeing typique en lumière visible est de 1". L'ordre de grandeur du seeing mesure également celui de l'agitation.
On caractérise le seeing par un paramètre, le diamètre de cohérence 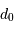 .
A cause de la turbulence, un grand télescope (de diamètre
.
A cause de la turbulence, un grand télescope (de diamètre 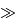
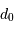 )
a une résolution angulaire identique à celle d'un télescope de diamètre
)
a une résolution angulaire identique à celle d'un télescope de diamètre 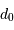 qui ne serait pas affecté par la turbulence. A la longueur d'onde
qui ne serait pas affecté par la turbulence. A la longueur d'onde 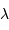 , le seeing vaut :
, le seeing vaut :
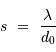
Dans le visible, un seeing moyen se caractérise par
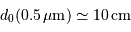 ,
et un très bon seeing par
,
et un très bon seeing par
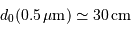 .
Le paramètre
.
Le paramètre 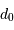 est fortement chromatique :
est fortement chromatique :
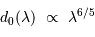
L'augmentation de 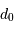 dans l'infrarouge conduit à une dégradation de l'image moindre que dans le visible.
dans l'infrarouge conduit à une dégradation de l'image moindre que dans le visible.
Le temps de cohérence associé à 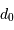 est
est 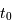 tel que :
tel que :
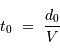
où 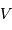 est la vitesse caractéristique du vent.
Une application numérique dans un cas moyen
est la vitesse caractéristique du vent.
Une application numérique dans un cas moyen 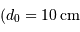 ,
, 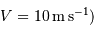 conduit à
conduit à 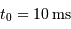 .
Le traitement de la turbulence par optique adaptative va devoir être mené plus rapidement que cette échelle de temps.
.
Le traitement de la turbulence par optique adaptative va devoir être mené plus rapidement que cette échelle de temps.
Le seeing résulte de l'agitation de l'image due à la déformation de la surface d'onde, ici visualisée sans scintillation.

A l'agitation se superpose la scintillation de l'image due à la dispersion de l'énergie, ici visualisée sans agitation.

L'agitation et la scintillation conduisent au seeing. Cette animation plus réaliste découle d'un vrai simulateur de seeing développée en laboratoire, pour tester les performances d'une optique adaptative.

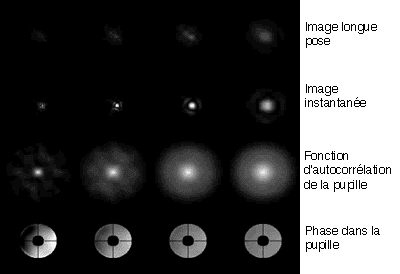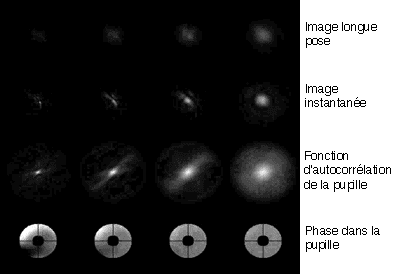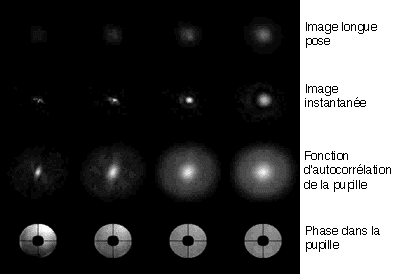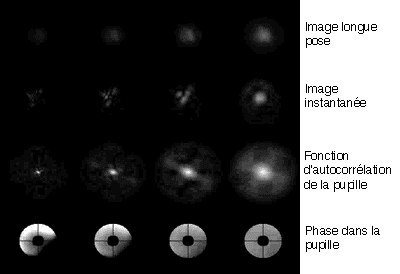
Difficulté : ☆☆ Temps : 20 min
Déterminer un ordre de grandeur d'un diamètre angulaire (étoile de type solaire à 1.3 pc, comme l'étoile voisine 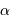 du Centaure) ou planétaire (Jupiter).
du Centaure) ou planétaire (Jupiter).
Pourquoi observe-t-on à l'oeil nu le phénomène de scintillation sur une étoile et non sur une planète ?
Difficulté : ☆☆ Temps : 40 min
Un spectromètre est nourri par une fibre qui recueille un champ de 1" sur le ciel. On s'intéresse au flux recueilli par la fibre, et on propose un modèle pour l'estimer.
Ce modèle suppose que, le seeing valant 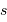 , le flux stellaire se répartit autour de l'image géométrique selon la distribution radiale :
, le flux stellaire se répartit autour de l'image géométrique selon la distribution radiale :
![\phi (r) = \phi_0 \exp\left[-{r^2\over \alpha s^2}\right]](../pages_oa/equations_seeing/equation29.png)
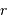 mesure l'écart angulaire à l'image géométrique ;
mesure l'écart angulaire à l'image géométrique ; 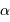 est un facteur sans dimension proche de l'unité.
est un facteur sans dimension proche de l'unité.
Déterminer le flux total 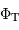 et calculer le flux reçu par une fibre qui sélectionne un rayon
et calculer le flux reçu par une fibre qui sélectionne un rayon 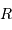 .
.
[3 points]
On souhaite étudier la fraction du signal collecté en fonction du seeing : 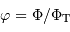 . Représenter
. Représenter 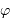 en fonction du seeing (en considérant
en fonction du seeing (en considérant 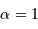 ). Expliquer le comportement pour un bon seeing ou un mauvais seeing (avec respectivement
). Expliquer le comportement pour un bon seeing ou un mauvais seeing (avec respectivement 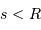 ou
ou 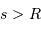 ).
).
[2 points]
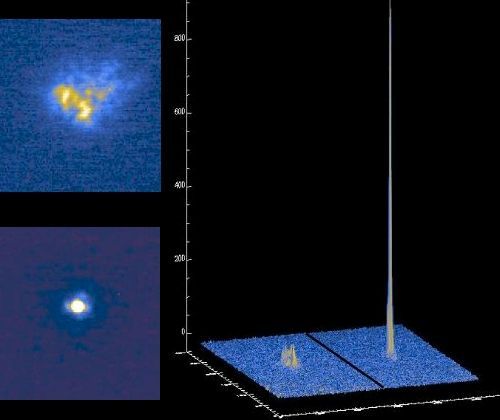

Avec un système d'optique adaptative (OA), les images sont bien mieux piquées et résolues. L'image y gagne en résolution spatiale ainsi qu'en dynamique. L'OA remet les speckles en bon ordre.
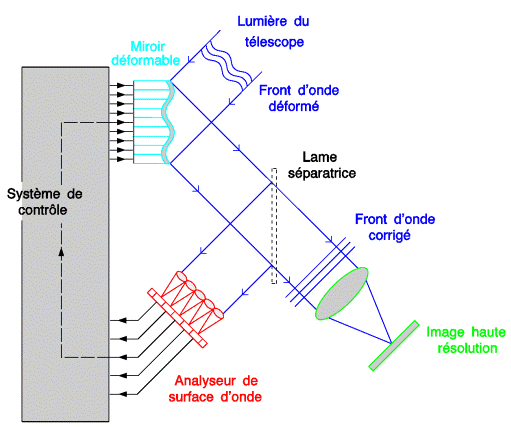
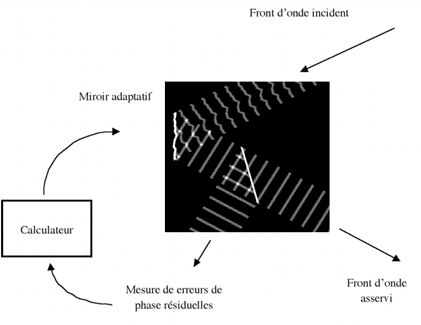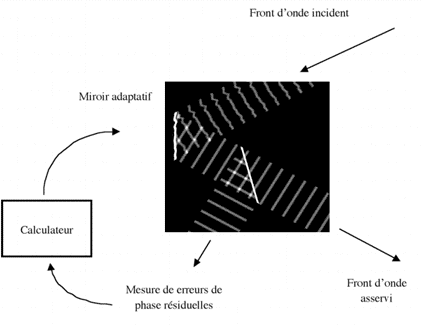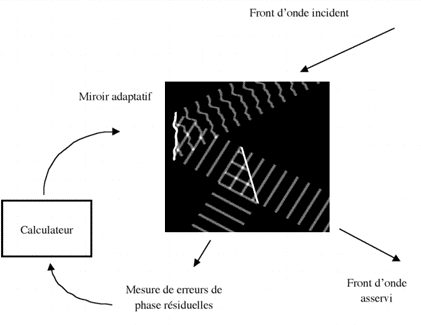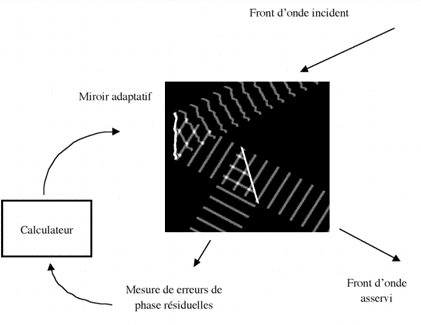
Le principe de l'optique adaptative consiste en l'analyse et correction du front d'onde, en boucle fermée. La boucle de rétroaction consiste en l'activation de senseurs commandés d'après les informations des capteurs de déformation du front d'onde.



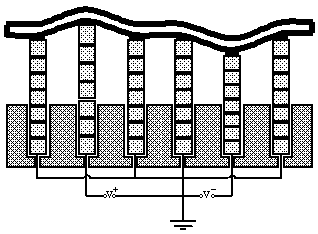
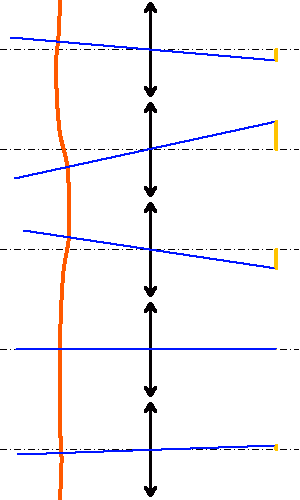
Selon que la boucle de rétroaction est ouverte ou fermée, l'OA fait son oeuvre ou non. Elle commande alors un miroir plan orientable, de correction de tip-tilt et un miroir déformable pour corriger les fréquences spatiales plus élevées.

Depuis 2001, un système d'optique adaptative est en service régulier au VLT à l'ESO, alors même que cette technique n'a émergé que dans les années 90.
Optique géométrique.
L'optique adaptative (AO) a pour but la correction en temps réel des déformations du front d'onde incident, dues à la turbulence atmosphérique, en leur opposant la contre-déformation d'un miroir déformable.
La boucle de rétroaction de l'optique adaptative comprend les éléments suivants :
L'OA permet de récupérer la tache de diffraction, de diamètre angulaire défini par le collecteur primaire. Cette performance dépend du nombre d'éléments d'images analysés sur le front d'onde, du nombre d'actuateurs mis en oeuvre, ainsi que de la fréquence de correction.

Corriger la surface d'onde en un plan d'onde idéal nécessite en général une source ponctuelle de référence, de luminosité suffisante, dans le proche voisinage de la cible étudiée.
La correction est limitée dans une région spatiale restreinte, de l'ordre de 30", et la correction est aujourd'hui réalisable dans le visible et avec d'excellentes performances dans l'infrarouge (instrument SPHERE du VLT), où les effets de la turbulence sont moindres (cf page consacrée au seeing). Le front d'onde lumineux est souvent analysé dans le visible et corrigé dans le proche IR. La correction est aujourd'hui réalisable dans le visible et avec d'excellentes performances dans l'infrarouge (instrument SPHERE du VLT), où les effets de la turbulence sont moindres (cf page consacrée au seeing). Le front d'onde lumineux est souvent analysé dans le visible et corrigé dans le proche IR.
En boucle fermée, la chaîne de rétroaction de l'optique adaptative ne mesure que les erreurs résiduelles de phase du front d'onde. La déformation du miroir doit toujours compenser toutes les erreurs.
Difficulté : ☆ Temps : 20 min
Les performances en optique adaptative à 2.2 ou 5 microns, pour le VLT (8 m), sont limitées par la diffraction du collecteur primaire. Comparer, en prenant 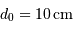 dans le visible, les résolutions angulaires avec et sans OA, et le gain apporté par l'OA.
dans le visible, les résolutions angulaires avec et sans OA, et le gain apporté par l'OA.
Pourquoi la tache image à plus courte longueur d'onde n'est-elle pas fixée par la diffraction du primaire ?

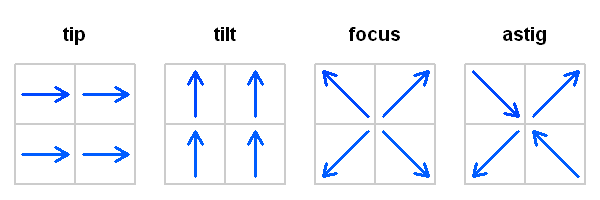
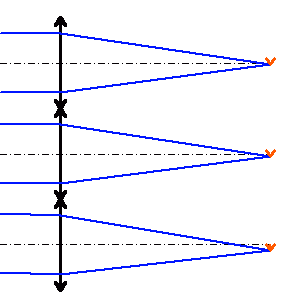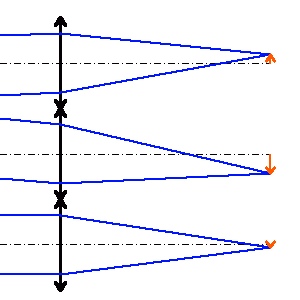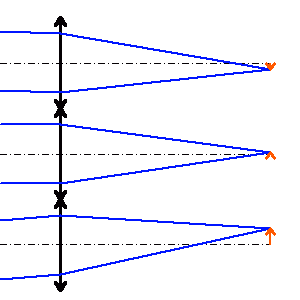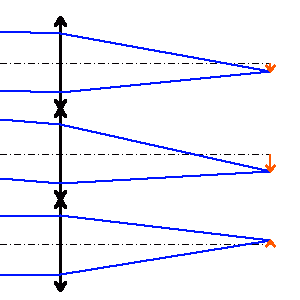
Un réseau de microlentilles assure la segmentation de la pupille en sous-pupilles. En l'absence de déformation du front d'onde, à chaque sous-pupille correspond une image centrée sur l'axe optique de la microlentille. La déformation du plan d'onde par la turbulence, et son inclinaison locale au niveau de chaque sous-pupilles, est directement retranscrite en un déplacement de l'image sous-pupillaire.
L'analyse de ces déplacements permet de remonter à la déformation du front d'onde, et se voit traduite en termes correctifs à apporter au miroir déformable.
Sur 4 quadrants, l'analyse de Shack-Hartmann permet de mettre en évidence les défauts les plus simples :
A chacune des micro-lentilles est associé un signal d'erreur.
L'optique adaptative ne sert pas qu'à faire de belles images ; l'augmentation de résolution spatiale permet aussi d'augmenter les performances spectrométriques. Maximiser le flux envoyé au travers de la fente d'un spectromètre permet de réduire la taille de la fente, et donc d'augmenter les résolutions spatiale et spectrale.

Il est possible de traiter une image observée avec OA pour retrouver cette information, en déconvoluant l'image de la PSF (fonction de transfert de l'image).

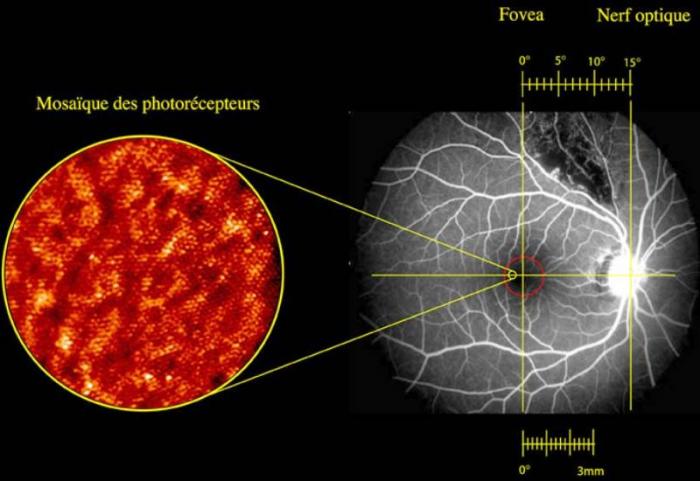
L'optique adaptative corrige les images, mais cette correction reste imparfaite. Comme elle apporte de l'information jusqu'à la limite théorique de diffraction, et donc une finesse bien au-delà du seeing, il est possible de traiter une image observée avec OA pour retrouver cette information, en déconvoluant l'image de la PSF (fonction de transfert de l'image).
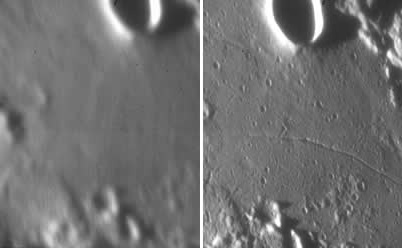
Les performances atteintes avec l'optique adaptative permettent de concurrencer les observations menées dans l'espace. La comparaison d'observations spatiales et au sol méritent d'être effectuée avec soin. Dans le cas exposé, les résultats sont semblables, le moindre diamètre du télescope Hubble étant compensé par une observation à longueur d'onde moindre également.

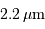 par NACO au VLT, et à
par NACO au VLT, et à 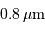 par le HST. Dans les deux cas, la résolution finale est proche de la résolution limitée par la seule diffraction. Les temps de pose sont comparables ; l'image au sol dévoile plus d'objets, essentiellement à cause de la plus grande longueur d'onde d'observation.
par le HST. Dans les deux cas, la résolution finale est proche de la résolution limitée par la seule diffraction. Les temps de pose sont comparables ; l'image au sol dévoile plus d'objets, essentiellement à cause de la plus grande longueur d'onde d'observation.
Difficulté : ☆☆ Temps : 20 min
Combien faudrait-il d'actuateurs pour corriger par OA une
pupille de 8 m, en lumière visible, avec une turbulence caractérisée par 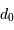 = 10cm.
= 10cm.
Comment évolue cette estimation, pour une observation menée à 2.5 micromètres.
Montrer que la fréquence de travail du système est également moins contraignante dans l'infrarouge par rapport au visible.
Difficulté : ☆☆ Temps : 20 min
L'optique adaptative au VLT, NACO, analyse le front d'onde en 144 points, et comporte 185 actuateurs.
Déterminer le diamètre caractéristique de chaque zone corrigée.
[1 points]
Déterminer l'ordre de grandeur de la longueur d'onde la plus basse potentiellement totalement corrigée. On suppose 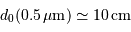 .
.
[1 points]
pages_seeing/seeing-sexercer.html
pages_oa/seeing-sexercer.html
Le Soleil 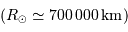 est une étoile moyenne.
Quant à Jupiter :
est une étoile moyenne.
Quant à Jupiter : 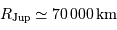 et
et
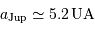 .
.
Traduire le diamètre solaire en UA peut-être utile.
Le diamètre du Soleil, traduit en UA, vaut 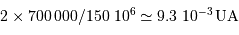 .
A 1.3 pc, le diamètre angulaire vaut donc
.
A 1.3 pc, le diamètre angulaire vaut donc 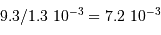 ".
".
Pour Jupiter, le diamètre angulaire vaut 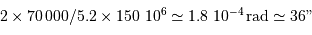 .
.
Le seeing dans le visible est de l'ordre de 1"
Les diamètres angulaires stellaire et planétaire
valent typiquement respectivement 10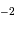 " et 40". Ces valeurs sont à comparer au seeing de l'ordre de 1".
" et 40". Ces valeurs sont à comparer au seeing de l'ordre de 1".
Il apparaît que le seeing reste bien inférieur au diamètre angulaire planétaire : l'image planétaire ne va pas être sensiblement perturbée. Autrement dit :
comme 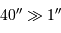 , pas de scintillation dans le cas planétaire.
, pas de scintillation dans le cas planétaire.
pages_oa/optique-adaptative-sexercer.html
Diamètre angulaire de la tache de diffraction : 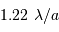
Diamètre de cohérence : 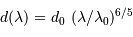
La table ci-dessous résume les résultats. Le gain comptabilise l'accroissement en résolution, qui varie comme 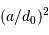 .
.
| longueur d'onde | diam cohérence | sans OA | avec OA | gain |
|---|---|---|---|---|
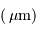 | 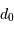 (cm) (cm) | 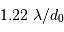 | 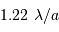 | |
| 2.2 | 60 | 0.90" | 0.067" | 183 |
| 5.0 | 150 | 0.77" | 0.152" | 25 |
Réfléchir d'une part aux caractéristiques de la turbulence, d'autre part aux propriétés de la tache de diffraction.
A plus courte longueur d'onde, d'une part la résolution ultime par la diffraction du primaire devient très fine, d'autre part le diamètre de cohérence de l'atmosphère décroît. Actuellement, les systèmes d'OA ne comportent pas assez d'actuateurs pour corriger efficacement dans le visible et le très proche IR.
pages_oa/optique-adaptative-resultats-sexercer.html
Que dit le théorème d'échantillonnage de Shannon ?
Le théorème d'échantillonnage de Shannon énonce qu'il faut 2 informations
par élément de diamètre 10 cm. Pour une pupille de diamètre 800 cm, le nombre d'actuateurs est donc de l'ordre de 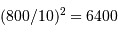 .
.
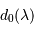 évolue comme
évolue comme 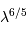
Avec une dépendance chromatique pour 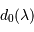 évoluant comme
évoluant comme 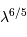 , le diamètre de cohérence passe à 70 cm. Le nombre d'actuateurs nécessaires
est alors de l'ordre de 130, ce qui est à l'heure actuelle faisable (2003).
, le diamètre de cohérence passe à 70 cm. Le nombre d'actuateurs nécessaires
est alors de l'ordre de 130, ce qui est à l'heure actuelle faisable (2003).
S'intéresser au temps de cohérence.
Le temps de cohérence évolue comme 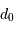 . Par conséquent, il est bien plus long dans l'infrarouge par rapport au visible, et donc la fréquence de fonctionnement de l'OA peut être moindre.
. Par conséquent, il est bien plus long dans l'infrarouge par rapport au visible, et donc la fréquence de fonctionnement de l'OA peut être moindre.