Tavelures
Une étoile observée à l'oeil nu scintille. Une caméra rapide permet des poses très courtes, qui vont arriver à figer la turbulence. La sommation de plusieurs de ces poses courtes conduit au phénomène de tavelures, aussi appelées "speckles": les images quasi ponctuelles, à la diffraction près, sont dispersées sur un disque bien plus large.

Speckles, enregistrés par lors d'une pose courte (image de gauche, en vidéo inverse) ou longue (image de droite).
Crédit :
ESO
Enregistrement du seeing
Le seeing définissant la qualité des images, il est systématiquement enregistré dans les grands sites d'observation, et les valeurs du seeing stockées parmi les multiples paramètres qui caractérisent une image.
Son évolution au cours de la nuit dépend de multiples paramètres : gradient de température, vent, humidité...
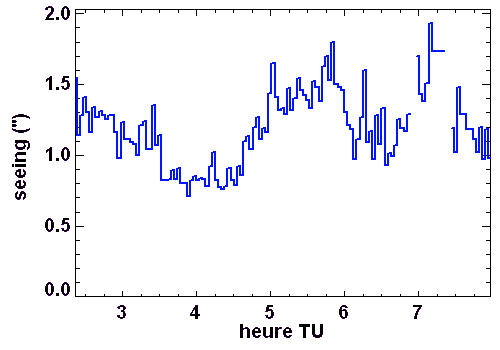
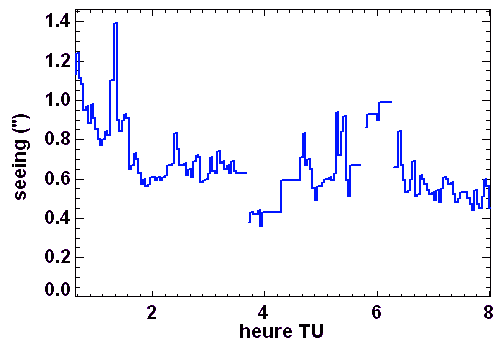
Enregistrement du seeing sur le site ESO de La Silla : une bonne nuit (seeing médian de 0.6") et une mauvaise (1.2").
Crédit :
ESO/ASM
Diverses composantes
Les couches turbulentes de l'atmosphère dégradent la qualité d'image.
On peut caractériser cette dégradation par différents termes :
- L'agitation :
la tache image se déplace, à cause des fluctuations d'indice de
l'atmosphère perturbée.
- La scintillation :
même effet que l'agitation, mais selon un point
de vue différent, où l'on ne suit pas le déplacement de la tache
image. Le flux lumineux
en un point donné est modulé dans le temps, car une partie des photons incidents a été déviée.
- Le seeing ou qualité d'image : mesure l'élargissement
de la tache image.
Agitation
Le seeing résulte de l'agitation de l'image due à la déformation de la surface d'onde, ici visualisée sans scintillation.

Effet de l'agitation sur une image stellaire, très schématisée : le barycentre de l'étoile est mobile.
Crédit :
ASM
Scintillation
A l'agitation se superpose la scintillation de l'image due à la
dispersion de l'énergie, ici visualisée sans agitation.

Effet de la scintillation sur une image stellaire, très schématisée : le flux de l'étoile est variable dans le temps.
Crédit :
ASM
Seeing
L'agitation et la scintillation conduisent au seeing.
Cette animation plus réaliste découle d'un vrai simulateur de seeing développée en laboratoire, pour tester les performances d'une optique adaptative.

Scintillation et agitation conduisent au seeing.
Crédit :
ASM
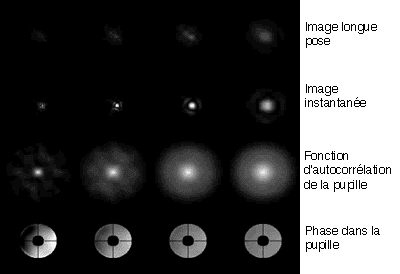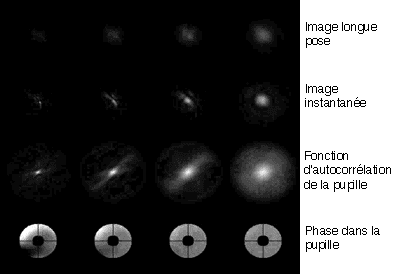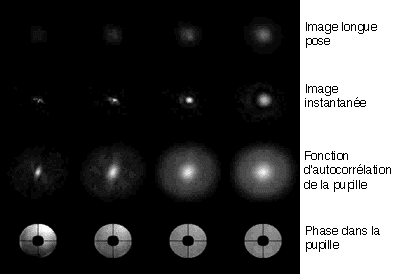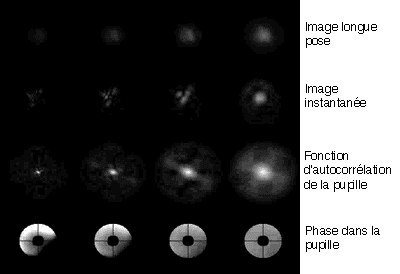
La turbulence, pour 4 valeurs de seeing. L'image est d'autant plus piquée
que la phase est uniforme, et inversement
Crédit :
Observatoire de Paris/LESIA
 Seeing
Seeing
Difficulté : ☆☆
Temps : 20 min
Question 1)
Déterminer un ordre de grandeur d'un diamètre angulaire (étoile de type solaire à 1.3 pc, comme l'étoile voisine 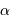 du Centaure) ou planétaire (Jupiter).
du Centaure) ou planétaire (Jupiter).
Traduire le diamètre solaire en UA peut-être utile.
Question 2)
Pourquoi observe-t-on à l'oeil nu le phénomène de scintillation sur une étoile et non sur une planète ?
Le seeing dans le visible est de l'ordre de 1"
 Seeing et flux collecté
Seeing et flux collecté
Difficulté : ☆☆
Temps : 40 min
Un spectromètre est nourri par une fibre qui recueille un champ de 1" sur le ciel. On s'intéresse au flux recueilli par la fibre, et on propose un modèle pour l'estimer.
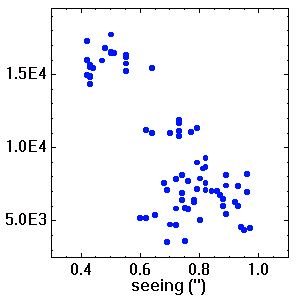
Flux (en photoélectrons) recueilli par la fibre, en fonction du seeing (instrument HARPS à l'ESO).
Crédit :
ASM
Ce modèle suppose que, le seeing valant 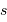 , le flux stellaire se répartit autour de l'image géométrique selon la distribution radiale :
, le flux stellaire se répartit autour de l'image géométrique selon la distribution radiale :
![\phi (r) = \phi_0 \exp\left[-{r^2\over \alpha s^2}\right]](../pages_oa/equations_seeing/equation29.png)
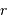 mesure l'écart angulaire à l'image géométrique ;
mesure l'écart angulaire à l'image géométrique ; 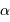 est un facteur sans dimension proche de l'unité.
est un facteur sans dimension proche de l'unité.
Question 1)
Déterminer le flux total 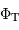 et calculer le flux reçu par une fibre qui sélectionne un rayon
et calculer le flux reçu par une fibre qui sélectionne un rayon 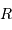 .
.
[3 points]



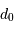 .
A cause de la turbulence, un grand télescope (de diamètre
.
A cause de la turbulence, un grand télescope (de diamètre 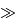
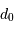 )
a une résolution angulaire identique à celle d'un télescope de diamètre
)
a une résolution angulaire identique à celle d'un télescope de diamètre 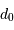 qui ne serait pas affecté par la turbulence. A la longueur d'onde
qui ne serait pas affecté par la turbulence. A la longueur d'onde 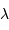 , le seeing vaut :
, le seeing vaut :
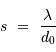
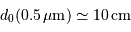 ,
et un très bon seeing par
,
et un très bon seeing par
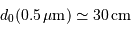 .
Le paramètre
.
Le paramètre 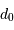 est fortement chromatique :
est fortement chromatique :
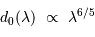
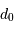 dans l'infrarouge conduit à une dégradation de l'image moindre que dans le visible.
dans l'infrarouge conduit à une dégradation de l'image moindre que dans le visible.
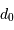 est
est 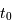 tel que :
tel que :
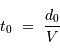
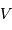 est la vitesse caractéristique du vent.
Une application numérique dans un cas moyen
est la vitesse caractéristique du vent.
Une application numérique dans un cas moyen 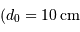 ,
, 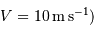 conduit à
conduit à 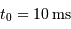 .
Le traitement de la turbulence par optique adaptative va devoir être mené plus rapidement que cette échelle de temps.
.
Le traitement de la turbulence par optique adaptative va devoir être mené plus rapidement que cette échelle de temps.




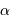 du Centaure) ou planétaire (Jupiter).
du Centaure) ou planétaire (Jupiter).
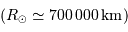 est une étoile moyenne.
Quant à Jupiter :
est une étoile moyenne.
Quant à Jupiter : 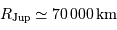 et
et
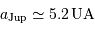 .
.

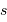 , le flux stellaire se répartit autour de l'image géométrique selon la distribution radiale :
, le flux stellaire se répartit autour de l'image géométrique selon la distribution radiale :
![\phi (r) = \phi_0 \exp\left[-{r^2\over \alpha s^2}\right]](../pages_oa/equations_seeing/equation29.png)
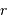 mesure l'écart angulaire à l'image géométrique ;
mesure l'écart angulaire à l'image géométrique ; 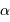 est un facteur sans dimension proche de l'unité.
est un facteur sans dimension proche de l'unité.
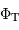 et calculer le flux reçu par une fibre qui sélectionne un rayon
et calculer le flux reçu par une fibre qui sélectionne un rayon 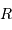 .
.
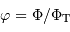 . Représenter
. Représenter 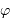 en fonction du seeing (en considérant
en fonction du seeing (en considérant 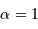 ). Expliquer le comportement pour un bon seeing ou un mauvais seeing (avec respectivement
). Expliquer le comportement pour un bon seeing ou un mauvais seeing (avec respectivement 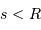 ou
ou 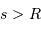 ).
).
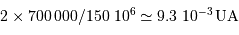 .
A 1.3 pc, le diamètre angulaire vaut donc
.
A 1.3 pc, le diamètre angulaire vaut donc 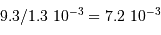 ".
".
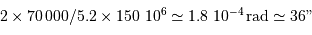 .
.
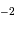 " et 40". Ces valeurs sont à comparer au seeing de l'ordre de 1".
" et 40". Ces valeurs sont à comparer au seeing de l'ordre de 1".
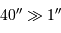 , pas de scintillation dans le cas planétaire.
, pas de scintillation dans le cas planétaire.