Dans ce chapitre, nous allons sortir un peu du cadre de l'optique géométrique pour aborder rapidement les problèmes de diffraction et définir la résolution d'un télescope. Nous verrons quelles solutions existent pour améliorer celle-ci en l'absence et en présence de turbulence atmosphérique.
Ce dernier chapitre ne se veut absolument pas un cours d'optique ondulatoire, ni même une présentation détaillée des phénomènes de diffraction et d'interférences, mais juste une introduction à ces phénomènes ou une mise en bouche. Les plus curieux pourront approfondir le sujet en lisant la suite dans le cours Fenêtre sur l'Univers.
 Prérequis
Prérequis
- Optique géométrique
- Rayon lumineux
- Lentilles et miroirs
- Lunettes et télescopes
- Notions sur la nature de la lumière
Rébus

Crédit :
B. Mollier
 Faisceau parallèle et système afocal
Faisceau parallèle et système afocal
Considérons un faisceau de lumière collimaté, c'est-à-dire un faisceau parallèle, arrivant sur un système afocal (une lunette astronomique par exemple). Pour simplifier notre étude, nous supposerons que les deux lentilles ont la même focale. (Quel grossissement a cette lentille ?).
Après la première lentille, la lumière converge au foyer principal image, puis diverge pour traverser la seconde lentille d'où elle ressort en faisceau parallèle, de même taille qu'en entrée.
Système afocal
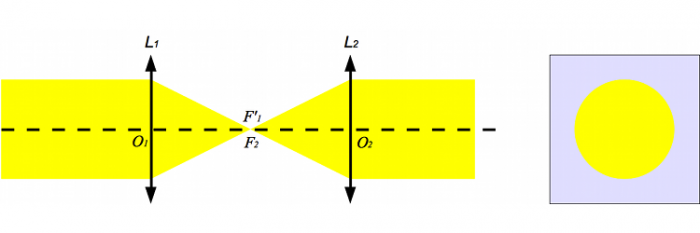
On injecte un faisceau de lumière parallèle dans un système afocal de grossissement 1. À droite, ce qu'on voit projeté sur un écran.
Crédit :
ASM/B. Mollier
 Image d'une plume
Image d'une plume
Plaçons maintenant une plume dans le faisceau incident. Encore pour des raisons de simplicité, on la placera au foyer principal objet de la première lentille.
Recherchons la position de son image. Une petite construction nous la donne assez vite.
Image d'une plume
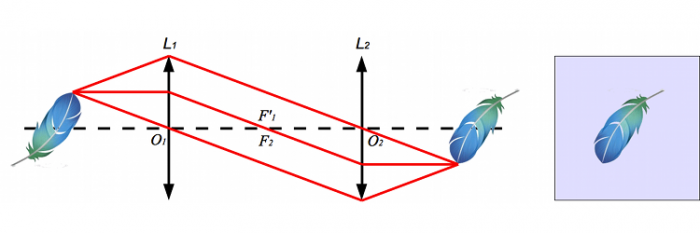
Image d'une plume à travers le système afocal.
Crédit :
ASM/B. Mollier
 Attention !
Attention !
Les rayons lumineux utilisés pour tracer son image sont uniquement des traits de construction, ils ne sont en rien ici physiques. La plume étant éclairée par l'arrière par un faisceau parallèle, seuls ces rayons ressortent effectivement de la lunette. L'image de la plume ne sera que son ombre se dessinant dans le faisceau.
L'ombre de la plume
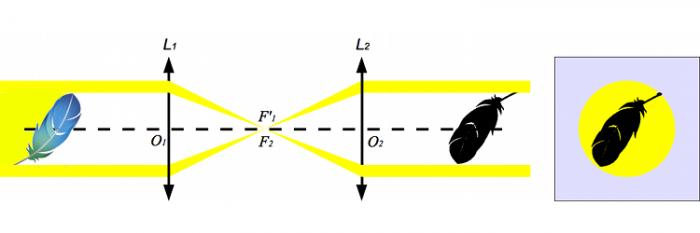
La plume projette son ombre sur l'écran.
Crédit :
ASM/B. Mollier
 Un pastille au foyer des deux lentilles
Un pastille au foyer des deux lentilles
Plaçons une petite pastille au foyer commun des deux lentilles de manière à intercepter le faisceau lumineux. Totalement bloqué, aucune lumière ne ressort de la lentille. L'ombre de notre plume disparaît. Vrai ? Vérifions en plaçant un écran.
Une pastille au foyer
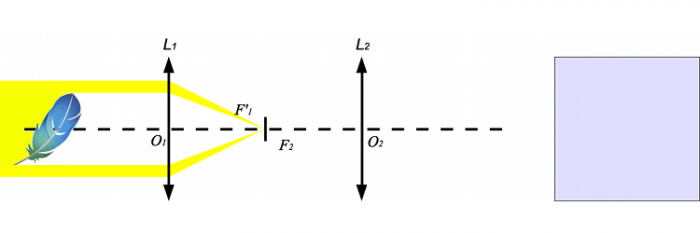
On place une pastille aux foyers des lentilles, de façon à stopper le faisceau. Nous devrions donc ne plus rien voir sur l'écran.
Crédit :
ASM/B. Mollier
 Une image !
Une image !
Contre toute attente, on observe quelque chose en sortie. Ce sont les contours de la plume ! Mais d'où vient cette lumière ?
Strioscopie
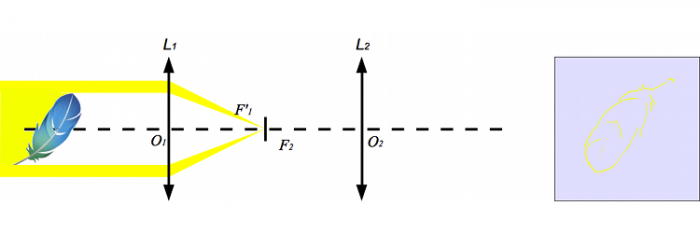
Aussi étonnant que cela paraisse, on obtient bien une image à l'écran. Les contours de la plume se dessinent sur celui-ci. Cette expérience s'appelle strioscopie.
Crédit :
ASM/B. Mollier
Si on reste dans le cadre de l'optique géométrique, les rayons lumineux sont censés se propager en ligne droite. Ils ne sont pas déviés au passage de la plume, celle-ci imprimant son ombre dans le faisceau. Ils sont stoppés par la pastille.
Si des rayons ressortent de la lunette, c'est qu'ils sont passés à côté de la pastille. L'hypothèse des trajectoires rectilignes des rayons lumineux ne tient pas. Nous venons de mettre en évidence une limite de l'optique géométrique.
 Mise en évidence de la diffraction
Mise en évidence de la diffraction
Ce n'est pas la première fois que nous sommes confrontés à la diffraction. Souvenez vous du chapitre 1 lorsque l'on cherchait à isoler un rayon lumineux.
Qu'avions-nous vu ? En réduisant progressivement la taille du diaphragme, le diamètre du faisceau diminuait, puis, mystérieusement recommençait à croître. En dessous d'un certain diamètre du diaphragme, le faisceau diverge. Ce phénomène est appelé diffraction.
Isoler un rayon lumineux ?

Il est impossible d'isoler un rayon lumineux à cause de la diffraction.
Crédit :
ASM/B. Mollier
 Apparition de la diffraction
Apparition de la diffraction
La diffraction est cette tendance naturelle qu'a la lumière à diverger dès qu'on cherche à la confiner (au passage d'un diaphragme par exemple).
La diffraction est due à la nature ondulatoire de la lumière. Si on reprend le modèle d'ondelette de Huygens, on parvient à sentir le phénomène. Lorsque l'ouverture est grande, l'onde plane incidente ressort quasiment plane. Le phénomène de diffraction est négligeable. Par contre, si l'ouverture est faible, l'onde transmise est presque sphérique.
Ondelettes de Huygens
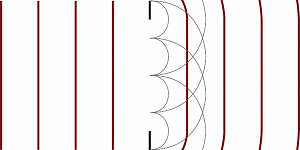

Si l'ouverture est large devant la longueur d'onde, l'onde sortante est plane. Si l'ouverture est petite, l'onde sortante est sphérique. Il y a diffraction.
Crédit :
ASL/B. Mollier
Plus l'ouverture est petite, plus la diffraction sera importante. En fait, l'angle de divergence du faisceau est inversement proportionnel à la taille de l'ouverture. Notez bien ce résultat, il est important en astronomie.
La diffraction se manifeste lorsque la lumière croise un objet dont les dimensions sont comparables à sa longueur d'onde (plus généralement des variations d'opacité sur des échelles de l'ordre de la longueur d'onde, comme des bords francs par exemple).
 Figure de diffraction
Figure de diffraction
Voici quelques exemples de figures de diffraction. On les obtient en cherchant à faire l'image d'une source ponctuelle située à l'infini (une étoile) avec une lentille devant laquelle on place un diaphragme.
Exemples de figures de diffraction

À gauche, la figure de diffraction donnée par une ouverture carrée. À droite, celle donnée par une ouverture circulaire. Cette dernière s'appelle "tache d'Airy".
Crédit :
ASM/B. Mollier
On voit que le modèle de Huygens permet uniquement de sentir le phénomène, mais pas de l'expliquer totalement. En effet, il n'explique pas la présence d'anneau autour de la tache d'Airy.
Phénomène de diffraction

À gauche, une photo d'un village à la tombée de la nuit. À droite, la même photo, mais on a refermé le rideau. On voit alors apparaître des taches de diffraction au niveau des réverbères, car les mailles du rideau sont très petites. On reconnaît la figure de diffraction caractéristique d'une ouverture carrée.
Crédit :
D. Pickel (avec son aimable autorisation)
 En optique géométrique... ça ne marche pas.
En optique géométrique... ça ne marche pas.
En optique géométrique, les rayons se propagent en ligne droite. Ils ne changent pas de direction au passage de la plume. Ils sont donc toujours parallèles à l'axe optique lorsqu'ils atteignent l'objectif. Ils passent donc tous par le foyer et sont, en théorie, arrêtés par la pastille. Aucune image n'est visible en sortie. Et pourtant...
En optique géométrique...
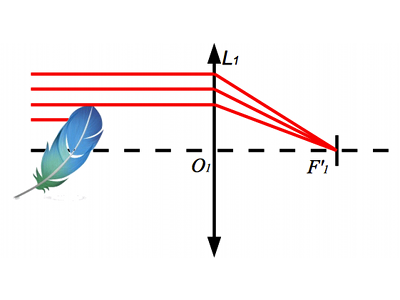
En optique géométrique, tous les rayons étant parallèles à l'axe optique, ils se croisent au foyer image et sont stoppés par la pastille.
Crédit :
ASM/B. Mollier
 En optique ondulatoire, ça fonctionne !
En optique ondulatoire, ça fonctionne !
Il faut donc abandonner l'optique géométrique.
Au contact de la plume, la lumière rencontre des bords francs et des fibres de petites dimensions. La diffraction fait diverger une partie des rayons. Ces derniers ne sont plus parallèles à l'axe optique. Ils ne passent donc plus par le foyer de l'objectif. Ils contournent alors la pastille, et ressortent imprimer l'écran.
En optique ondulatoire...
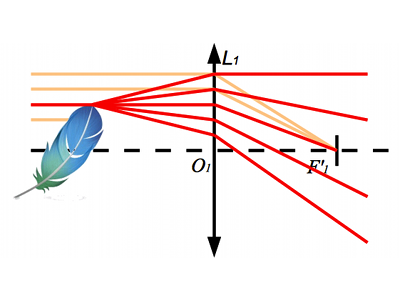
Les rayons frôlant les bords de la plume (et seulement eux) sont diffractés, et parviennent à contourner la pastille. Les contours de la plume apparaissent sur l'écran.
Crédit :
ASM/B. Mollier
La diffraction n'apparaissant qu'aux bords de la plume (ou de n'importe quel objet), seuls les rayons issus des bords sont déviés. Ils sont les seuls à contourner la pastille et à imprimer l'écran. On voit les bords de la plume !
 La diffraction existe toujours !
La diffraction existe toujours !
Et au télescope ? La diffraction existe-t-elle ? Non, me direz vous. La pupille d'entrée d'un télescope est grande. Bien plus grande que la longueur d'onde de la lumière. Vous auriez en partie raison.
Mais en fait, la diffraction se manifeste tout le temps. Elle est certes d'autant plus visible que les ouvertures sont petites, mais elle est quand même présente aux grandes ouvertures.
 L'image d'une étoile
L'image d'une étoile
Autrement dit, l'image d'une étoile à travers un télescope, ne sera jamais ponctuelle. Ce sera une petite tache, d'autant plus grande que le diamètre du télescope est petit.
Image d'une étoile à travers un télescope
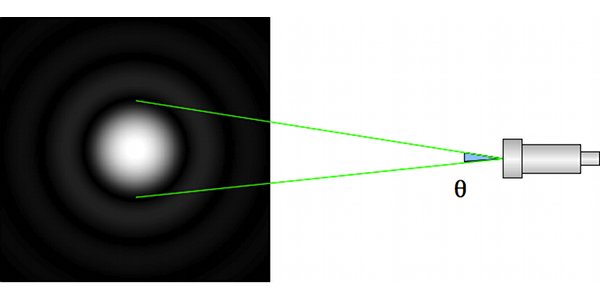
À cause de la diffraction, l'image d'une étoile n'est pas ponctuelle. C'est une tache entourée d'anneaux. Cette figure est appelée tache d'Airy. La taille de la tache et des anneaux est d'autant plus grande que le diamètre du télescope est petit.
Crédit :
ASM/B. Mollier
On montre que le diamètre angulaire de la tache image de l'étoile est inversement proportionnel au diamètre du télescope ou de la lunette :
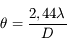
 Commentaires
Commentaires
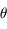 est un angle apparent.
est un angle apparent.- La taille de la tache est inversement proportionnelle au diamètre
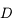 du télescope.
du télescope. - Elle est proportionnelle à la longueur d'onde.
- Plus la longueur d'onde est grande, plus la diffraction se manifeste facilement.
 Tout n'est pas visible au télescope
Tout n'est pas visible au télescope
Au lieu de voir des étoiles ponctuelles à travers un télescope, on voit des taches. La diffraction brouille les images astronomiques. Pour un diamètre donné d'un télescope, tous les détails ne seront pas visibles. Si les plus gros pourront être vus, les plus fins, seront flous, et donc non visibles à l'oeil ou à l'appareil photo.
Plus le diamètre sera grand, plus fins seront les détails visibles. On voit ici le deuxième intérêt d'avoir un grand télescope, en plus de la quantité de lumière collectée.
Résolution d'une étoile double

Plus le diamètre du télescope augmente, plus la tache d'Airy diminue. Au dessus d'un certain diamètre, l'étoile apparaît double !
Crédit :
ASM/B. Mollier
 Résoudre une étoile double
Résoudre une étoile double
On cherche à observer une étoile double. Une étoile double est en fait un couple de deux étoiles. Elles peuvent être liées gravitationnellement. Elles tournent alors l'une autour de l'autre, et sont donc proches physiquement. C'est une étoile binaire. Plus de la moitié des étoiles de la galaxie vivent ainsi en couple. Albireo est un système binaire.
Cela peut aussi être uniquement un effet de perspective. Elles nous apparaissent proches l'une de l'autre, mais en fait, l'une est beaucoup plus proche de nous que la seconde. C'est un hasard si elles sont alignées. Alcor et Mizar, dans la constellation de la grande Ourse, sont un exemple d'étoiles binaires visuelles. Elles sont en fait séparées de 3 années-lumière !
Si ces étoiles sont très écartées dans le plan du ciel, pas de souci, on verra deux taches. Mais si elles sont très proches, leur tache commence à se mêler et on ne parvient plus à les distinguer l'une de l'autre.
Résolution d'une étoile double

Crédit :
ASM/B. Mollier
Ce n'est pas la peine d'augmenter le grossissement en changeant d'oculaire ! Il n'y est pour rien. La diffraction ne dépend que de la taille du télescope. Il faut donc augmenter son diamètre pour augmenter sa résolution.
 Résolution d'un télescope
Résolution d'un télescope
La résolution d'un télescope est sa capacité à distinguer de fins détails.
On définit un critère quantitatif pour calculer la résolution d'un télescope. Il s'agit du critère de Rayleigh.
L'oeil parvient à distinguer une binaire à partir du moment où le centre de la première tache est au niveau du bord de la seconde.
Critère de Rayleigh

On distingue les deux étoiles lorsque le premier anneau sombre (surligné en rouge) se superpose au centre de la seconde tache d'Airy (croix verte).
Crédit :
ASM/B. Mollier
On distingue donc une binaire à partir du moment où l'écartement 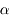 entre les deux étoiles est supérieur au rayon
entre les deux étoiles est supérieur au rayon 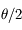 de la tache de diffraction.
de la tache de diffraction.
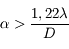
La résolution du télescope est donnée par la valeur limite 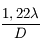 . Il est impossible de distinguer des détails plus petits que cet angle.
. Il est impossible de distinguer des détails plus petits que cet angle.
Auteur: B. Mollier
 Résolution d'un télescope
Résolution d'un télescope
L'étoile NX de la constellation des voiles (hémisphère sud) est en fait une étoile double. La séparation angulaire entre les deux composantes est de 0,7 seconde d'angle.
Constellation des voiles
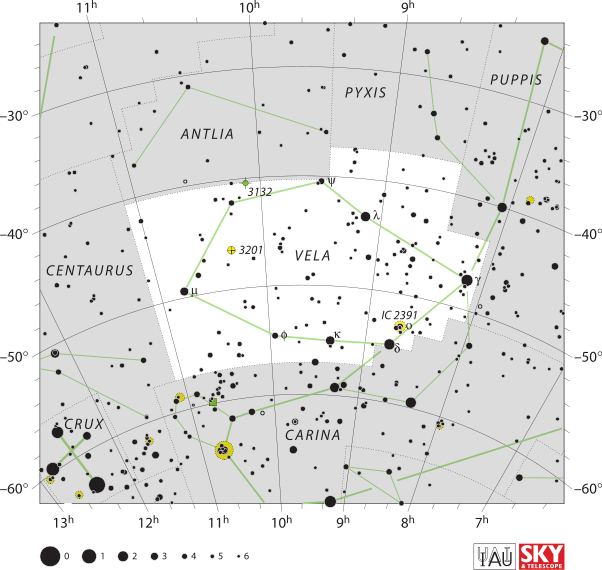
Crédit :
UAI/Sky & Telescope
nx Vel

L'étoile nx Vel.
Crédit :
Aladin
Question 1)
Quelle est la taille minimale du miroir primaire nécessaire pour pourvoir résoudre cette étoile double ? On l'observera dans le visible.
On vient de voir que la résolution d'un instrument est limitée par son diamètre. Changer de grossissement ne change pas la résolution. Que faire pour l'accroître ?
 Changer de longueur d'onde
Changer de longueur d'onde
On peut changer de longueur d'onde. En diminuant la longueur d'onde, on augmente la résolution.
Cependant, ça ne convient pas forcément à tous les cas. En effet, les techniques d'acquisition d'image ne sont pas les mêmes en radio, en infrarouge, dans le visible ou dans l'UV.
On n'observe pas non plus les mêmes objets ou phénomènes en fonction de la longueur d'onde. Aux grandes longueurs d'onde, on observe les objets froids et les phénomènes peu énergétiques. Aux petites longueurs d'onde, on observe les objets chauds et les phénomènes énergétiques.
 Augmenter le diamètre
Augmenter le diamètre
Que nous reste-t-il ? Augmenter le diamètre du télescope. Les plus grands télescopes actuels mesurent 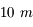 de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
Pour pouvoir voir des exoplanètes, il faut de plus grands diamètres encore. L'Europe projette de construire au Chili un télescope de 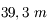 de diamètre.
de diamètre.
Les grands télescopes

L'European Extremely Large Telescope (E-ELT), avec un miroir large de
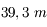
à côté des VLTs, parmi les plus grands télescopes actuels (
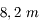
).
Crédit :
ESO
Pour augmenter encore la résolution, il faudrait augmenter encore la taille des miroirs des télescopes. Mais à l'heure actuelle, des miroirs de 100 et a fortiori 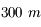 ne sont pas envisageables. Comment faire ? La réponse est surprenante.
ne sont pas envisageables. Comment faire ? La réponse est surprenante.
Il suffit d'utiliser deux télescopes espacés de 100, 200 ou 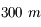 , et de mélanger (on dit faire interférer) la lumière qui en est issue ! Incroyable, mais 2 petits télescopes distants de
, et de mélanger (on dit faire interférer) la lumière qui en est issue ! Incroyable, mais 2 petits télescopes distants de 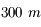 ont le même pouvoir de résolution qu'un unique télescope de
ont le même pouvoir de résolution qu'un unique télescope de 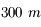 !
!
Deux petits valent mieux qu'un grand
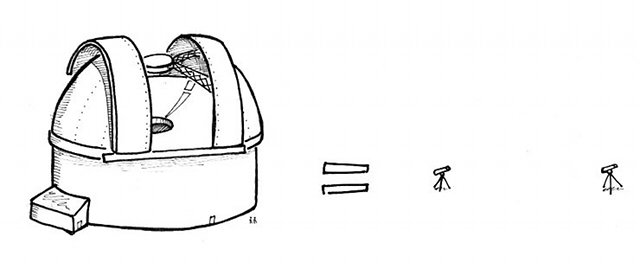
La résolution de deux télescopes espacés de
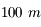
est la même qu'un unique télescope de
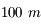
de diamètre.
Crédit :
B. Mollier
Comment ça marche ?
 Quand deux houles se croisent
Quand deux houles se croisent
La lumière peut être vue comme une onde au même titre que la houle. Si je pose une bouée sur l'eau, elle oscille avec la houle.
Houle d'ouest
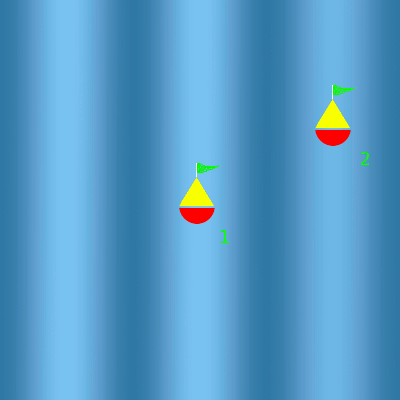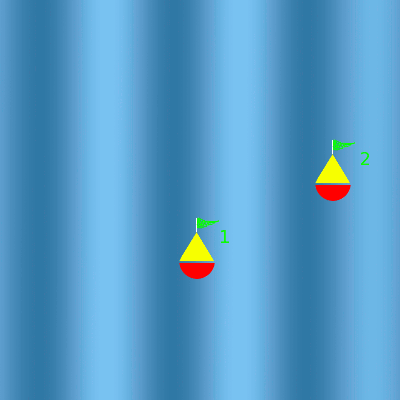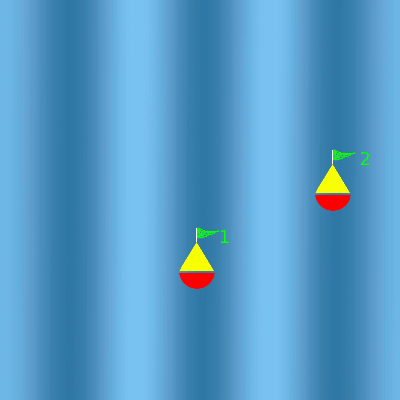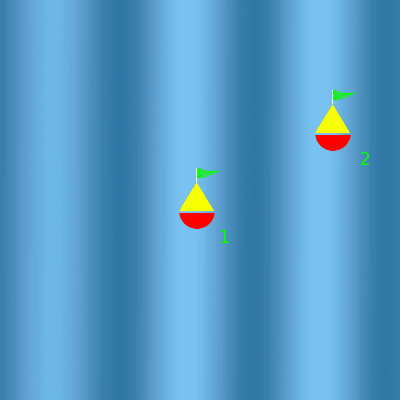
La houle fait osciller les deux bouées. Comme elles sont espacées d'est en ouest d'une longueur d'onde, elles oscillent en phase.
Crédit :
ASM/B. Mollier
Si deux houles se croisent, à certains endroits les vaguent s'additionnent, et l'amplitude d'oscillation de la bouée augmente. Les crêtes des deux vagues arrivent en même temps, ainsi que les deux creux. On parle d'interférences constructives.
Houle du nord
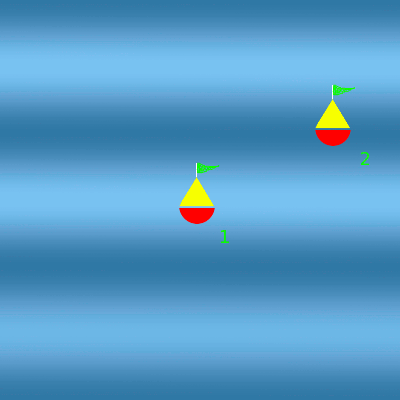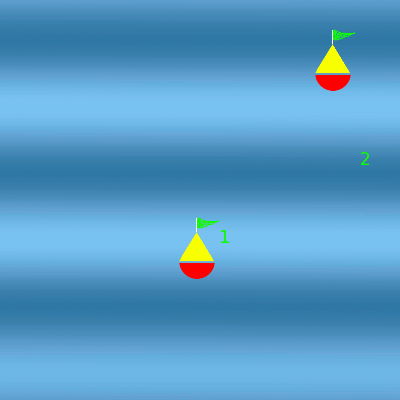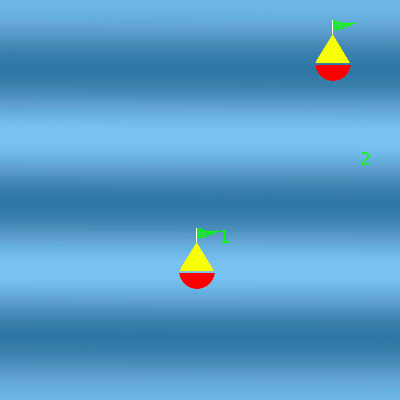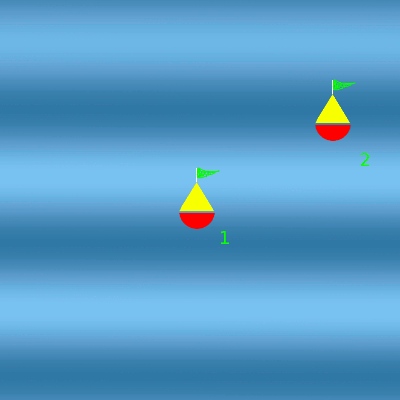
La houle fait osciller les deux bouées. Comme elles sont espacées du nord au sud d'une demi-longueur d'onde, elles oscillent en opposition de phase.
Crédit :
ASM/B. Mollier
À d'autres endroits, au contraire, à une crête de la première houle correspond un creux de la seconde. Les vagues s'annulent. La bouée n'oscille pas à ces endroits. On parle d'interférences destructives.
Les deux houles se croisent
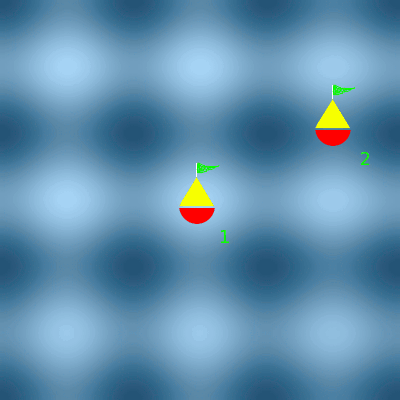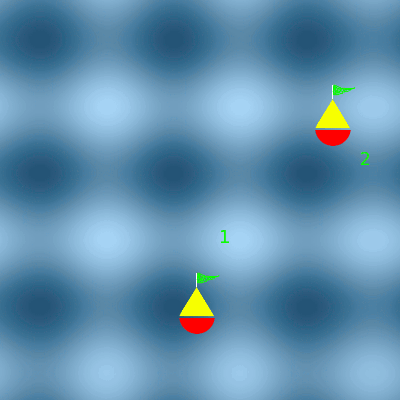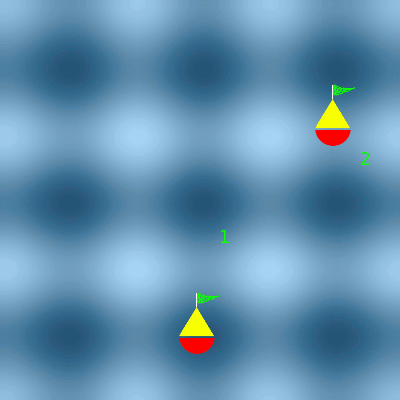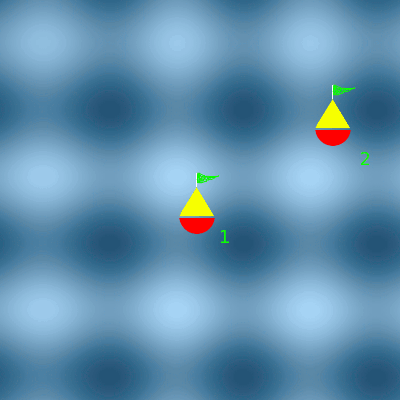
Au niveau de la bouée 1, les houles sont en phase. Les amplitudes s'additionnent. La bouée 1 oscille deux fois plus. Au niveau de la bouée 2, les houles sont en opposition de phase. Les amplitudes s'annulent. La bouée 2 n'oscille plus.
Crédit :
ASM/B. Mollier
 Interférences lumineuses
Interférences lumineuses
Si, par un jeu astucieux de miroirs, et/ou de fibres optiques, on arrive à faire parvenir au même endroit la lumière issue des deux télescopes, on créera aussi des interférences.
Interférences lumineuses

Si on fait passer une onde plane (une "houle") à travers deux trous (ou deux télescopes), on obtient des interférences en sortie.
Crédit :
ASM/B. Mollier
Sur l'image issue des deux télescopes, on verra des zones claires, où les lumières s'additionnent. On parle de franges d'interférence claires. Ce sont les zones où les interférences sont constructives.
On verra également des zones sombres, sans lumière, où les interférences sont destructives. On appelle ces zones des franges sombres.
Interférences lumineuses

Certaines zones sont alternativement blanches et noires. Les "vagues" ont une forte amplitude, les interférences sont constructives. D'autres sont tout le temps grises. Les interférences y sont destructives.
Crédit :
ASM/B. Mollier
 Une image à un seul télescope
Une image à un seul télescope
Comment exploiter ces interférences ? Revenons d'abord au cas à un seul télescope pour bien comprendre ce qui se passe. Si la diffraction n'existait pas, on verrait notre étoile comme un tout petit disque (en jaune sur les images). Or, la diffraction est là, et on ne peut pas faire sans. À la place, on obtient une tache, plus grosse que le petit disque.
Si on augmente la taille du télescope, la taille de la tache diminue. Si le télescope est suffisamment grand, la tache d'Airy est alors plus petite que l'image théorique (donnée par l'optique géométrique) de l'étoile. Notre étoile est résolue !
Augmenter la résolution

Pour accroître la résolution, on augmente le diamètre du télescope jusqu'à ce que la tache de diffraction devienne plus petite que l'image de l'étoile donnée par l'optique géométrique.
Crédit :
B. Mollier
 Principe de l'interférométrie
Principe de l'interférométrie
Passons à deux télescopes. L'image ressemble alors à une grosse tache avec des franges claires et des franges sombres. L'image théorique du disque est perdue au milieu de la frange centrale.
Comment augmenter encore la résolution ?

Pour accroître la résolution, on écarte les télescopes jusqu'à ce que la largeur de la frange centrale devienne plus petite que l'image de l'étoile donnée par l'optique géométrique.
Crédit :
B. Mollier
Si on écarte les télescopes, l'épaisseur des franges diminue. Il y a de plus en plus de franges, et elles sont de plus en plus fines.
Et au bout d'un moment, l'épaisseur de la frange centrale devient plus petite que la taille du disque. L'image de l'étoile déborde de la frange centrale, et bave sur les franges sombres autour. Il y a de la lumière qui apparaît sur ces franges sombres.
Plus on augmente l'écartement des télescopes, plus on diminue l'épaisseur des franges, plus l'étoile déborde sur les côtés, plus il y a de lumière dans les franges sombres.
Quand les franges disparaissent, l'étoile est résolue ! Il existe une relation simple pour trouver le diamètre angulaire de l'étoile en fonction de l'écartement 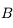 (on parle de base) des télescopes :
(on parle de base) des télescopes :
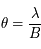
Et ça marche ?
 Les premières expériences
Les premières expériences
Oui. La première expérience d'interférométrie stellaire a été réalisée au début du vingtième siècle par Michelson. À l'entrée du télescope de 100 pouces du mont Wilson (photos), il a fixé une poutre sur laquelle étaient installés deux périscopes d'écartement variable.
Le télescope de 100 pouces du Mont Wilson

Le télescope de 100 pouces (Mont Wilson) au sommet duquel Michelson avait fixé une poutre et deux périscopes. Il effectua avec les premières mesures de diamètre stellaire. C'est aussi sur ce télescope que Hubble observa la fuite des galaxies.
Crédit :
B. Mollier
Interféromètre stellaire de Michelson

L'interféromètre que Michelson installa au sommet du télescope de 100 pouces du Mont Wilson. À ne pas confondre avec l'interféromètre qu'il mit au point avec Morley pour mesurer la vitesse de la lumière.
Crédit :
B. Mollier
Il obtenait en sortie de télescope une tache d'Airy barrée de franges d'interférence. En écartant les miroirs sur la poutre, il faisait varier la base de l'interféromètre jusqu'à disparition des franges. Il en déduisit ainsi le diamètre apparent de Bételgeuse et d'une dizaine d'autres étoiles.
La technique tomba cependant dans l'oubli jusqu'aux années 1970, où l'astronome français Antoine Labeyrie réalisa le premier interféromètre à deux télescopes. Sur le plateau de Calern, ainsi qu'à l'observatoire de Meudon, il parvint à obtenir les premières franges d'interférences en utilisant deux petits télescopes. La principale difficulté étant que la lumière issue des deux télescopes doit avoir parcouru exactement la même distance depuis l'étoile.
 Les futurs projets
Les futurs projets
L'avenir est riche en projets. Les plus "simples", sont des interféromètres classiques où on augmenterait la taille des bases. L'interféromètre NPOI de la Navy américaine possédera des bases de 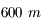 mais avec des télescopes de
mais avec des télescopes de 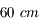 seulement.
seulement.
Plus ambitieux, les projets d'hypertélescopes du même Antoine Labeyrie. Il s'agira de tapisser une cuvette naturelle (un cratère, une vallée...) de miroirs, de suspendre le recombineur à une nacelle au dessus pour obtenir un télescope virtuel de quelques kilomètres de diamètre.
Enfin, des projets d'interféromètres spatiaux sont à l'étude. Ils permettraient de s'affranchir de l'atmosphère, et d'atteindre de très grandes bases (de quelques centaines de mètres à ... jusqu'où on pourra aller).
Un télescope de 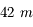 pour voir des exoplanètes, c'est bien joli, mais sa résolution n'est que théorique. On a oublié un détail. L'atmosphère !
pour voir des exoplanètes, c'est bien joli, mais sa résolution n'est que théorique. On a oublié un détail. L'atmosphère !
Effet de la turbulence sur la qualité des images

La galaxie NGC 7469, observée avec et sans optique adaptative (PUEO, CFHT).
Crédit :
CFHT
La turbulence atmosphérique
L'atmosphère n'est pas homogène. Elle est composée de multiples bulles de température et d'humidité différentes. Leurs indices optiques sont donc différents. Les rayons lumineux issus d'une étoile subissent des réfractions différentes et aléatoires en fonction de la zone d'atmosphère traversée.
À cause de l'atmosphère, les rayons lumineux n'arrivent plus parallèles entre eux au niveau du sol, mais avec des angles d'incidence aléatoires !
Conséquences sur l'image d'une étoile
En l'absence d'atmosphère, tous les rayons arrivent parallèles entre eux. Si on pointe un télescope vers une étoile, les rayons convergent donc en un seul point : le foyer du télescope.
Mais en présence de turbulence, les rayons ne convergent plus en un point, mais dans une zone, plus ou moins grande en fonction de l'intensité de la turbulence.
Effet de la turbulence atmosphérique
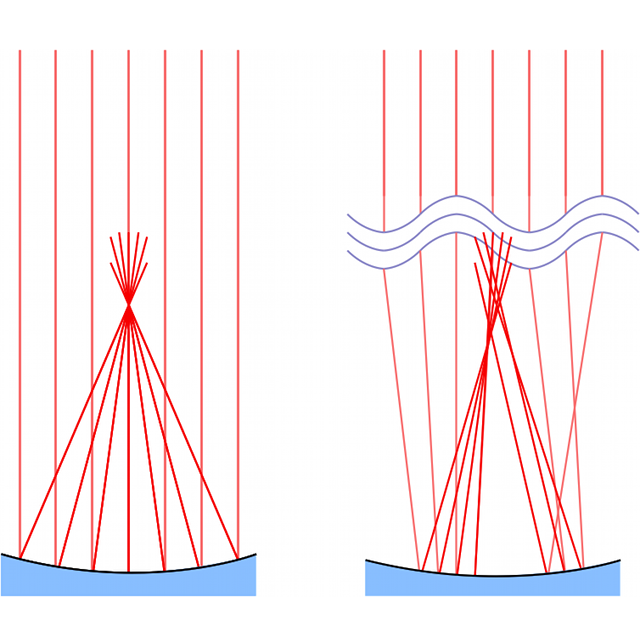
À cause de la turbulence, les rayons ne convergent plus au foyer du télescope.
Crédit :
ASM/B. Mollier
On n'observe plus une jolie petite tache de diffraction, mais une grosse tache granuleuse, variant aléatoirement dans le temps.
 Paramètre de Fried
Paramètre de Fried
La taille de la tache image, en présence de turbulence, est plus grosse que la tache d'Airy. Tout se passe comme si notre télescope avait rétréci et fournissait une tache de diffraction beaucoup plus grosse que prévue.
On définit alors une quantité 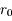 , homogène à un diamètre, appelé paramètre de Fried. Il s'agit du diamètre qu'aurait un télescope qui fournirait, en l'absence de turbulence, une tache d'Airy de même taille que notre télescope en présence de turbulence.
, homogène à un diamètre, appelé paramètre de Fried. Il s'agit du diamètre qu'aurait un télescope qui fournirait, en l'absence de turbulence, une tache d'Airy de même taille que notre télescope en présence de turbulence.
Ce diamètre 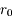 est en général de l'ordre de
est en général de l'ordre de 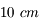 , dans le visible. Dans certains sites de très bonne qualité (dans les déserts, en altitude... bref, là où on construit les nouveaux observatoires) il est plus grand, mais n'excède jamais
, dans le visible. Dans certains sites de très bonne qualité (dans les déserts, en altitude... bref, là où on construit les nouveaux observatoires) il est plus grand, mais n'excède jamais 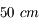 . Dans l'infrarouge, il est plus grand, de l'ordre de
. Dans l'infrarouge, il est plus grand, de l'ordre de 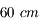 .
.
Pour résumé, en présence de turbulence, un grand télescope de 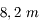 possède la même résolution qu'un télescope de...
possède la même résolution qu'un télescope de... 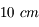 ! Aïe. À quoi bon construire de grands télescopes ?
! Aïe. À quoi bon construire de grands télescopes ?
Heureusement, il existe une technique pour corriger cette turbulence, et rendre la vue perçante à ces gros télescopes.
Pour corriger la turbulence, on utilise un système nommé optique adaptative. Il s'agit d'un miroir déformable qui compense la turbulence atmosphérique.
Comment ça marche ?
Le problème est, qu'avec la turbulence, les rayons n'arrivent plus parallèles entre eux, se réfléchissent avec des tas d'angles différents, et ne convergent plus en un point.
L'astuce consiste à utiliser un miroir déformable, qui change localement l'inclinaison de la surface réfléchissante. L'angle d'incidence du rayon lumineux est modifié de façon à ce que le rayon réfléchit passe par le foyer du télescope.
Principe de fonctionnement de l'optique adaptative
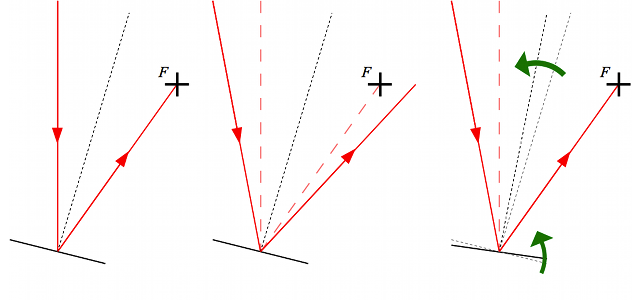
En l'absence de turbulence, le rayon incident arrive à la verticale du miroir, et son rayon réfléchi passe par le foyer (à gauche). Mais à cause de la turbulence, l'incidence du rayon change. Le rayon réfléchi ne passe plus par le foyer (au centre). Grâce à l'optique adaptative, on change l'inclinaison du miroir de façon à ce que le rayon réfléchi passe de nouveau par le foyer (à droite).
Crédit :
ASM/B. Mollier
Ce miroir est placé après le miroir primaire (c'est parfois le miroir secondaire). Il doit compenser la turbulence atmosphérique en temps réel ! Il faut donc analyser la déformation de l'image, calculer la correction à apporter et déformer le miroir en quelques fractions de seconde ! Impressionnant ! Mais ça fonctionne.
L'optique adaptative
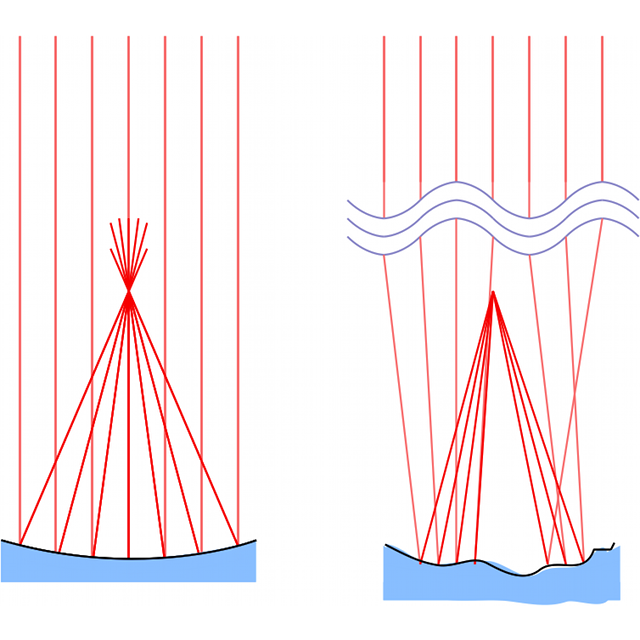
On déforme le miroir de façon à ce que tous les rayons réfléchis passent par le foyer.
Crédit :
ASM/B. Mollier
Ta da !!

Sans optique adaptative (à gauche), l'étoile double n'est pas résolue. Avec l'optique adaptative (à droite), le système d'optique adaptative permet de distinguer les 2 composantes de l'étoile double.
Crédit :
ESO
 La diffraction
La diffraction
Lorsque la taille des obstacles rencontrés par la lumière est comparable à sa longueur d'onde, l'optique géométrique ne s'applique plus. Les rayons ne se propagent plus en ligne droite. C'est la diffraction.
 La tache d'Airy
La tache d'Airy
À cause de la diffraction, l'image d'une étoile n'est pas ponctuelle, mais a la forme d'une tache circulaire, entourée d'anneaux. C'est la tache d'Airy. Sa taille est inversement proportionnelle au diamètre du télescope.
 La résolution d'un télescope
La résolution d'un télescope
La résolution du télescope est sa capacité à distinguer de petits détails. Elle est donnée par la relation :
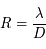
Tout détail plus petit que ce diamètre apparent ne sera pas résolu. La résolution est inversement proportionnelle au diamètre du télescope.
 L'optique adaptative
L'optique adaptative
La turbulence atmosphérique dégrade considérablement la qualité des images en faisant chuter drastiquement la résolution des instruments. Il existe cependant une technique, appelée optique adaptative, qui restaure en grande partie la qualité des images. Son principe repose sur la correction en temps réel de la turbulence, en déformant un miroir pour focaliser tous les rayons lumineux au foyer.
 Prérequis
Prérequis













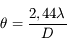
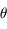 est un angle apparent.
est un angle apparent.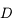 du télescope.
du télescope.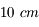 de diamètre, observant dans le visible.
de diamètre, observant dans le visible.
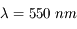 .
.
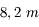 , observant dans la bande
, observant dans la bande 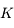 . Sera-t-il possible d'observer Bételgeuse (
. Sera-t-il possible d'observer Bételgeuse (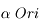 ) ?
) ?

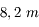 de diamètre.
de diamètre.

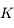 ,
, 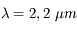 .
.
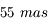



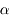 entre les deux étoiles est supérieur au rayon
entre les deux étoiles est supérieur au rayon 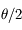 de la tache de diffraction.
de la tache de diffraction.
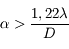
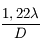 . Il est impossible de distinguer des détails plus petits que cet angle.
. Il est impossible de distinguer des détails plus petits que cet angle.


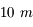 de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
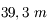 de diamètre.
de diamètre.

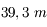 à côté des VLTs, parmi les plus grands télescopes actuels (
à côté des VLTs, parmi les plus grands télescopes actuels (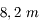 ).
).
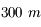 ne sont pas envisageables. Comment faire ? La réponse est surprenante.
ne sont pas envisageables. Comment faire ? La réponse est surprenante.
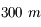 , et de mélanger (on dit faire interférer) la lumière qui en est issue ! Incroyable, mais 2 petits télescopes distants de
, et de mélanger (on dit faire interférer) la lumière qui en est issue ! Incroyable, mais 2 petits télescopes distants de 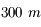 ont le même pouvoir de résolution qu'un unique télescope de
ont le même pouvoir de résolution qu'un unique télescope de 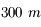 !
!

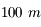 est la même qu'un unique télescope de
est la même qu'un unique télescope de 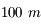 de diamètre.
de diamètre.







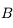 (on parle de base) des télescopes :
(on parle de base) des télescopes :
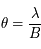


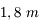 ou 4 télescopes de
ou 4 télescopes de 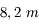 sur des bases allant de
sur des bases allant de 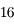 à
à 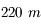 . On peut également citer l'interféromètre CHARA, installé sur le mont Wilson (oui, là où Michelson a construit son premier interféromètre stellaire), qui recombine 6 télescopes de
. On peut également citer l'interféromètre CHARA, installé sur le mont Wilson (oui, là où Michelson a construit son premier interféromètre stellaire), qui recombine 6 télescopes de 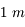 de diamètre sur des bases allant de
de diamètre sur des bases allant de 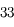 à
à 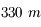 . C'est encore actuellement le plus grand interféromètre visible et infrarouge.
. C'est encore actuellement le plus grand interféromètre visible et infrarouge.

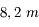 de diamètre ainsi que 4 petits télescopes de
de diamètre ainsi que 4 petits télescopes de 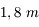 (petite boule au premier plan). Ils constituent actuellement le réseau interférométrique le plus puissant.
(petite boule au premier plan). Ils constituent actuellement le réseau interférométrique le plus puissant.
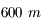 mais avec des télescopes de
mais avec des télescopes de 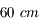 seulement.
seulement.
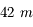 pour voir des exoplanètes, c'est bien joli, mais sa résolution n'est que théorique. On a oublié un détail. L'atmosphère !
pour voir des exoplanètes, c'est bien joli, mais sa résolution n'est que théorique. On a oublié un détail. L'atmosphère !


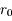 , homogène à un diamètre, appelé paramètre de Fried. Il s'agit du diamètre qu'aurait un télescope qui fournirait, en l'absence de turbulence, une tache d'Airy de même taille que notre télescope en présence de turbulence.
, homogène à un diamètre, appelé paramètre de Fried. Il s'agit du diamètre qu'aurait un télescope qui fournirait, en l'absence de turbulence, une tache d'Airy de même taille que notre télescope en présence de turbulence.
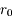 est en général de l'ordre de
est en général de l'ordre de 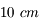 , dans le visible. Dans certains sites de très bonne qualité (dans les déserts, en altitude... bref, là où on construit les nouveaux observatoires) il est plus grand, mais n'excède jamais
, dans le visible. Dans certains sites de très bonne qualité (dans les déserts, en altitude... bref, là où on construit les nouveaux observatoires) il est plus grand, mais n'excède jamais 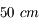 . Dans l'infrarouge, il est plus grand, de l'ordre de
. Dans l'infrarouge, il est plus grand, de l'ordre de 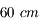 .
.
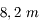 possède la même résolution qu'un télescope de...
possède la même résolution qu'un télescope de... 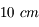 ! Aïe. À quoi bon construire de grands télescopes ?
! Aïe. À quoi bon construire de grands télescopes ?



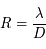
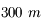 est la même qu'un unique télescope de
est la même qu'un unique télescope de 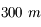 .
.
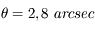
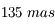 . Le diamètre de la tache d'Airy est plus grand que celui de l'étoile. Bételgeuse n'est donc pas résolue. Du moins, en bande
. Le diamètre de la tache d'Airy est plus grand que celui de l'étoile. Bételgeuse n'est donc pas résolue. Du moins, en bande 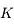 . En visible, elle le serait.
. En visible, elle le serait.
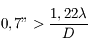
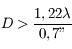
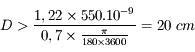
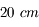 de diamètre.
de diamètre.