 Faisceau parallèle et système afocal
Faisceau parallèle et système afocal
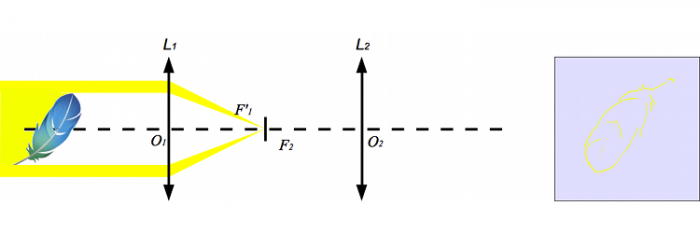
Considérons un faisceau de lumière collimaté, c'est-à-dire un faisceau parallèle, arrivant sur un système afocal (une lunette astronomique par exemple). Pour simplifier notre étude, nous supposerons que les deux lentilles ont la même focale. (Quel grossissement a cette lentille ?).
Après la première lentille, la lumière converge au foyer principal image, puis diverge pour traverser la seconde lentille d'où elle ressort en faisceau parallèle, de même taille qu'en entrée.
Système afocal
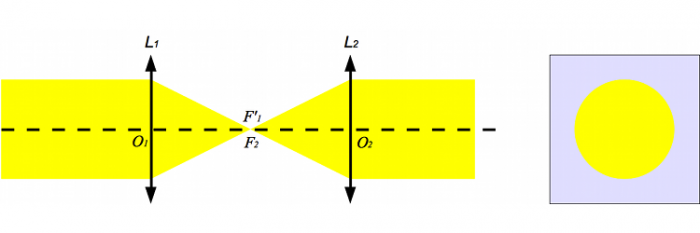
On injecte un faisceau de lumière parallèle dans un système afocal de grossissement 1. À droite, ce qu'on voit projeté sur un écran.
Crédit :
ASM/B. Mollier
 Image d'une plume
Image d'une plume
Plaçons maintenant une plume dans le faisceau incident. Encore pour des raisons de simplicité, on la placera au foyer principal objet de la première lentille.
Recherchons la position de son image. Une petite construction nous la donne assez vite.
Image d'une plume
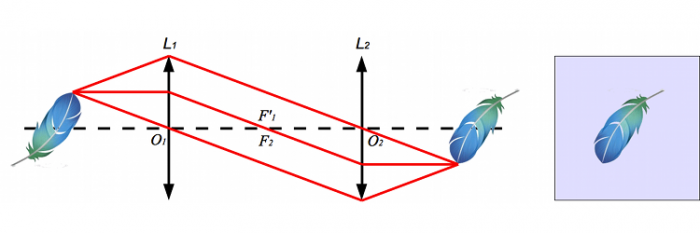
Image d'une plume à travers le système afocal.
Crédit :
ASM/B. Mollier
 Attention !
Attention !
Les rayons lumineux utilisés pour tracer son image sont uniquement des traits de construction, ils ne sont en rien ici physiques. La plume étant éclairée par l'arrière par un faisceau parallèle, seuls ces rayons ressortent effectivement de la lunette. L'image de la plume ne sera que son ombre se dessinant dans le faisceau.
L'ombre de la plume
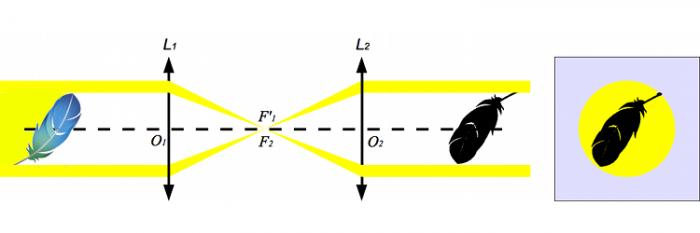
La plume projette son ombre sur l'écran.
Crédit :
ASM/B. Mollier
 Un pastille au foyer des deux lentilles
Un pastille au foyer des deux lentilles
Plaçons une petite pastille au foyer commun des deux lentilles de manière à intercepter le faisceau lumineux. Totalement bloqué, aucune lumière ne ressort de la lentille. L'ombre de notre plume disparaît. Vrai ? Vérifions en plaçant un écran.
Une pastille au foyer
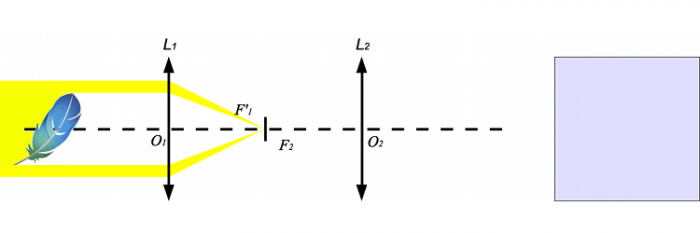
On place une pastille aux foyers des lentilles, de façon à stopper le faisceau. Nous devrions donc ne plus rien voir sur l'écran.
Crédit :
ASM/B. Mollier
 Une image !
Une image !
Contre toute attente, on observe quelque chose en sortie. Ce sont les contours de la plume ! Mais d'où vient cette lumière ?
Strioscopie
Aussi étonnant que cela paraisse, on obtient bien une image à l'écran. Les contours de la plume se dessinent sur celui-ci. Cette expérience s'appelle strioscopie.
Crédit :
ASM/B. Mollier
Si on reste dans le cadre de l'optique géométrique, les rayons lumineux sont censés se propager en ligne droite. Ils ne sont pas déviés au passage de la plume, celle-ci imprimant son ombre dans le faisceau. Ils sont stoppés par la pastille.
Si des rayons ressortent de la lunette, c'est qu'ils sont passés à côté de la pastille. L'hypothèse des trajectoires rectilignes des rayons lumineux ne tient pas. Nous venons de mettre en évidence une limite de l'optique géométrique.
 Mise en évidence de la diffraction
Mise en évidence de la diffraction
Ce n'est pas la première fois que nous sommes confrontés à la diffraction. Souvenez vous du chapitre 1 lorsque l'on cherchait à isoler un rayon lumineux.
Qu'avions-nous vu ? En réduisant progressivement la taille du diaphragme, le diamètre du faisceau diminuait, puis, mystérieusement recommençait à croître. En dessous d'un certain diamètre du diaphragme, le faisceau diverge. Ce phénomène est appelé diffraction.
Isoler un rayon lumineux ?

Il est impossible d'isoler un rayon lumineux à cause de la diffraction.
Crédit :
ASM/B. Mollier
 Apparition de la diffraction
Apparition de la diffraction
La diffraction est cette tendance naturelle qu'a la lumière à diverger dès qu'on cherche à la confiner (au passage d'un diaphragme par exemple).
La diffraction est due à la nature ondulatoire de la lumière. Si on reprend le modèle d'ondelette de Huygens, on parvient à sentir le phénomène. Lorsque l'ouverture est grande, l'onde plane incidente ressort quasiment plane. Le phénomène de diffraction est négligeable. Par contre, si l'ouverture est faible, l'onde transmise est presque sphérique.
Ondelettes de Huygens
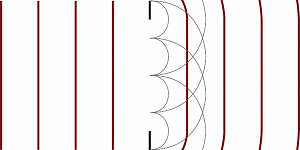

Si l'ouverture est large devant la longueur d'onde, l'onde sortante est plane. Si l'ouverture est petite, l'onde sortante est sphérique. Il y a diffraction.
Crédit :
ASL/B. Mollier
Plus l'ouverture est petite, plus la diffraction sera importante. En fait, l'angle de divergence du faisceau est inversement proportionnel à la taille de l'ouverture. Notez bien ce résultat, il est important en astronomie.
La diffraction se manifeste lorsque la lumière croise un objet dont les dimensions sont comparables à sa longueur d'onde (plus généralement des variations d'opacité sur des échelles de l'ordre de la longueur d'onde, comme des bords francs par exemple).
 Figure de diffraction
Figure de diffraction
Voici quelques exemples de figures de diffraction. On les obtient en cherchant à faire l'image d'une source ponctuelle située à l'infini (une étoile) avec une lentille devant laquelle on place un diaphragme.
Exemples de figures de diffraction

À gauche, la figure de diffraction donnée par une ouverture carrée. À droite, celle donnée par une ouverture circulaire. Cette dernière s'appelle "tache d'Airy".
Crédit :
ASM/B. Mollier
On voit que le modèle de Huygens permet uniquement de sentir le phénomène, mais pas de l'expliquer totalement. En effet, il n'explique pas la présence d'anneau autour de la tache d'Airy.
Phénomène de diffraction

À gauche, une photo d'un village à la tombée de la nuit. À droite, la même photo, mais on a refermé le rideau. On voit alors apparaître des taches de diffraction au niveau des réverbères, car les mailles du rideau sont très petites. On reconnaît la figure de diffraction caractéristique d'une ouverture carrée.
Crédit :
D. Pickel (avec son aimable autorisation)
 En optique géométrique... ça ne marche pas.
En optique géométrique... ça ne marche pas.
En optique géométrique, les rayons se propagent en ligne droite. Ils ne changent pas de direction au passage de la plume. Ils sont donc toujours parallèles à l'axe optique lorsqu'ils atteignent l'objectif. Ils passent donc tous par le foyer et sont, en théorie, arrêtés par la pastille. Aucune image n'est visible en sortie. Et pourtant...
En optique géométrique...
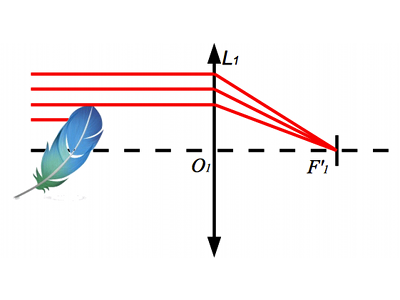
En optique géométrique, tous les rayons étant parallèles à l'axe optique, ils se croisent au foyer image et sont stoppés par la pastille.
Crédit :
ASM/B. Mollier
 En optique ondulatoire, ça fonctionne !
En optique ondulatoire, ça fonctionne !
Il faut donc abandonner l'optique géométrique.
Au contact de la plume, la lumière rencontre des bords francs et des fibres de petites dimensions. La diffraction fait diverger une partie des rayons. Ces derniers ne sont plus parallèles à l'axe optique. Ils ne passent donc plus par le foyer de l'objectif. Ils contournent alors la pastille, et ressortent imprimer l'écran.
En optique ondulatoire...
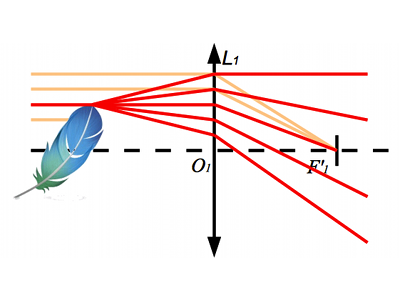
Les rayons frôlant les bords de la plume (et seulement eux) sont diffractés, et parviennent à contourner la pastille. Les contours de la plume apparaissent sur l'écran.
Crédit :
ASM/B. Mollier
La diffraction n'apparaissant qu'aux bords de la plume (ou de n'importe quel objet), seuls les rayons issus des bords sont déviés. Ils sont les seuls à contourner la pastille et à imprimer l'écran. On voit les bords de la plume !
 La diffraction existe toujours !
La diffraction existe toujours !
Et au télescope ? La diffraction existe-t-elle ? Non, me direz vous. La pupille d'entrée d'un télescope est grande. Bien plus grande que la longueur d'onde de la lumière. Vous auriez en partie raison.
Mais en fait, la diffraction se manifeste tout le temps. Elle est certes d'autant plus visible que les ouvertures sont petites, mais elle est quand même présente aux grandes ouvertures.
 L'image d'une étoile
L'image d'une étoile
Autrement dit, l'image d'une étoile à travers un télescope, ne sera jamais ponctuelle. Ce sera une petite tache, d'autant plus grande que le diamètre du télescope est petit.
Image d'une étoile à travers un télescope
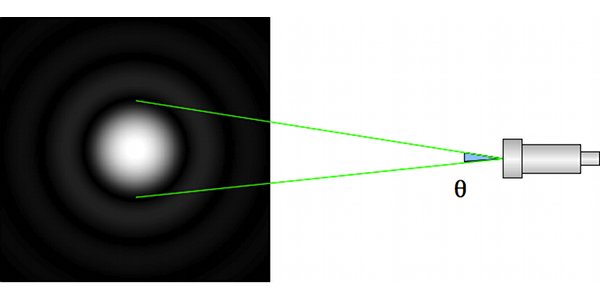
À cause de la diffraction, l'image d'une étoile n'est pas ponctuelle. C'est une tache entourée d'anneaux. Cette figure est appelée tache d'Airy. La taille de la tache et des anneaux est d'autant plus grande que le diamètre du télescope est petit.
Crédit :
ASM/B. Mollier
On montre que le diamètre angulaire de la tache image de l'étoile est inversement proportionnel au diamètre du télescope ou de la lunette :
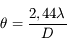
 Commentaires
Commentaires
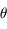 est un angle apparent.
est un angle apparent.- La taille de la tache est inversement proportionnelle au diamètre
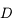 du télescope.
du télescope. - Elle est proportionnelle à la longueur d'onde.
- Plus la longueur d'onde est grande, plus la diffraction se manifeste facilement.
 Tout n'est pas visible au télescope
Tout n'est pas visible au télescope
Au lieu de voir des étoiles ponctuelles à travers un télescope, on voit des taches. La diffraction brouille les images astronomiques. Pour un diamètre donné d'un télescope, tous les détails ne seront pas visibles. Si les plus gros pourront être vus, les plus fins, seront flous, et donc non visibles à l'oeil ou à l'appareil photo.
Plus le diamètre sera grand, plus fins seront les détails visibles. On voit ici le deuxième intérêt d'avoir un grand télescope, en plus de la quantité de lumière collectée.
Résolution d'une étoile double

Plus le diamètre du télescope augmente, plus la tache d'Airy diminue. Au dessus d'un certain diamètre, l'étoile apparaît double !
Crédit :
ASM/B. Mollier
 Résoudre une étoile double
Résoudre une étoile double
On cherche à observer une étoile double. Une étoile double est en fait un couple de deux étoiles. Elles peuvent être liées gravitationnellement. Elles tournent alors l'une autour de l'autre, et sont donc proches physiquement. C'est une étoile binaire. Plus de la moitié des étoiles de la galaxie vivent ainsi en couple. Albireo est un système binaire.
Cela peut aussi être uniquement un effet de perspective. Elles nous apparaissent proches l'une de l'autre, mais en fait, l'une est beaucoup plus proche de nous que la seconde. C'est un hasard si elles sont alignées. Alcor et Mizar, dans la constellation de la grande Ourse, sont un exemple d'étoiles binaires visuelles. Elles sont en fait séparées de 3 années-lumière !
Si ces étoiles sont très écartées dans le plan du ciel, pas de souci, on verra deux taches. Mais si elles sont très proches, leur tache commence à se mêler et on ne parvient plus à les distinguer l'une de l'autre.
Résolution d'une étoile double

Crédit :
ASM/B. Mollier
Ce n'est pas la peine d'augmenter le grossissement en changeant d'oculaire ! Il n'y est pour rien. La diffraction ne dépend que de la taille du télescope. Il faut donc augmenter son diamètre pour augmenter sa résolution.
 Résolution d'un télescope
Résolution d'un télescope
La résolution d'un télescope est sa capacité à distinguer de fins détails.
On définit un critère quantitatif pour calculer la résolution d'un télescope. Il s'agit du critère de Rayleigh.
L'oeil parvient à distinguer une binaire à partir du moment où le centre de la première tache est au niveau du bord de la seconde.
Critère de Rayleigh

On distingue les deux étoiles lorsque le premier anneau sombre (surligné en rouge) se superpose au centre de la seconde tache d'Airy (croix verte).
Crédit :
ASM/B. Mollier
On distingue donc une binaire à partir du moment où l'écartement 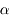 entre les deux étoiles est supérieur au rayon
entre les deux étoiles est supérieur au rayon 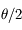 de la tache de diffraction.
de la tache de diffraction.
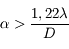
La résolution du télescope est donnée par la valeur limite 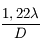 . Il est impossible de distinguer des détails plus petits que cet angle.
. Il est impossible de distinguer des détails plus petits que cet angle.
Auteur: B. Mollier
 Résolution d'un télescope
Résolution d'un télescope
L'étoile NX de la constellation des voiles (hémisphère sud) est en fait une étoile double. La séparation angulaire entre les deux composantes est de 0,7 seconde d'angle.
Constellation des voiles
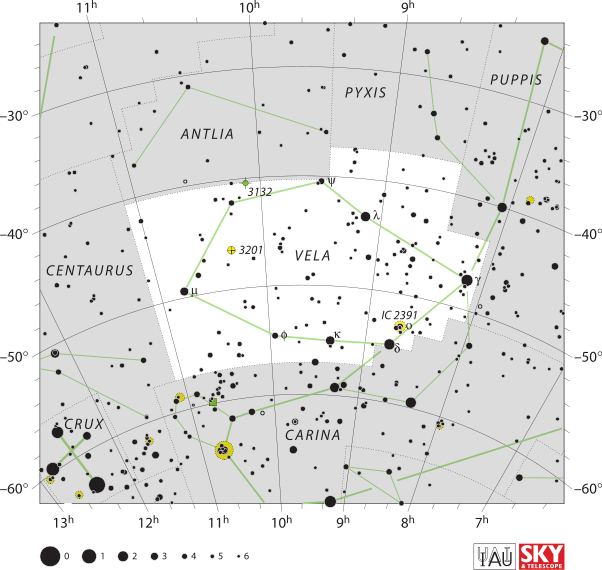
Crédit :
UAI/Sky & Telescope
nx Vel

L'étoile nx Vel.
Crédit :
Aladin
Question 1)
Quelle est la taille minimale du miroir primaire nécessaire pour pourvoir résoudre cette étoile double ? On l'observera dans le visible.
On vient de voir que la résolution d'un instrument est limitée par son diamètre. Changer de grossissement ne change pas la résolution. Que faire pour l'accroître ?
 Changer de longueur d'onde
Changer de longueur d'onde
On peut changer de longueur d'onde. En diminuant la longueur d'onde, on augmente la résolution.
Cependant, ça ne convient pas forcément à tous les cas. En effet, les techniques d'acquisition d'image ne sont pas les mêmes en radio, en infrarouge, dans le visible ou dans l'UV.
On n'observe pas non plus les mêmes objets ou phénomènes en fonction de la longueur d'onde. Aux grandes longueurs d'onde, on observe les objets froids et les phénomènes peu énergétiques. Aux petites longueurs d'onde, on observe les objets chauds et les phénomènes énergétiques.
 Augmenter le diamètre
Augmenter le diamètre
Que nous reste-t-il ? Augmenter le diamètre du télescope. Les plus grands télescopes actuels mesurent 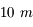 de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
Pour pouvoir voir des exoplanètes, il faut de plus grands diamètres encore. L'Europe projette de construire au Chili un télescope de 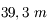 de diamètre.
de diamètre.
Les grands télescopes

L'European Extremely Large Telescope (E-ELT), avec un miroir large de
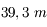
à côté des VLTs, parmi les plus grands télescopes actuels (
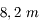
).
Crédit :
ESO
 Faisceau parallèle et système afocal
Faisceau parallèle et système afocal Image d'une plume
Image d'une plume Attention !
Attention ! Un pastille au foyer des deux lentilles
Un pastille au foyer des deux lentilles Une image !
Une image !












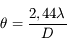
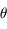 est un angle apparent.
est un angle apparent.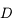 du télescope.
du télescope.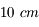 de diamètre, observant dans le visible.
de diamètre, observant dans le visible.
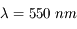 .
.
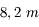 , observant dans la bande
, observant dans la bande 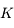 . Sera-t-il possible d'observer Bételgeuse (
. Sera-t-il possible d'observer Bételgeuse (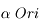 ) ?
) ?

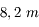 de diamètre.
de diamètre.

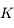 ,
, 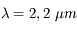 .
.
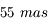



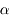 entre les deux étoiles est supérieur au rayon
entre les deux étoiles est supérieur au rayon 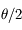 de la tache de diffraction.
de la tache de diffraction.
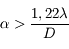
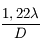 . Il est impossible de distinguer des détails plus petits que cet angle.
. Il est impossible de distinguer des détails plus petits que cet angle.


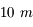 de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
de diamètre environ, et obtiennent des résolutions théoriques de l'ordre de la milliseconde d'angle (une pièce de 1 euro au Mali, vue depuis Paris).
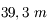 de diamètre.
de diamètre.

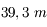 à côté des VLTs, parmi les plus grands télescopes actuels (
à côté des VLTs, parmi les plus grands télescopes actuels (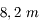 ).
).
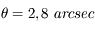
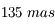 . Le diamètre de la tache d'Airy est plus grand que celui de l'étoile. Bételgeuse n'est donc pas résolue. Du moins, en bande
. Le diamètre de la tache d'Airy est plus grand que celui de l'étoile. Bételgeuse n'est donc pas résolue. Du moins, en bande 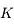 . En visible, elle le serait.
. En visible, elle le serait.
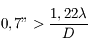
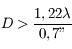
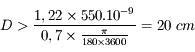
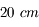 de diamètre.
de diamètre.